Introduction
This article will discuss the problem of flip binary trees in the right direction, which is clockwise. There is a prerequisite to solving this problem. You need to understand traversal in the binary tree. You can refer to this blog on coding ninjas to learn more about this.
Problem Statement
The problem states that we are given a binary tree, and we need to flip the binary tree in the right direction, i.e., The leftmost node becomes the flipped tree's root, its parent becomes its right child, and its right sibling becomes its left child in the flip process, and this should be repeated for all leftmost nodes recursively.
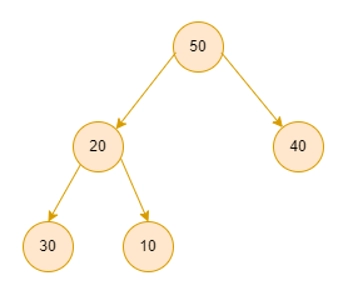
See the sample example for a better understanding of the question
Sample Examples
Input 1:
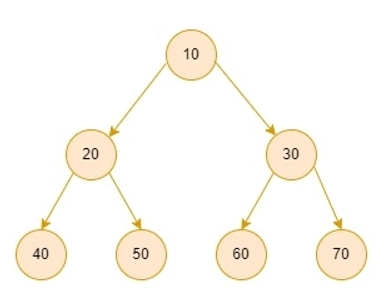
Output 1:
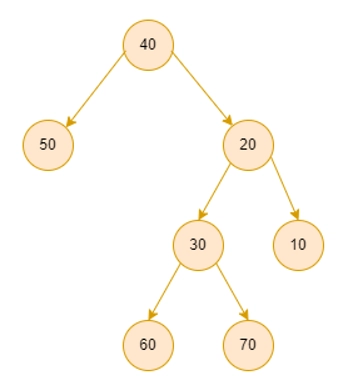
Input 2:
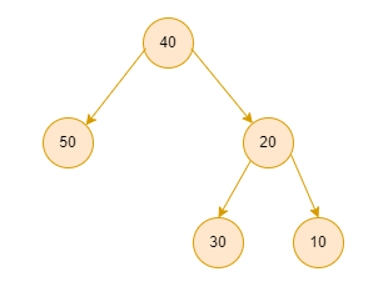
Outpu 2:
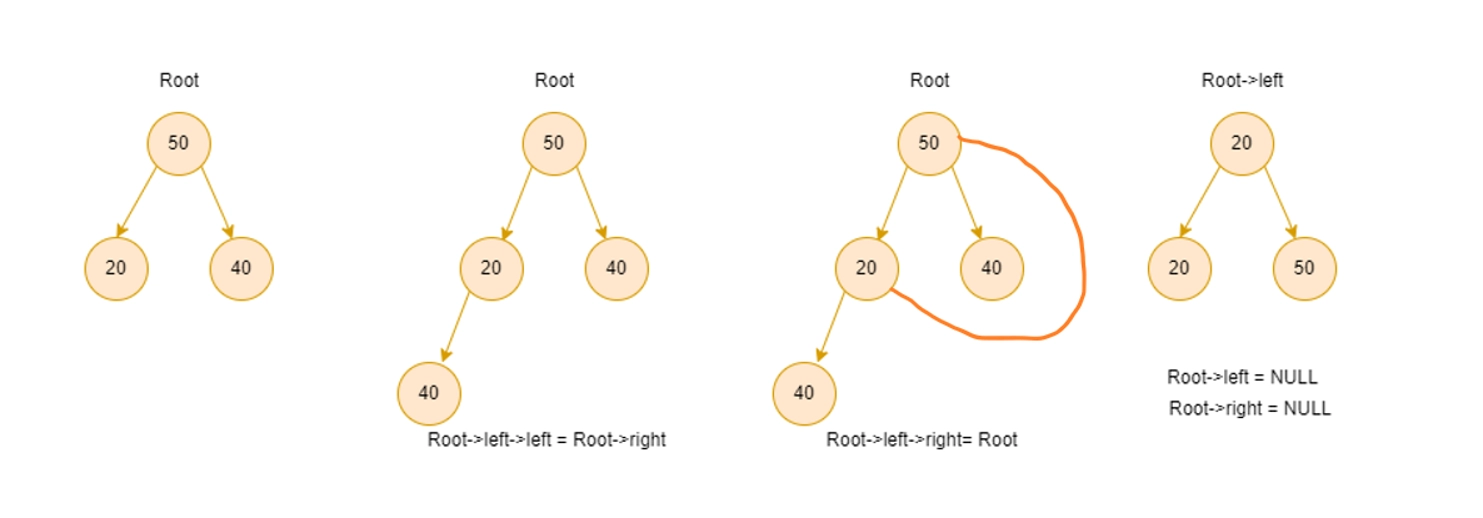
Recursive Approach
The idea is simple, main rotation code, is given as
root->left->left = root->right;
root->left->right = root;
root->left = NULL;
root->right = NULL;
To better understand this code, we will dry run on a binary tree.
Steps of Algorithm
- Take the input of the binary tree.
- Call the function FlipBinaryTree(), and pass the root of the binary tree.
- Apply the above algorithm, and finally print the level order traversal of the binary tree.
- We have finally obtained the flipped tree.
Implementation in C++
// C++ code to flip binary tree
#include <bits/stdc++.h>
using namespace std;
// binary tree class
class BinaryTreeNode
{
public:
int val;
BinaryTreeNode *left, *right;
// constructor
BinaryTreeNode(int val)
{
this->val = val;
this->left = NULL;
this->right = NULL;
}
};
BinaryTreeNode *FlipBinaryTree(BinaryTreeNode *root)
{
// if we reach the NULL node, or the tree Node, simply return the root
if (!root || (!root->left) && (!root->right))
return root;
BinaryTreeNode *flippedTree = FlipBinaryTree(root->left);
root->left->left = root->right;
root->left->right = root;
root->left = NULL;
root->right = NULL;
return flippedTree;
}
void LevelOrderTraversal(BinaryTreeNode *root)
{
// initiliazing the queue to do the level order traversal
queue<BinaryTreeNode *> q;
// pushing the root into the queue
q.push(root);
while (!q.empty())
{
int len = q.size();
while (len--)
{
BinaryTreeNode *node = q.front();
q.pop();
if (node->left)
{
q.push(node->left);
}
if (node->right)
{
q.push(node->right);
}
cout << node->val << " ";
}
cout << endl;
}
}
int main()
{
// building the binary tree
BinaryTreeNode *root = new BinaryTreeNode(50);
root->left = new BinaryTreeNode(20);
root->right = new BinaryTreeNode(40);
// printing the binary tree before calling the flip binary tree function
cout << "Printing before calling the FlipBinaryTree function" << endl;
LevelOrderTraversal(root);
root = FlipBinaryTree(root);
// printing the binary tree after calling the flip binary tree function
cout << "Printing after calling the FlipBinaryTree function" << endl;
LevelOrderTraversal(root);
cout << endl;
}
Output:
Printing before calling the FlipBinaryTree function
50
20 40
Printing after calling the FlipBinaryTree function
20
40 50
Complexity Analysis
Time Complexity: O(N)
We are only doing linear traversal of the tree, so only linear time complexity.
Space Complexity: O(1)
We are not taking any extra space to flip the binary tree.