Gate Questions on Graph Traversal - Part 2

Introduction

Graph traversal is the process of exploring each vertex in a graph. Every graph problem involves traversing in some form. It's frequently necessary to keep track of visited vertices to avoid becoming stuck in cycles. 

You can check out our Graph blogs to learn more about the Graph.

This blog covers the previous year's gate questions on Graph Traversal (related to the topic of Graph traversal).

Gate Questions on Graph Traversal

1. Let us assume a graph G which has n vertices and m edges. On Depth First Search of G, What can be the tightest upper bound on the running time? Here, We assume that the Graph is represented using an adjacency matrix. (2014 GATE Questions on Graph Traversal )

(A) O(mn)

(B) O(m+n)

(C) O(n2)

(D) O(n)
 

Answer: (C)

Explanation: When we represent a graph using an adjacency list, the Depth First Search of a graph takes O(m+n) time.

In the adjacency representation of the matrix, we represent the Graph as an "n x n" matrix. To do DFS Algorithm, We traverse the row corresponding to that vertex to find all adjacent vertices for every vertex (We traverse only the adjacent vertices of the vertex in adjacency list representation). Therefore O(n2) is the time complexity or the tightest upper bound on the running time.

 

2. Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a Data Structure for computing. ( 2014 GATE Questions on Graph Traversal )

(A) the shortest path present between every pair of vertices.

(B) the shortest path from W to every vertex in the Graph.

(C) the shortest paths from W to only those nodes that are leaves of T.

(D) the longest path in the Graph
 

Answer: (B)

Explanation: BFS always produces the shortest path from the source to all other vertices in an unweighted graph.

 

3. Suppose we execute a Depth-first search on the Graph given below, which begins at some unknown vertex. Here, it is assumed that only a recursive call to visit a vertex is made if the vertex has not been visited earlier. Then the maximum possible Recursion depth (including the initial call) is _________. (2014 GATE Questions on Graph Traversal )

                                                    

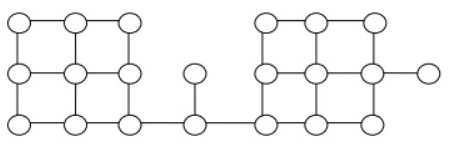
                                                                       Source: https://eduladder.com/

(A) 17

(B) 18

(C) 19

(D) 20
 

Answer: (C)

Explanation: The following diagram shows the worst-case situation where the recursion tree has maximum depth.

                                        

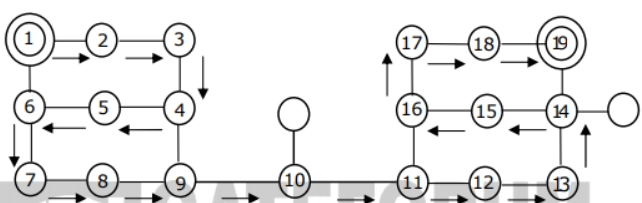
                                         Source: https://eduladder.com/

So the recursion depth is 19 (including the first node).

 

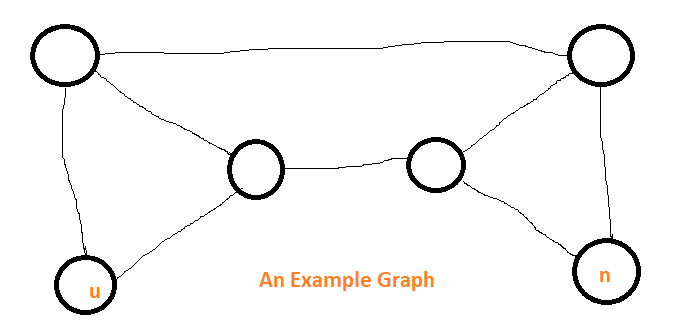
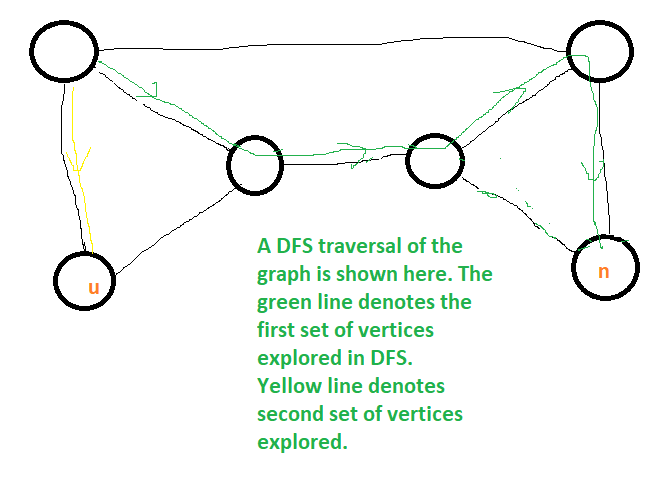
4. Let T be a depth-first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true? (2006 GATE Questions on Graph Traversal)

(A) There must exist a vertex w adjacent to both u and n in G

(B) There must exist a vertex w whose removal disconnects u and n in G

(C) There must exist a cycle in G containing u and n

(D) A cycle in G must contain u and all its neighbors in G.
 

Answer: (D)

Explanation: Below example shows that A and B are FALSE:

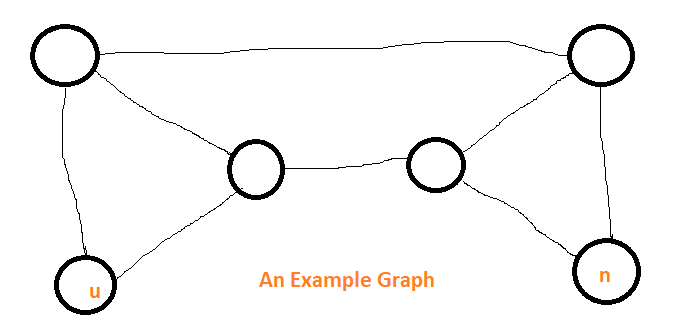
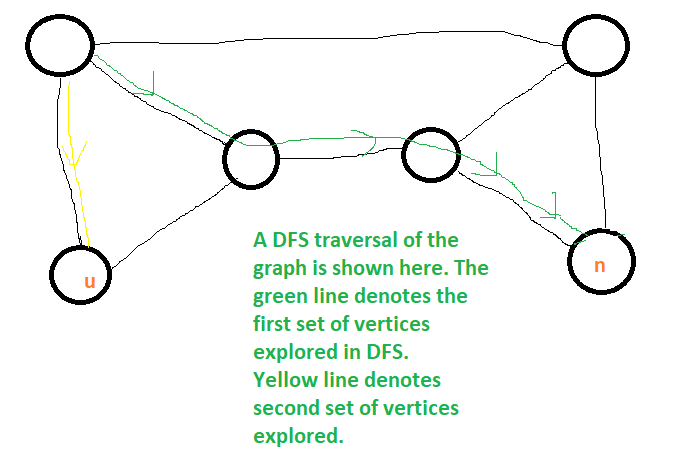
The below example shows C is false:

 

5. We marked kedges as tree edges in a depth-first traversal of a graph G with n vertices. Write the number of connected components in G 

(2000 GATE Questions on Graph Traversal )

(A) k + 1

(B) k 

(C) n – k 

(D) n – k -1 
 

Answer: (C)

Explanation: The edges that are part of the DFS tree are called Tree edges. If there are x tree edges in a tree, then x+1 vertices in the tree.

The output of DFS is a forest if the Graph is disconnected. Let us see a below simple example where Graph is disconnected.

                           

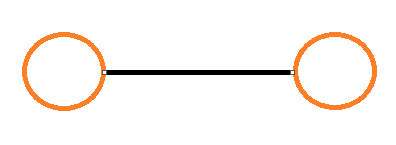
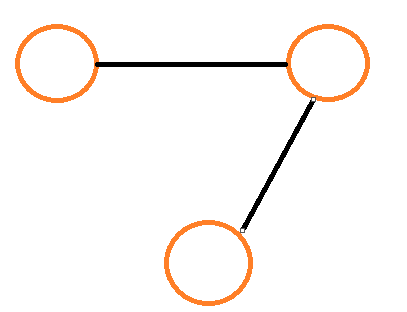
Tree Edges k = 3, Vertices n = 5, Connected Components = 2

The above example matches with the C option.

More Examples:

1) All vertices of the Graph are connected. k must be n-1. We get number of connected components = n- k = n – (n-1) = 1

2) No vertex is connected. k must be 0. We get number of connected components = n- k = n – 0 = n

 

6. Consider the following directed Graph.

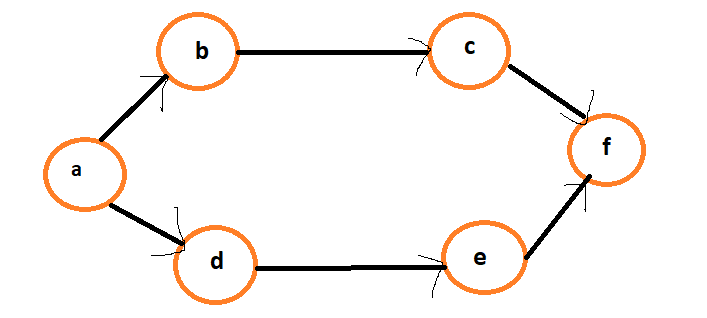
The number of different topological orderings of the vertices of the Graph is

Note: This question was asked as a Numerical Answer Type.

(A) 1

(B) 2

(C) 4

(D) 6
 

Answer: (D)

Explanation: Following are different 6 Topological Sortings

a-b-c-d-e-f

a-d-e-b-c-f

a-b-d-c-e-f

a-d-b-c-e-f

a-b-d-e-c-f

a-d-b-e-c-f
 

7. In a representation of the adjacency list of a simple graph, which is undirected, K = (V, J), each edge (g,h) has two adjacency list entries: [h] in the adjacency list of g, and [g] in the adjacency list of h. Here, g and h are called to be each other's twins. A pointer that we get from an adjacency list entry to its twin is a twin pointer. If |J| = a and |V | = b, and the size of memory does not come out as a constraint, and we want to set the twin pointer in each entry in each adjacency list, what can be the time complexity of the most efficient algorithm to do this? ( 2016 GATE Questions on Graph Traversal)

(A) Θ(b²)

(B) Θ(a+b)

(C) Θ(a²)

(D) Θ(b⁴)
 

Answer: (B)

Explanation: At first, we need to find out each node's twins. It can be done by level order traversal (i.e., BFS). The time complexity of BFS is Θ(a+b).

And you have to use a linked list for representation which is extra space (but memory size is not a constraint here).

Finally, the time complexity is Θ(a+b) to set the twin pointer.

Option (B) is correct.

 

8. Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst-case time complexity of determining if T is still an MST of the resultant Graph is

(A) Θ(∣E∣ + ∣V∣)

(B) Θ(∣E∣.∣V∣)

(C) Θ(E∣ log ∣V∣)

(D) Θ(∣V∣)
 

Answer: (D)

Explanation:

1. As T is a minimum spanning tree, we need to add a new edge to the existing spanning tree.
2. Later we need to check still T is a minimum spanning tree or not, So we need to check all vertices to see whether there is any cycle present after adding a new edge.
3. After adding a new edge, all vertices must traverse to confirm the minimum spanning tree; then, the time complexity is O(V).

Option (D) is correct.

 

9. An articulation point in a connected graph is a vertex such that removing the vertex and its incident edges disconnects the Graph into two or more connected components.

Let T be a DFS tree obtained by doing DFS in a connected undirected graph G.Which of the options written below is/are correct?

(A) Root of T can never be an articulation point in G.

(B) Root of T is an articulation point in G only if it has two or more children.

(C) A leaf of T can be an articulation point in G.

(D) If u is an articulation point in G such that x is an ancestor of u in T and y is a descendant of u in T, then all paths from x to y in G must pass through u.
 

Answer: (B) 

Explanation: How to find all articulation points? 

DFS- based-approach: 

We can prove the following properties: 

• The root of a DFS-tree is an articulation point if and only if it has at least two children. So, option A is incorrect.  
• The leaf of a DFS-tree is never articulation points. That’s why option C is incorrect.
• D is not true because it is not necessary to have a path through articulation point only. There can be a direct path from x to y in graph G.

 

10. Consider a complete binary tree with seven nodes. Let A denote the set of the first three elements obtained by performing Breadth-First Search (BFS) starting from the root. Let B represent the set of the first three elements obtained by performing a Depth-First Search (DFS) starting from the source.

The value of ∣A−B∣ is _____________ .

(A) 1

(B) 2

(C) 3

(D) 4
 

Answer: (A)

Explanation: In the case of BFS, if we draw a complete binary tree, then in Set A, we have level1+level2.

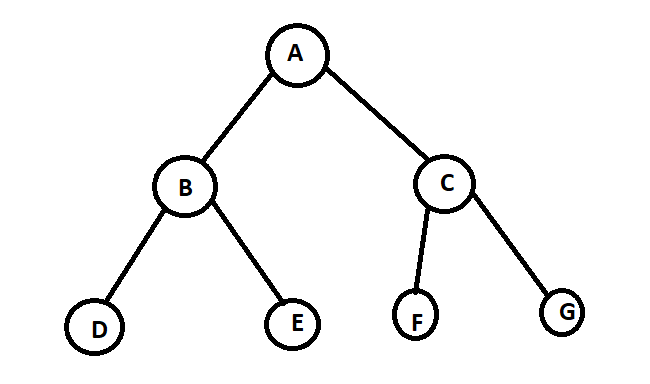
In DFS we have level1+ level 2 + level 3.

So A-B= remaining element of level 2.

For example:
In the given complete binary tree shown above, A-{A,B,C} and B-{A,B,D}. Here, A and B are sets containing the first 3 elements we get while performing bfs and dfs respectively.
In B, more than one sequence is possible, and we can choose any one of them.
So, |A-B|=|{A,B,C}-{A,B,D}|=|{C}|=1 

 

11. Consider the directed Graph given below:

 

 Which of the options written below is/are correct related to this directed Graph?

(A) A depth-first traversal starting at vertex S classifies three directed edges as back edges 

(B) The Graph does not have a topological order

(C) For each pair of vertices u and v, there is a directed path from u to v

(D) The Graph does not have a strongly connected component.
 

Answer: (A) (B)

Explanation:

(A) True, we can come back length of 3 edges. 

(B) True because of the cycle in the bottom left corner of the Graph.

(C) False, not a strongly connected graph.

(D)The Graph does have a strongly connected component; it has a cycle. 

 

12. In a directed acyclic graph with a source vertex s, the quality score of a directed path is defined as the product of the weights of the edges present in an exact way. Additionally, for a vertex v other than s, the quality score of v is the maximum among the quality scores of all the paths from s to v. The quality score of s is assumed to be 1.    

The sum of the quality scores of all vertices on the Graph shown above is _______.

(A) 929

(B) 81

(C) 729

(D) 1023
 

Answer: (A)

Explanation: Let K(V) denote the quality score of vertex V.

(S) = 1 (Given)

K(C) = 1 (S → C)

K(F) = 1 * 9 (S → C → F)

K(A) = 9 (S → A)

K(D) = 9*1 (S → A → D)

K(G) = 9 * 1 * 9 (S → A → D → G)

K(B) = 9 * 1 (S → A → B)

K(E) = 9 * 1 * 9 (S → A → D → E)

K(T) = 9*1*9*9 (S → A → D → E → T)

Sum of quality-score of all vertices' quality score is as,

= 1 + 1 + 9 + 9 + 9 + 729 + 81 + 9 + 81 

= 929

 

13. Let G=(V, E) be an undirected unweighted connected graph. The diameter of G is defined as:
diam(G) = max(u,v∈V)  {the length of the shortest path between u and v}
Let K be the adjacency matrix of G.
Define graph G₂ on the same set of vertices with adjacency matrix N, where 
N_ij ={    1 if  K_ij>0 or P_ij>0, where P=K²
              0 , otherwise 

       }
Which one of the following is true?

(A)diam(G₂) ≤ ⌈diam(G)/2⌉

(B)⌈diam(G)/2⌉ < diam(G₂) < diam(G)

(C)diam(G₂) = diam(G) 

(D)diam(G) < diam(G₂) ≤ diam(G)
 

Answer - (A)

Explanation: 

For proving that option (A) is correct, let's take an example

                                                

                                               Source: https://testbook.com/

The adjacency matrix of the graph shown above is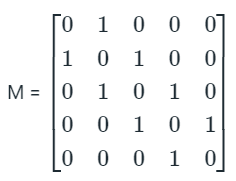

Source: https://testbook.com/

The diameter of the above graph is 4. Now,
 

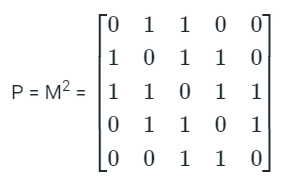
Source: https://testbook.com/

And, its graph (G2) is shown below:
 

                                                  

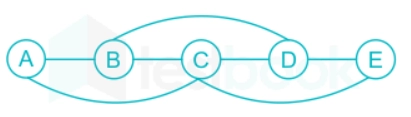
                                       Source: https://testbook.com/

The diameter of the above graph is 2.

Option D is incorrect. Let us understand this using the graph below and call it G.

                                                                             

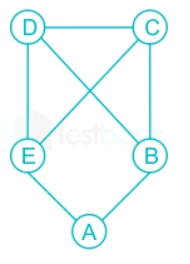
                                                                      Source: https://testbook.com/

The adjacency matrix of the graph shown above is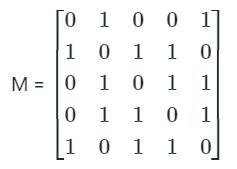

The diameter of the above graph is 2.

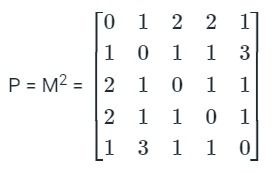
Let us call graph for matrix P, G2.

                                                        

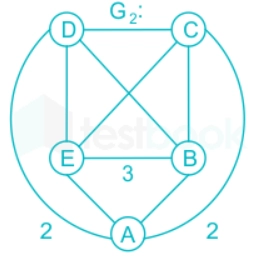
                                       Source: https://testbook.com/

The diameter of the above graph G2 is 2.

So, the diameter of G and G2 could be equal. Here, edges from G remain as it is in G2. Therefore, the diameter of G can never be less than that of G2. 

Option B is incorrect because the diameter of G and G2 could be equal also.

Option C (diam(G₂) = diam(G) ) is incorrect

 

Refer to Gate Questions on Gate Questions on Graph Traversal- 1 for more questions.