Introduction
The term "tree traversal" refers to the process of visiting each node in a tree. There is only one method to traverse a linear Data Structure like a stack, queue, or linked list. However, there are several ways to travel or visit each node in a tree. The three alternative modes of tree traversal are as follows:
- Inorder tree traversal
- Pre-order tree traversal
- Postorder tree traversal
Let us understand each traversal briefly:
-
Inorder tree traversal: A traversal approach that follows the policy, i.e., 'Left Root Right,' is an inorder tree traversal. 'Left Root Right' denotes that the root node's left subtree is read first, followed by the root node, and finally, the right subtree of the root node. The name inorder implies that the root node is located between the left and right subtrees.
-
Pre-order tree traversal: A pre-order tree traversal is a traversal approach that follows the 'Root Left Right' policy. 'Root Left Right' indicates that the tree's root node is read first, followed by the left and right subtree. The name Pre-order demonstrates that the root node would be visited first in this case.
- Postorder tree traversal: A traversal strategy that follows the policy, i.e., 'Left Right Root,' is known as a postorder tree traversal. 'Left Right Root' indicates that the root node's left subtree is read first, followed by the right subtree and the root node. The term "Postorder" implies that the tree's root node will be examined last.
Refer to Inorder, Preorder, Postorder, and Level Order tree traversals for better understanding and getting started with traversals and their approach.
Let us now go through some of the crucial gate questions on tree traversal.
Gate Questions on Tree Traversal
Below are some commonly asked gate questions on tree traversal in the GATE examination.
1. Assume the digits 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are added in that sequence into a binary search tree that is initially empty. The binary search tree follows the standard natural number ordering. What is the resulting tree's inorder traversal sequence?
a) 7 5 1 0 3 2 4 6 8 9
b) 0 2 4 3 1 6 5 9 8 7
c) 9 8 6 4 2 3 0 1 5 7
d) 1 2 3 4 5 6 7 8 9
Ans. d) 0 1 2 3 4 5 6 7 8 9
Explanation: The digits 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are added in that order into a binary search tree that was previously empty, using the standard natural number ordering. The integers sorted in ascending order always yield the inorder sequence of such a binary search tree. As a result, option (D) is the correct answer.
2. Assume that +,-, x and are left-associative, and that ^ is right-associative. The precedence order is ^, ×, +, −. The postfix expression corresponding to the infix expression "a + b × c − d ^ e ^ f " is
a) abc x + de ^ f ^ −
b) ab + c × d − e^f^
c) abc x + def ^ ^ −
d) − + a × b c^^ def
Ans. c) abc x + def ^ ^ −
Explanation:The postfix conversion of the given expression is:
a + b × c − ( d ^( e ^ f))
a + b × c − ( d ^( e f ^ ))
a + b × c − ( d e f ^ ^)
(a + (b × c)) − d e f ^ ^
(a + (b c x)) − d e f ^ ^
(a (b c x) +) − d e f ^ ^
(a b c x +) - (d e f ^ ^)
(a b c x +) - (d e f ^ ^)
a b c x + d e f ^ ^ -
Hence option (C) is the correct answer.
3. If the trees Tree-1 and Tree-2 are the ones listed below: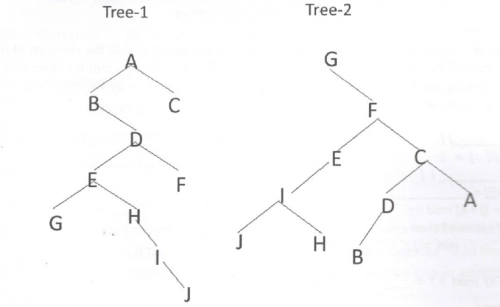
Which traversals of Tree-1 and Tree-2 will yield the same sequence, respectively?
a) Postorder, inorder
b) Postorder, preorder
c) Inorder, preorder
d) Preorder, postorder
e) None of the above
Ans. e)None of the above
Explanation:
Tree 1:
PRE ORDER: A B D E G H I J F C
IN ORDER: B G E H I J D F A C
POST ORDER: G J I H E F D B C A
Tree 2:
PRE ORDER: G F E I J H C D B A
IN ORDER: G J I H E F B D C A F
POST ORDER: J H I E B D A C F G
No order matches in both trees. Hence answer is (e).
4. FBGADCE was the outcome of traversing a tree in sequence. The tree's pre-order traversal would then result in
a) ABFGCDE
b) BFGCDEA
c) FGBDECA
d) AFGBDEC
Ans. a) ABFGCDE
Explanation: The tree's inorder traversal is as follows:
As a result, the following tree's pre-order traversal is ABFGCDE. Option (a) is the correct answer.
5. Level order Traversal of a rooted tree starting from the root can be done by performing:
a) Depth First Search
b) Root Search
c) Deep Search
d) Breadth-First Search
Ans. d) Breadth-First Search
Explanation: Level order Traversal of a rooted Tree can be done by starting from the root and performing Breadth-First Search. Hence option (d) is correct.
6. dbeafcg and abdecfg are the inorder and pre-order Traversals of a binary Tree, respectively. The postorder traversal is
a) debfagc
b) dbefcga
c) debfgca
d) dbefacg
Ans. c) debfgca
Explanation: We can identify post order by looking at pre-order (parent left right) and inorder (left parent right). It is evident from preorder(a(bdecfg)) that 'a' is the parent node (root node). We will now search for the left subtree via inorder traversal, i.e., dbe and fcg. We'll use the same procedure to discover the root node, left subtree, and right subtree of these subtrees. This will
provide us with option (c) as the correct answer.
7. Consider the following statements:
(A) A rooted tree can be traversed using a Depth-first search.
(B) To list the vertices of an ordered rooted tree, pre-order, postorder, and inorder are performed.
(C) Huffman's approach is utilized to find an optimal binary tree with specified weights.
(D) Topological sorting assigns labels to parents greater than those assigned to their children.
Which of the following statements is correct?
a) (A) and (B)
b) (C) and (D)
c) (A), (B) and (C)
d) (A), (B), (C) and (D)
Ans. d) (a), (b), (c) and (d)
Explanation: All of the given statements are true.
8. To enter a series of items 9,6,5,8,7,10 into an empty AVL tree, how many rotations are required?
a) 4
b) 3
c) 2
d) 0
Ans. b) 3
Explanation: The following diagram depicts the insertion and rotation of the various elements:
Hence a total number of 3 rotations are required. Option (b) is correct.
9. Select the corresponding prefix form of the formula (a + (b c))* ((d e)/(f + g h))
a) * +a − bc /− de − +fgh
b) * +a −bc − /de − +fgh
c) * +a − bc /− ed + −fgh
d) * +ab − c /− ed + −fgh
Ans. a) * +a − bc /− de − +fgh
Explanation: The prefix form of the expression may be written as:
= (a + (b − c))* ((d − e) / (f + g − h))
= (a + (- b c)) * ((- d e) / ( + f g - h))
= (+ a - b c) * ((- d e) / (- + f g h)
= (+ a - b c) * (/ - d e - + f g h)
= * + a - b c / - d e - + f g h
10. Assume the digits 7, 5, 1, 8, 3, 6, 0, 9, 4, 2 are entered in that sequence into a binary search tree that is originally empty. The binary search tree employs a natural number reversal order, with 9 presumed to be the smallest and 0 supposed to be the biggest. The produced binary search tree is traversed in sequence:
a) 9, 8, 7, 6, 5, 4, 3, 2, 1, 0
b) 9, 8, 6, 4, 2, 3, 0, 1, 5, 7
c) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
d) 0, 2, 4, 3, 1, 6, 5, 9, 8, 7
Ans. a) 9, 8, 7, 6, 5, 4, 3, 2, 1, 0
Explanation: The keys are always produced in ascending order when traversing a binary search tree in-order. In this question, natural numbers are ordered in reverse order, with 9 being the smallest and 0 being the greatest. As a result, the sequence will be 9, 8, 7, 6, 5, 4, 3, 2, 1, 0. As a result, option (a) is the correct answer.
11. Consider G to be a straightforward undirected graph. Let TD represent a G depth-first search tree. Let TB represent a G's breadth-first search tree. Consider the statements below. (I) About TD, no edge of G is a cross edge. (In G, a cross edge is a connection between two nodes in which neither is an ancestor of the other in TD.) (II) If u is at depth i and v is at depth j in TB for every edge (u, v) of G, then |i- j| = 1. Which of the following assertions must be true?
a) I only
b) II only
c) Both I and II
d) Neither I nor II
Ans. a) I only
Explanation: Tree, forward, back, and cross edges are the four types of edges that may be produced in DFS. Forward and back edges are the same thing in an undirected connected graph. In a graph, a cross edge connects one vertex v to another vertex u, where u is neither an ancestor nor a descendant of v. As a result, a cross edge is not feasible in an undirected graph. As a result, assertion (I) is true. Take a counterexample of a complete graph with three vertices, such as K3 with XYZ, where X is the source, and Y and Z are on the same level, for the assertion (II). In BFS, there is also an edge connecting vertices Y and Z, i.e. |i-j| = 0 != 1. As a result, the assertion was proven to be untrue. Option (a) is the correct answer.
For more GATE questions on tree traversals, refer to our Gate Questions on Tree Traversal: Part 2 and Gate Questions on Tree Traversal: Part 3.
Check out this problem - Diameter Of Binary Tree




