Introduction
In Data Structure, an array is a variable that can store more than one value in a single variable without declaring separate variables for each value. And, Sorting is a technique for ordering the elements in a list by their proper ranks, i.e., ascending order or descending order.
In this article, we will discuss how to generate all possible sorted arrays from alternate elements of two given sorted arrays and we will use the concept of arrays and sorting. So, without wasting your time let's start!!
Problem Statement
Suppose you have two arrays named Array X and Array Y. Now the problem statement is asking to find all the possible sorted arrays so that the values should be arranged alternatively from the two given different arrays, and the resultant array should end with an element from Y.
Sample Example
Suppose there are two arrays of the name ArrX and ArrY. The values in given arrays are:
Input:
ArrX[] = {8, 11, 65}
ArrY[] = {10, 16, 26}
Output:
8 10
8 10 11 16
8 10 11 26
8 16
8 26
11 16
11 26Approach
The Approach is simple and easy to understand. Suppose we have two given arrays, ArrX and ArrY, and a resultant array, ArrRes. We will use Recursion in BFA for the problem mentioned above:
-
Take two sorted arrays and an empty or resultant array named ArrX, ArrY, and ArrRes.
-
Check if the resultant array is not empty, and return the resultant array.
-
If it is empty, copy the first value of ArrX in ArrRes.
-
Now, compare the first element of ArrX to the first element of ArrY.
-
If the first element of ArrX is smaller than the first element of ArrY, copy both arrays' values to the resultant array and return the resultant array ArrRes.
-
Now, check the second element of both arrays. If they are also sorted(the value of ArrX is smaller than the value of ArrY), then put the values(X[0], Y[0], X[1], Y[1]) in ArrRes and return the resultant array. We have done this as they are adjacent to each other.
- Similarly, using recursion, compare each element from both arrays and if they are sorted, copy them to the resultant array and return the values in ArrRes.
Implementation
class MySortedArray
{
public static void SortedArray(int ArrX[], int ArrY[], int output[], int i, int j, int len_Y, int len_X, int length, boolean flag)
{
if (flag)
{
if (length!=0)
printArray(output, length+1);
for (int k = i; k < len_Y; k++)
{
if (length==0)
{
output[length] = ArrX [k];
SortedArray(ArrX, ArrY, output, k+1, j, len_Y, len_X, length, !flag);
}
else
{
if (ArrX [k] > output[length])
{
output[length+1] = ArrX [k];
SortedArray(ArrX, ArrY, output, k+1, j, len_Y, len_X, length+1, !flag);
}
}
}
}
else
{
for (int l = j; l < len_X; l++)
{
if (ArrY[l] > output[length])
{
output[length+1] = ArrY[l];
SortedArray(ArrX, ArrY, output, i, l+1, len_Y, len_X, length+1, !flag);
}
}
}
}
public static void generate(int ArrX [], int ArrY[], int len_Y, int len_X)
{
int output[]=new int[len_Y+len_X ];
SortedArray(ArrX, ArrY, output, 0, 0, len_Y, len_X, 0, true);
}
public static void printArray(int arr[], int len_X)
{
for (int i = 0; i < len_X ; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void main(String [] args)
{
int ArrX[] = {8, 11, 65};
int ArrY[] = {10, 16, 26};
int len_X = ArrX.length;
int len_Y = ArrY.length;
generate(ArrX, ArrY, len_X, len_Y);
}
}
Output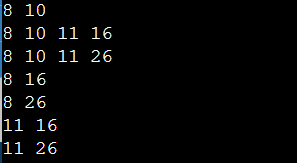
Time Complexity
The time complexity of the given problem is O(N^2), where N is the size of arrays. If the size of both arrays is not equal, then the time complexity of the stated problem will be O(N1^2 + N2^2), where N1 and N2 are the sizes of the array.
Space Complexity
The space complexity for the given problem is O(M+N), where M and N are the sizes of both arrays.
Also see, Rabin Karp Algorithm





