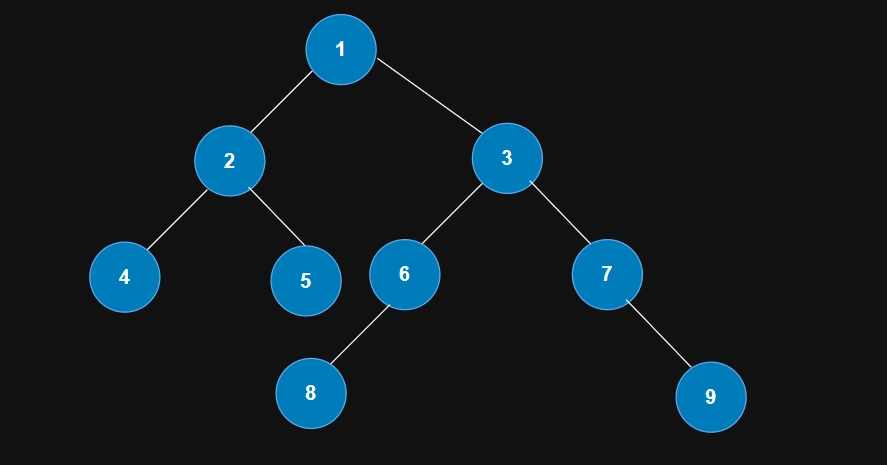
Approach
The approach for the above problem is quite simple and straightforward. The goal is to traverse the tree in a preorder manner and store every encountered node in a vector along the current path from the root to the leaf. If a leaf node is encountered, print all nodes in the vector. Then, we will have all the root-to-leaf paths.
Algorithm
1. To store the current root to leaf path, use a path array path[].
2. In a top-down manner, traverse starting from the root to all the leaf nodes.
3. Store the data of all nodes in the current path in the array path[] while traversing.
4. Print the path array whenever we reach a leaf node.
Implementation in C++
#include <iostream>
#include <vector>
using namespace std;
// Declaring a binary tree node
struct Node
{
int data;
Node *l, *r;
Node(int data)
{
this->data = data;
this->l = this->r = nullptr;
}
};
// Checking a node is a leaf node or not
bool isLeafPath(Node* node) {
return (node->l == nullptr && node->r == nullptr);
}
// Function to find paths from the root node to each leaf node
void printPaths(Node* node, vector<int> &path)
{
// base case
if (node == nullptr) {
return;
}
path.push_back(node->data);
if (isLeafPath(node))
{
for (int data: path) {
cout << data << " ";
}
cout << endl;
}
printPaths(node->l, path);
printPaths(node->r, path);
path.pop_back();
}
// function to print root-to-leaf paths
void printPaths(Node* node)
{
vector<int> path;
printPaths(node, path);
}
int main()
{
Node* root = new Node(1);
root->l = new Node(2);
root->r = new Node(3);
root->l->l = new Node(4);
root->l->r = new Node(5);
root->r->l = new Node(6);
root->r->r = new Node(7);
root->r->l->l = new Node(8);
root->r->r->r = new Node(9);
cout<<"The root-to-leaf paths are: "<<endl;
printPaths(root);
return 0;
}

You can also try this code with Online C++ Compiler
Output
The paths from the root node to each leaf node of the tree are:
1 2 4
1 2 5
1 3 6 8
1 3 7 9
Time Complexity
The Time Complexity of the given approach is O(n), where n is the number of nodes as we traverse through each tree node only once to print root-to-leaf paths.
Space Complexity
The program’s Space Complexity will be O(h), where ‘h’ is the height of the binary tree as the path that array formed to print the root-to-leaf paths is equal to the height of the tree.
Frequently Asked Questions
What is the height of the tree?
The height of a node is defined as the number of edges connecting it to the leaf node along the longest path.
What is an AVL tree?
A binary search tree, or AVL tree, is a form of the binary search tree. In addition to all the other properties of binary search trees, AVL trees have the property of dynamic self-balancing.
Can a tree have a height of 0?
Yes, The height of a (rooted) tree with only one node (the root) is zero.
What is the Balance Factor?
A binary tree's balancing factor is the height difference between its two subtrees (hR - hL).
Conclusion
This article extensively discussed the problem of printing all the root-to-leaf paths of the given binary tree and its time and space complexities.
Cheers, you have reached the end. Hope you liked the blog and it has added some knowledge to your life. Please look at these similar topics to learn more: Binary Tree, Binary Search Tree, Binary Tree to BST, and All Binary Trees.
Refer to our Coding Ninjas Studio Guided Path to learn Data Structures and Algorithms, Competitive Programming, JavaScript, System Design, and even more! You can also check out the mock test series and participate in the contests hosted by Coding Ninjas Studio! But say you're just starting and want to learn about questions posed by tech titans like Amazon, Microsoft, Uber, and so on. In such a case, for placement preparations, you can also look at the problems, interview experiences, and interview bundle.
You should also consider our premium courses to offer your career advantage over others!
Please upvote our blogs if you find them useful and exciting!
Happy Coding!