Introduction
Graph data structures are among the most important and exciting topics to learn in computer science because of their usage in several real-world applications like in Google Maps, Circuit Designing, etc.
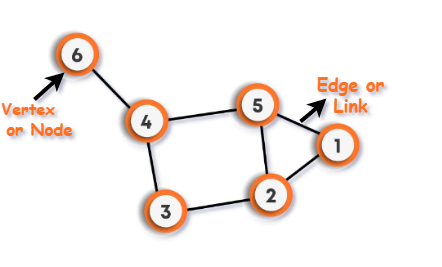
Formally, A graph is a non-linear Data Structure containing nodes and links between them called edges.
.
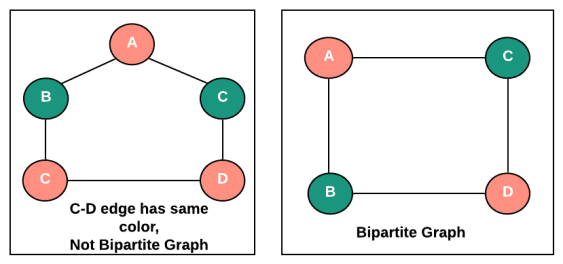
In this article, we will see various graph terminologies, important theorems, and some special simple graphs.
Before we proceed, have you considered how we might represent these graphs?
There are two common ways we use to represent graphs, and the two ways are as follows :
- Using Adjacency Matrix
- Using Adjacency List
To learn more about the graph representation, visit the blog here.
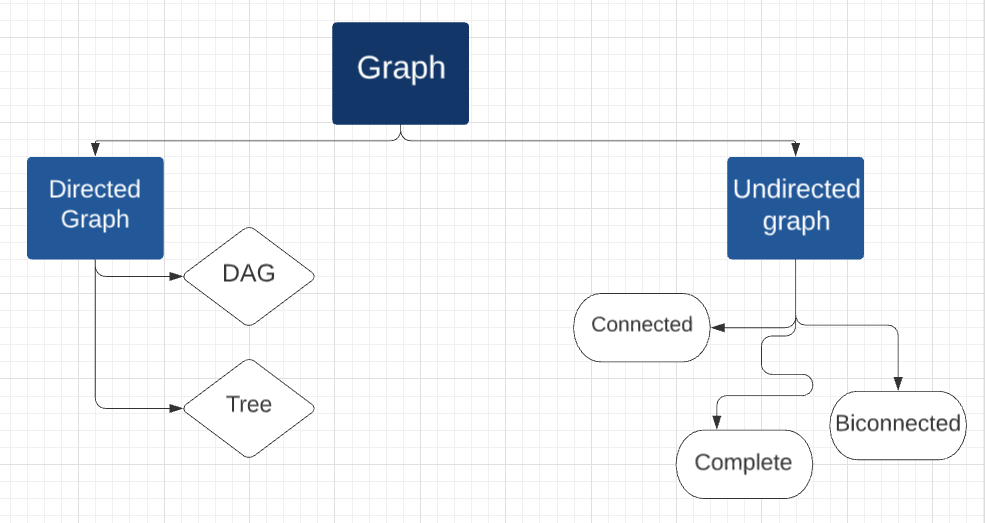
Terminologies in Graph
Basic graph terminology, such as vertices, edges, directed and undirected edges, and so on, have already been covered in this blog. Some additional terms to describe the properties of graphs are as follows:
- Degree of a node: The degree of a node is the number of edges incident to that node. The degree of vertex u is denoted by deg(u).
Note: A vertex with a degree 0 is called isolated. The one with degree 1 is called a pendant.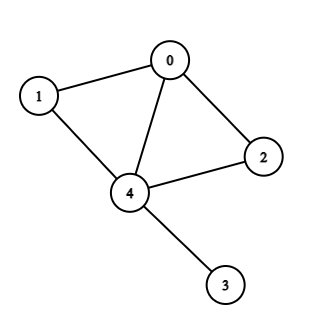
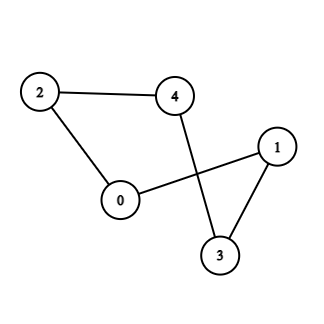
The degree of the nodes in the above-undirected graph is given in the table below:
| Node | Degree |
| deg(0) | 3 |
| deg(1) | 2 |
| deg(2) | 2 |
| deg(3) | 1 |
| deg(4) | 4 |
- Indegree: denoted by deg-(v) is the number of edges incident to that node.
- Outdegree: denoted by deg+(v) is the number of edges outgoing from that node. The degree of a node is the sum of outdegree and indegree.
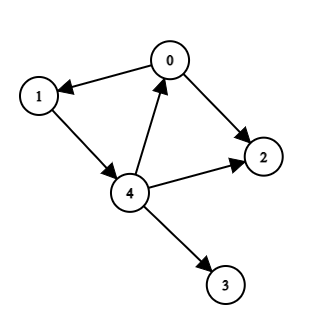
The indegree and outdegree of the above graph are given in the table below:
| Node | Indegree |
| deg-(0) | 1 |
| deg-(1) | 1 |
| deg-(2) | 2 |
| deg-(3) | 1 |
| deg-(4) | 1 |
| Node | Out |
| deg+(0) | 2 |
| deg+(1) | 1 |
| deg+(2) | 0 |
| deg+(3) | 0 |
| deg+(4) | 2 |
2. Path: A path is defined as a sequence of nodes in the order we're visiting them. The order in which we go from node 'u' to reach v is known as path.
Note: No node should be repeated in the path ever, except when the source and destination are the same.
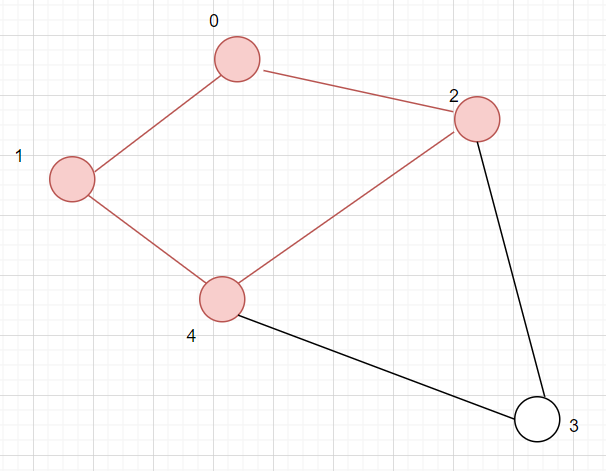
Here, 2 -> 4 -> 0 -> 1 is a path from vertex 2 to 1.
3. Walk: A walk is a sequence of vertices and edges of a graph. In a walk, vertices and edges can be repeated.
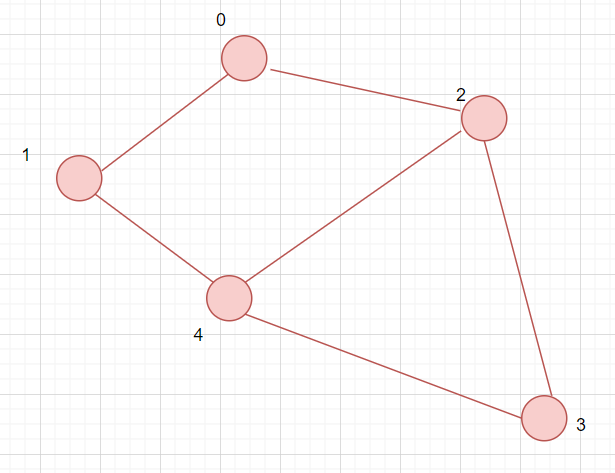
Here, 1 -> 0 -> 2 -> 3 -> 2 -> 4 is a walk.
- Open walk: A walk is an open walk when the initial and final vertices are different.
For example: In the above graph, 1 -> 0 -> 2 -> 4 -> 3 is an open walk.
- Closed walk: A walk is an open walk when the initial and final vertices are the same.
For example: In the above graph, 1 -> 0 -> 2 -> 4 ->1 is a closed walk.
4. Trail: An open walk in which no edge is repeated is called a trail.
Note: Vertex can be repeated in a trail.

In the above example, 1 -> 0 -> 2 -> 3 -> 4 -> 2 is a trail. Here, vertex 2 is repeated but not any edge.
5. Circuit: A graph traversal that is closed and in which there is no edge repetition, but vertex repetition can occur called a circuit.

In the above example, 1 -> 0 -> 2 -> 3 -> 4 ->1 is a circuit. Here, vertex 1 is repeated but not any edge.