Greedy Algorithm in Graph Theory

Introduction

In graph theory, greedy algorithms play a crucial role in solving a variety of optimization problems efficiently. These algorithms make a series of choices, each of which looks best at the moment, with the goal of finding the optimal solution. Greedy algorithms are particularly effective for problems where making local optimal choices leads to a globally optimal solution. This article explores the application of greedy algorithms in graph theory.

What are Greedy Algorithms

Greedy algorithms are a class of algorithms that make a sequence of choices, each of which is the best or most optimal at that specific step, with the hope that these local choices will lead to a globally optimal solution. The key idea behind greedy algorithms is to make the "greedy" choice that seems best at the moment, without reconsidering previous decisions.

Characteristics of the Greedy Method

Greedy-Choice Property: At each step, the algorithm makes the best choice from the current options.
Optimal Substructure: A problem has an optimal substructure if an optimal solution to the problem contains an optimal solution to its subproblems.
Irrevocable Decisions: Once a decision is made, it cannot be changed or undone; the algorithm moves forward without revisiting previous steps.
Local to Global Approach: The algorithm builds a solution by making a series of locally optimal choices to find a globally optimal solution.
Efficiency: Greedy algorithms are typically more efficient regarding time and space complexity, making them suitable for large-scale problems.

Steps for Creating a Greedy Algorithm

Identify the Problem: Clearly define the problem you want to solve and determine if it can be approached using a greedy strategy.
Determine the Greedy Choice: Identify the best choice you can make at each step that seems to lead towards an optimal solution.
Prove the Greedy-Choice Property: Ensure that making the greedy choice at each step will lead to an optimal solution for the overall problem.
Establish Optimal Substructure: Verify that the problem has an optimal substructure, meaning an optimal solution to the main problem can be constructed from optimal solutions to its subproblems.
Implement the Algorithm: Translate the greedy strategy into a step-by-step algorithm and implement it in your preferred programming language.
Test the Algorithm: Test your greedy algorithm with various inputs to ensure it provides the correct and optimal solution.

Real-life example for Greedy Algorithms:

Consider a boy named Ram. He has a box which can accommodate at most 3 chocolates. His friend offers him 4 chocolates namely A, B, C and D of Rs.10, Rs.20, Rs.30 and Rs.40 respectively. Ram can only choose as many chocolates as the box can accommodate. This means Ram can choose 3 chocolates at most.

Which 3 chocolates should he choose so that his profit is maximized??? Also, he can make only 3 choices. In each choice, he can pick one chocolate. Yes, you got it right… He should choose B, C, and D.

Let’s try to understand this situation algorithmically by applying the greedy approach. Initially, Ram’s box is empty and his friend has four chocolates.

Step 1: According to the definition of a greedy algorithm, Ram will choose the chocolate that will offer him the most immediate and largest profit. In this case, Ram will choose D because he will get a profit of Rs.40 which is greater than the profit made by choosing any other chocolate.

Step 2: Now Ram’s box can accommodate 2 more chocolates. Ram has to choose 2 chocolates out of 3 such that “immediate” profit is maximized. He will choose C because of the same reason stated in step 1.

Step 3: Now Ram’s box has the capacity to accommodate only 1 chocolate. Ram has to choose 1 chocolate out of 2 such that “immediate” profit is maximized. He will choose B because of the same reason stated in step 1.

Now Ram’s box is full and profit is also maximised. You can try various combinations of choosing 3 chocolates out of the four chocolates in a given scenario and you will find that the profit is maximum for the above-mentioned combination with the least number of steps. So, In this case, our objective function was the profit that had to be maximized.

Some of the standard problems that can be solved using the greedy algorithm include the famous fractional knapsack problem, job sequencing problem, etc. Here, we will look at various graph greedy algorithms that are greedy algorithms and Data Structure.

Greedy Algorithms in Graphs

Spanning Tree and Minimum Spanning Tree

In terms of graph theory, a spanning tree T of an undirected graph G is a tree that includes all of the nodes of the graph G. The tree T is also a subgraph of the given graph G. A single graph can have more than one spanning tree.

A minimum spanning tree (MST) for a graph is a spanning tree with a weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.

If a graph G has V number of vertices, its minimum spanning tree will have (V-1) number of edges. The two famous algorithms for finding the minimum spanning tree for a given graph.

They are Prim’s algorithm and Kruskal’s algorithm. Both of these are discussed in the following sections.

Kruskal’s Algorithm

Kruskal’s algorithm is used to find the minimum spanning tree for a given graph G.

The algorithm is as follows-

Sort the edges of the graph in a non-decreasing order for their weights
Pick the edge with the smallest weight. Check if the edge forms a cycle with the MST constructed so far. If it forms a cycle, discard it, else include it in the MST.
Repeat step 2 till there is (V-1) number of edges in the graph (and all vertices are covered). Here, V represents the number of vertices in graph G.

Let’s understand the workings of the above algorithm with an example.

Consider the graph:

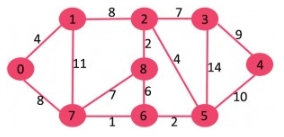
Kruskal’s Algorithm

It has nine vertices and 14 edges. So, its MST will have (9-1) i.e eight edges. After sorting the edges according to increasing order of their weights, we get the following:

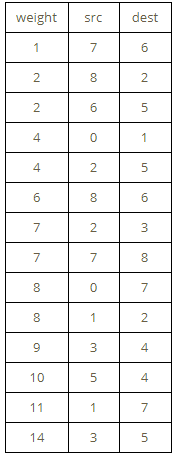
Kruskal’s Algorithm Table

Here, src refers to the source vertex of a given edge, dest refers to the destination vertex of a given edge and weight refers to the weight of the given edge. Now let’s implement Kruskal’s algorithm as stated above.

Pick all edges one by one from the sorted list of edges.

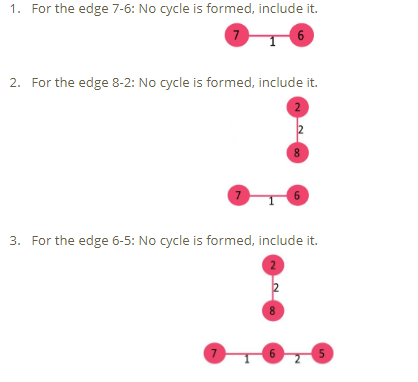
Kruskal’s Algorithm-1

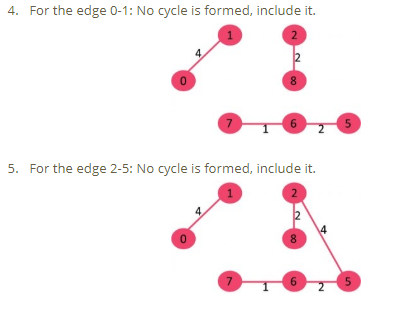
Kruskal’s Algorithm-2

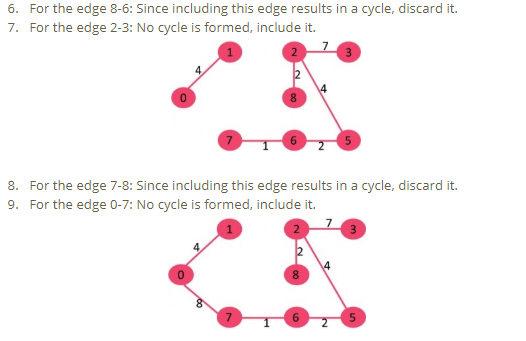
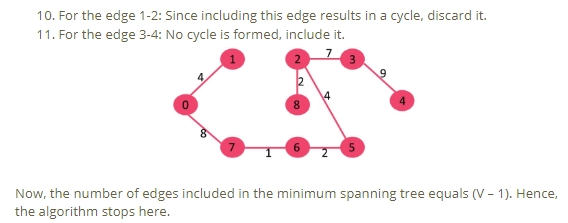
Kruskal’s Algorithm-3

You can refer to Coding Ninjas courses for the best in-depth explanations for understanding these concepts.

Time Complexity of Kruskal’s algorithm:

The time complexity for Kruskal’s algorithm is O(ElogE) or O(ElogV). Here, E and V represent the number of edges and vertices in the given graph respectively. Sorting of all the edges has the complexity O(ElogE). After sorting, we apply the find-union algorithm for each edge. The find and union operations have the worst-case time complexity is O(LogV). So overall complexity becomes O(ElogE + ElogV). The value of E can be V^2 in the worst case. Hence, O(LogV) is O(LogE) become the same. Therefore, the overall worst-case time complexity becomes O(ElogE) or O(ElogV).

Read More - Time Complexity of Sorting Algorithms

Prim’s Algorithm

Like Kruskal’s algorithm, Prim’s algorithm is also used to find the minimum spanning tree of a given graph. In Kruskal’s algorithm, we were adding an edge to an existing MST. But, Here, we will add a vertex to the existing (growing) MST.

Maintain two disjoint sets of vertices: One set will contain the vertices that are a part of the growing spanning tree. The other set will contain the vertices that are not a part of the growing spanning tree.
Select the cheapest vertex that is connected to the growing spanning tree. This vertex should not be there in the already growing spanning tree. Add this vertex into the growing spanning tree. This can be achieved using Priority Queues. Insert the vertices, that are connected to the growing spanning tree, into the Priority Queue.
Check for cycles: In order to check for cycles, mark the nodes which have been already selected. In the priority queue, insert only those nodes that are not marked.

In Prim’s Algorithm, we have to start with an arbitrary node and mark it. In each iteration, we will mark a new vertex that is adjacent to the one that we have already marked. Prim’s algorithm being a greedy algorithm, it will select the cheapest edge and mark the vertex.

Get a Head start on Summer with a programming checklist by Coding Ninjas 2021.

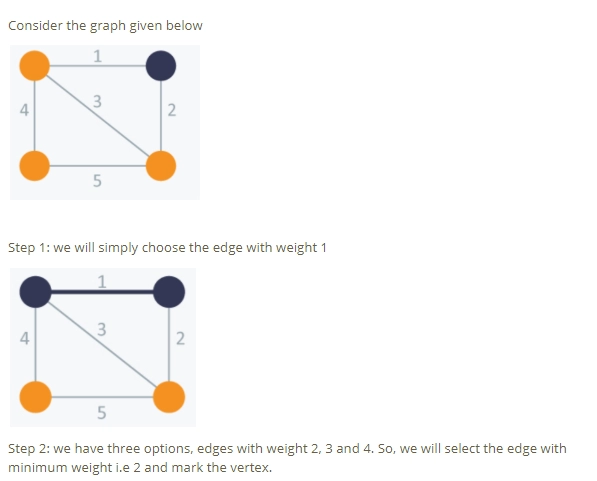
Prim’s Algorithm-1

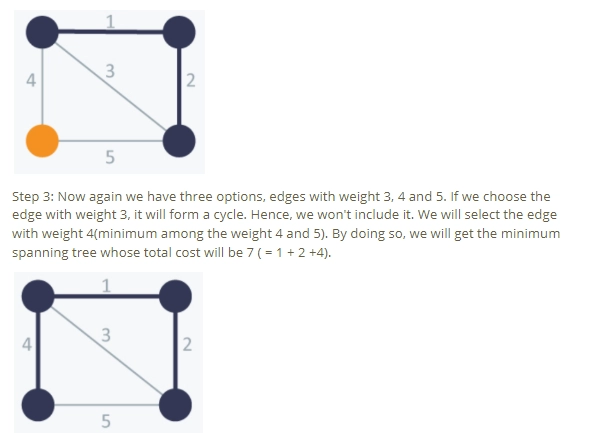
Prim’s Algorithm-2

Need help with the Google Kickstart Exams, join our free trials courses to practice exam problems at Coding Ninjas Studio only.

Time Complexity:

The worst case time complexity of the Prim’s Algorithm is O((V+E)logV). This is because each vertex is inserted in the priority queue only once and insertion in priority queue takes logarithmic time.

Applications of Minimum Spanning Trees:

Direct application in the design of networks (a network of computers, cellular networks road networks, etc.)
Handwriting Recognition
Cluster analysis
Image segmentation

Also Read - Kadanes Algorithm

Applications of Greedy Algorithm

Minimum Spanning Tree (MST): Algorithms like Kruskal’s and Prim’s are used to find the MST of a graph, which connects all vertices with the minimum total edge weight.
Shortest Path Problem: Dijkstra’s algorithm finds the shortest path from a source vertex to all other vertices in a weighted graph with non-negative weights.
Huffman Coding: Used in data compression, Huffman coding builds an optimal prefix-free binary code based on the frequency of characters.
Activity Selection Problem: Determines the maximum number of activities that can be scheduled without overlap, based on start and end times.
Fractional Knapsack Problem: Solves the problem of maximizing the total value in a knapsack with fractional item inclusion allowed, based on item value-to-weight ratios.
Job Sequencing Problem: Schedules jobs to maximize the total profit, considering deadlines and job durations, with a focus on selecting the most profitable jobs.

Disadvantages/Limitations of Using a Greedy Algorithm

Not Always Optimal: Greedy algorithms do not guarantee an optimal solution for all problems; they work well only if the problem satisfies the greedy-choice property and optimal substructure.
Limited Applicability: Some problems may not be suited for a greedy approach, requiring other algorithms like dynamic programming or backtracking to find optimal solutions.
Lack of Global View: Greedy algorithms make decisions based on local information without considering the global context, which can lead to suboptimal solutions.
Possible Solution Infeasibility: In some cases, a greedy algorithm may produce a solution that is feasible but not the best or required solution for the problem.
Difficulty in Proving Optimality: Proving that a greedy solution is optimal can be challenging and may require a deep understanding of the problem's structure and properties.

Frequently Asked Questions

Why are greedy algorithms used?

Greedy algorithm helps to arrive at the most optimal solution in the best possible time.

List a few characteristics of Greedy algorithms.

Greedy algorithm is a simple method to solve the problem and derive an optimal solution at each step. These algorithms are fast and more intuitive compared to any other algorithms.

Name some popular greedy algorithms.

Some popular greedy algorithms are prim's algorithm, Kruskal's algorithm, Dijkstra's algorithm, and Knapsack problem.

Conclusion

In this article, we have discussed the Greedy Algorithm in Graph Theory. Greedy algorithms offer a powerful approach for solving a variety of optimization problems in graph theory by making a series of locally optimal choices. Their efficiency and simplicity make them particularly effective for problems like finding minimum spanning trees, shortest paths, and job sequencing.