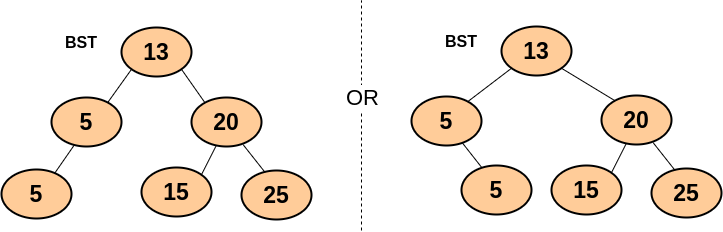
Approach #1
We have two different methods2️⃣,
🥇The first method is to store the duplicate element in the left subtree which means the new definition of a binary tree will be
Left node <= Root node < Right node
🥈 The second method is to store the duplicate elements in the right subtree which lays down the following definition.
Left node< Root node <= Right node
We’ll be following the first method for solving the problem
Algorithm
INSERT(ROOT, VAL):
IF ROOT IS NULL:
return new NODE(val);
if VAL > ROOT:
ROOT->right = INSERT(ROOT->right, VAL);
else if VAL <= ROOT->data:
ROOT->left = INSERT(ROOT->left, VAL);
return ROOT;
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
// Node
class Node
{
public:
int data;
Node *left, *right;
Node(int val)
{
data = val;
left = right = nullptr;
}
};
// function to print inorder traversal of tree
void inorder(Node *root)
{
if (!root)
return;
inorder(root->left);
cout << root->data << ' ';
inorder(root->right);
}
// insertion operation
Node* insert(Node *root, int val)
{
if (!root)
{
// Inserting the first node, if root is null.
return new Node(val);
}
// Inserting
if (val > root->data)
{
root->right = insert(root->right, val);
}
else if (val <= root->data)
{
root->left = insert(root->left, val);
}
return root;
}
// main function
int main()
{
// Inserting value in tree
Node *root = nullptr;
root = insert(root, 13);
root = insert(root, 5);
root = insert(root, 20);
root = insert(root, 15);
root = insert(root, 25);
cout << "Inorder Traversal before inserting: ";
inorder(root);
// inserting new element
insert(root, 5);
cout << "\nInorder Traversal after inserting: ";
inorder(root);
cout << endl;
return 0;
}

You can also try this code with Online C++ Compiler
Output
Inorder Traversal before inserting: 5 13 15 20 25
Inorder Traversal after inserting: 5 5 13 15 20 25
Time Complexity
⏱️ Insertion in the binary search tree takes O(h) time, where h is the height of the Binary Search Tree.
Space Complexity
🔧Constant extra space is used. So, the space complexity of our program is O(1).
🌟 It is completely fine to store the elements either way but we are obliged with a much more efficient method of storing the duplicate elements inside a binary search tree. Let us see how.
Approach #2
💥 As we know that we will be having duplicate elements, We will insert all the elements in a similar manner as we do it in a binary search tree and once any duplicate element comes, we will increment the count of the number.
FOR EXAMPLE
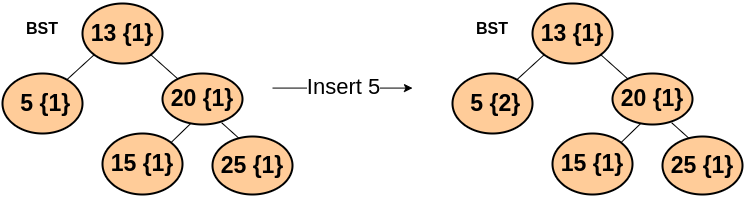
Algorithm
INSERT(ROOT, VAL):
IF ROOT IS NULL:
return new NODE(val);
if VAL > ROOT:
ROOT->right = INSERT(ROOT->right, VAL);
else if VAL < ROOT->data:
ROOT->left = INSERT(ROOT->left, VAL);
else if VAL == ROOT:
ROOT->count = ROOT->count + 1;
return ROOT;
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
// Node
class Node
{
public:
int data;
int count;
Node *left, *right;
Node(int val)
{
data = val;
count = 1;
left = right = nullptr;
}
};
// function to print inorder traversal of tree
void inorder(Node *root)
{
if (!root)
return;
inorder(root->left);
// as we are storing the count of the node
for(int i= 0; i < root->count; i++) cout << root->data << ' ';
inorder(root->right);
}
// insertion operation
Node* insert(Node *root, int val)
{
if (!root)
{
// Inserting the first node, if root is null.
return new Node(val);
}
// Inserting
if (val > root->data)
{
root->right = insert(root->right, val);
}
else if (val < root->data)
{
root->left = insert(root->left, val);
}
// incrementing the count if duplicate node is found
else if(val == root->data){
root->count++;
}
return root;
}
// main function
int main()
{
// Inserting value in tree
Node *root = nullptr;
root = insert(root, 13);
root = insert(root, 5);
root = insert(root, 20);
root = insert(root, 15);
root = insert(root, 25);
cout << "Inorder Traversal before inserting: ";
inorder(root);
// inserting new element
insert(root, 5);
cout << "\nInorder Traversal after inserting: ";
inorder(root);
cout << endl;
return 0;
}

You can also try this code with Online C++ Compiler
Output
Inorder Traversal before inserting: 5 13 15 20 25
Inorder Traversal after inserting: 5 5 13 15 20 25
Time Complexity
⏱️ The time complexity of this approach is the same as the above approach which is O(h), Where h is the height of the BST.
Space Complexity
🔧 Constant extra space is used. So, the space complexity of our program is O(1).
Check out this problem - Largest BST In Binary Tree
Frequently Asked Questions
What is a binary search tree?
A Binary search tree is a type of binary tree in which all the nodes having lesser values than the root node are kept on the left subtree, and similarly, the values greater than the root node are kept on the right subtree.
How many nodes are there in a complete binary tree?
If n is the total number of nodes, and h is the height of the tree then, the total number of nodes in the complete binary tree is 2^h – 1.
Describe the time complexity of making insertions in a binary search tree.
In general, the time complexity of making insertions in a binary search is O(h), where h is the height of the BST. In case the tree is not balanced then the time complexity of insertion would be O(N), Where N is the number of nodes.
Conclusion
In this article, we have extensively discussed a solution to handle the duplicate value in BST. We have seen two different approaches to handle duplicates in Binary Search Tree.
If you think this blog has helped you enhance your knowledge about the above question, and if you want to learn more, check out our articles.
And many more on our Website.
Visit our website to read more such blogs. Make sure you enrol in our courses, take mock tests, solve problems, and interview puzzles. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations.
Please upvote our blog to help other ninjas grow.
Happy Learning!