Height of a Binary Tree in Data Structure

Introduction

A binary tree is an important data structure with applications in computer science, from operating systems to building servers. Using binary trees can reduce the complexity of various problems to a large extent.

Height of a Binary Tree in Data Structure

The depth of a tree node is equal to the number of edges from the node to the tree's root node. A root node has a depth of 0.

The height of a tree node is equal to the number of edges on the longest path from the node to a leaf. A leaf node has a height of 0.
In this blog, we will be covering a very common question on Binary trees: How can we calculate the height of a binary tree?

Recommended: Try the Problem yourself before moving on to the solution

What is the Height of a Binary tree in Data structure?

First, let us understand the concept of the height of a binary tree. The height of a binary tree is the maximum distance from the root node to any leaf node. First, let's discuss the recursive approach to calculating the height of a binary tree.

We will start from the root node and initially, the height will be 0.
We will recursively calculate the height of the left subtree.
Similarly, we will calculate the height of the right subtree.
Now I will calculate the height of the current node by adding 1 to the max height between the right and left subtree.

Using Recursion

We can solve this problem using a recursive algorithm which will be used to traverse the binary tree. This traversal is similar to depth-first search in the graph algorithm. Let us understand this algorithm with the help of the code given below:

C++

#include<iostream>
 using namespace std; 
 
 struct Node {
     int val;
     Node *left;
     Node *right;
     Node(int x){
      val = x; Node* left = NULL; Node*right = NULL;
     }
  };
  
   
int maxDepth(Node* root) {
    	
    // this is the base case when root is null we simply return 0
    if(root == NULL)return 0; 
    // here we are computing max height that is present in the left and 
    // right subtree, We are adding one for the current node. 
    else return max( maxDepth(root->left), maxDepth(root->right) + 1 ); 
    	
}
int main()
{
    // constructing the tree
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->right = new Node(4);
    root->right->right = new Node(5);
    root->left->right->right = new Node(6);
    root->left->right->right->right = new Node(7);
    int height = maxDepth(root); 
    cout<<"The height of a binary tree is: "<<height<<endl;
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

C

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int val;
    struct Node* left;
    struct Node* right;
};

struct Node* newNode(int data) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->val = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

int maxDepth(struct Node* root) {
    if (root == NULL) return 0;
    else {
        int leftDepth = maxDepth(root->left);
        int rightDepth = maxDepth(root->right);
        return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
    }
}

int main() {
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->right = newNode(4);
    root->right->right = newNode(5);
    root->left->right->right = newNode(6);
    root->left->right->right->right = newNode(7);

    int height = maxDepth(root);
    printf("The height of the binary tree is: %d\n", height);
    return 0;
}

You can also try this code with Online C Compiler

Run Code

Java

class Node {
    int val;
    Node left, right;

    public Node(int val) {
        this.val = val;
        left = right = null;
    }
}

public class Main {
    public static int maxDepth(Node root) {
        if (root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }

    public static void main(String[] args) {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);

        System.out.println("The height of the binary tree is: " + maxDepth(root));
    }
}

You can also try this code with Online Java Compiler

Run Code

Python

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def max_depth(root):
    if root is None:
        return 0
    return max(max_depth(root.left), max_depth(root.right)) + 1

# Constructing the tree
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.right = Node(4)
root.right.right = Node(5)
root.left.right.right = Node(6)
root.left.right.right.right = Node(7)

height = max_depth(root)
print("The height of the binary tree is:", height)

You can also try this code with Online Python Compiler

Run Code

C#

using System;

class Node {
    public int val;
    public Node left, right;

    public Node(int val) {
        this.val = val;
        left = right = null;
    }
}

class Program {
    public static int MaxDepth(Node root) {
        if (root == null) return 0;
        return Math.Max(MaxDepth(root.left), MaxDepth(root.right)) + 1;
    }

    static void Main() {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);

        Console.WriteLine("The height of the binary tree is: " + MaxDepth(root));
    }
}

JavaScript

class Node {
    constructor(val) {
        this.val = val;
        this.left = this.right = null;
    }
}

function maxDepth(root) {
    if (root === null) return 0;
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}

// Constructing the tree
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.right = new Node(4);
root.right.right = new Node(5);
root.left.right.right = new Node(6);
root.left.right.right.right = new Node(7);

console.log("The height of the binary tree is:", maxDepth(root));

You can also try this code with Online Javascript Compiler

Run Code

Output :

The height of a binary tree is: 5

Time Complexity - O(N), as we are traversing every node once, the time complexity to compute the height of a binary tree is of the order N, where N is the number of nodes present in the tree.

Space Complexity -The space complexity is O(H), where H is the height of the binary tree considering the stack space used during recursion while checking for symmetric subtrees. In the worst case(skewed binary tree), H can be equal to N, where N is the number of nodes in the tree.

This problem given above can be modified as - Given the node’s address, we have to find the height of that particular node in the tree. We can simply find the given node and start traversing to the left and right. The function to compute the following is :

Using Level Order Traversal

To calculate the maximum depth of a binary tree using Level Order Traversal (Breadth-First Search) in different programming languages. This approach uses a queue to traverse each level of the tree and count the depth.

C++

#include <iostream>
#include <queue>
using namespace std;

struct Node {
    int val;
    Node *left, *right;
    Node(int x) : val(x), left(NULL), right(NULL) {}
};

int maxDepth(Node* root) {
    if (!root) return 0;

    queue<Node*> q;
    q.push(root);
    int depth = 0;

    while (!q.empty()) {
        int levelSize = q.size();
        depth++;

        for (int i = 0; i < levelSize; i++) {
            Node* node = q.front();
            q.pop();

            if (node->left) q.push(node->left);
            if (node->right) q.push(node->right);
        }
    }
    return depth;
}

int main() {
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->right = new Node(4);
    root->right->right = new Node(5);
    root->left->right->right = new Node(6);
    root->left->right->right->right = new Node(7);

    cout << "The height of the binary tree is: " << maxDepth(root) << endl;
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

C

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int val;
    struct Node* left;
    struct Node* right;
};

struct Node* newNode(int data) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->val = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

int maxDepth(struct Node* root) {
    if (!root) return 0;

    struct Node* queue[100];
    int front = 0, rear = 0, depth = 0;

    queue[rear++] = root;

    while (front < rear) {
        int levelSize = rear - front;
        depth++;

        for (int i = 0; i < levelSize; i++) {
            struct Node* node = queue[front++];
            if (node->left) queue[rear++] = node->left;
            if (node->right) queue[rear++] = node->right;
        }
    }
    return depth;
}

int main() {
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->right = newNode(4);
    root->right->right = newNode(5);
    root->left->right->right = newNode(6);
    root->left->right->right->right = newNode(7);

    printf("The height of the binary tree is: %d\n", maxDepth(root));
    return 0;
}

You can also try this code with Online C Compiler

Run Code

Java

import java.util.LinkedList;
import java.util.Queue;

class Node {
    int val;
    Node left, right;

    public Node(int val) {
        this.val = val;
        left = right = null;
    }
}

public class Main {
    public static int maxDepth(Node root) {
        if (root == null) return 0;

        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;

        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            depth++;

            for (int i = 0; i < levelSize; i++) {
                Node node = queue.poll();
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
        }
        return depth;
    }

    public static void main(String[] args) {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);

        System.out.println("The height of the binary tree is: " + maxDepth(root));
    }
}

You can also try this code with Online Java Compiler

Run Code

Python

from collections import deque

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def max_depth(root):
    if not root:
        return 0

    queue = deque([root])
    depth = 0

    while queue:
        level_size = len(queue)
        depth += 1

        for _ in range(level_size):
            node = queue.popleft()
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

    return depth

# Constructing the tree
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.right = Node(4)
root.right.right = Node(5)
root.left.right.right = Node(6)
root.left.right.right.right = Node(7)

print("The height of the binary tree is:", max_depth(root))

You can also try this code with Online Python Compiler

Run Code

C#

using System;
using System.Collections.Generic;

class Node {
    public int val;
    public Node left, right;

    public Node(int val) {
        this.val = val;
        left = right = null;
    }
}

class Program {
    public static int MaxDepth(Node root) {
        if (root == null) return 0;

        Queue<Node> queue = new Queue<Node>();
        queue.Enqueue(root);
        int depth = 0;

        while (queue.Count > 0) {
            int levelSize = queue.Count;
            depth++;

            for (int i = 0; i < levelSize; i++) {
                Node node = queue.Dequeue();
                if (node.left != null) queue.Enqueue(node.left);
                if (node.right != null) queue.Enqueue(node.right);
            }
        }
        return depth;
    }

    static void Main() {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);

        Console.WriteLine("The height of the binary tree is: " + MaxDepth(root));
    }
}

JavaScript

class Node {
    constructor(val) {
        this.val = val;
        this.left = this.right = null;
    }
}

function maxDepth(root) {
    if (root === null) return 0;

    let queue = [root];
    let depth = 0;

    while (queue.length > 0) {
        let levelSize = queue.length;
        depth++;

        for (let i = 0; i < levelSize; i++) {
            let node = queue.shift();
            if (node.left !== null) queue.push(node.left);
            if (node.right !== null) queue.push(node.right);
        }
    }
    return depth;
}

// Constructing the tree
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.right = new Node(4);
root.right.right = new Node(5);
root.left.right.right = new Node(6);
root.left.right.right.right = new Node(7);

console.log("The height of the binary tree is:", maxDepth(root));

You can also try this code with Online Javascript Compiler

Run Code

Output

The height of the binary tree is: 5

Modified Height of a binary tree

The modified height of a binary tree is calculated by counting the number of edges along the longest path from the root node to the farthest leaf node. Unlike standard height, which counts nodes, this version only counts edges, so a single-node tree has a height of 0.

C++

#include<iostream>
using namespace std;

struct Node {
    int val;
    Node *left;
    Node *right;
    Node(int x) {
        val = x;
        left = right = NULL;
    }
};

// Calculate height from the given node
int Solve(Node *root) {
    if (root == NULL) return 0;
    return 1 + max(Solve(root->left), Solve(root->right));
}

// Find node and print height from that node
void find(Node *root, int data) {
    if (root == NULL) return;
    if (root->val == data) {
        cout << "The height of the binary tree from node " << data << " is: " << Solve(root) << endl;
        return;
    }
    find(root->left, data);
    find(root->right, data);
}

int main() {
    Node *root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->right = new Node(4);
    root->right->right = new Node(5);
    root->left->right->right = new Node(6);
    root->left->right->right->right = new Node(7);
    find(root, 4);
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

C

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int val;
    struct Node *left;
    struct Node *right;
};

struct Node* createNode(int x) {
    struct Node *node = (struct Node*)malloc(sizeof(struct Node));
    node->val = x;
    node->left = node->right = NULL;
    return node;
}

int Solve(struct Node *root) {
    if (root == NULL) return 0;
    int leftHeight = Solve(root->left);
    int rightHeight = Solve(root->right);
    return 1 + (leftHeight > rightHeight ? leftHeight : rightHeight);
}

void find(struct Node *root, int data) {
    if (root == NULL) return;
    if (root->val == data) {
        printf("The height of the binary tree from node %d is: %d\n", data, Solve(root));
        return;
    }
    find(root->left, data);
    find(root->right, data);
}

int main() {
    struct Node *root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->right = createNode(4);
    root->right->right = createNode(5);
    root->left->right->right = createNode(6);
    root->left->right->right->right = createNode(7);
    find(root, 4);
    return 0;
}

You can also try this code with Online C Compiler

Run Code

Java

class Node {
    int val;
    Node left, right;

    Node(int x) {
        val = x;
        left = right = null;
    }
}

public class BinaryTreeHeight {

    public static int solve(Node root) {
        if (root == null) return 0;
        return 1 + Math.max(solve(root.left), solve(root.right));
    }

    public static void find(Node root, int data) {
        if (root == null) return;
        if (root.val == data) {
            System.out.println("The height of the binary tree from node " + data + " is: " + solve(root));
            return;
        }
        find(root.left, data);
        find(root.right, data);
    }

    public static void main(String[] args) {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);
        find(root, 4);
    }
}

You can also try this code with Online Java Compiler

Run Code

Python

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def solve(root):
    if root is None:
        return 0
    return 1 + max(solve(root.left), solve(root.right))

def find(root, data):
    if root is None:
        return
    if root.val == data:
        print(f"The height of the binary tree from node {data} is: {solve(root)}")
        return
    find(root.left, data)
    find(root.right, data)

# Construct the binary tree
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.right = Node(4)
root.right.right = Node(5)
root.left.right.right = Node(6)
root.left.right.right.right = Node(7)
find(root, 4)

You can also try this code with Online Python Compiler

Run Code

C#

using System;

class Node {
    public int val;
    public Node left, right;

    public Node(int x) {
        val = x;
        left = right = null;
    }
}

class BinaryTreeHeight {

    public static int Solve(Node root) {
        if (root == null) return 0;
        return 1 + Math.Max(Solve(root.left), Solve(root.right));
    }

    public static void Find(Node root, int data) {
        if (root == null) return;
        if (root.val == data) {
            Console.WriteLine($"The height of the binary tree from node {data} is: {Solve(root)}");
            return;
        }
        Find(root.left, data);
        Find(root.right, data);
    }

    public static void Main() {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);
        Find(root, 4);
    }
}

JavaScript

class Node {
    constructor(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

function solve(root) {
    if (root === null) return 0;
    return 1 + Math.max(solve(root.left), solve(root.right));
}

function find(root, data) {
    if (root === null) return;
    if (root.val === data) {
        console.log(`The height of the binary tree from node ${data} is: ${solve(root)}`);
        return;
    }
    find(root.left, data);
    find(root.right, data);
}

// Construct the binary tree
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.right = new Node(4);
root.right.right = new Node(5);
root.left.right.right = new Node(6);
root.left.right.right.right = new Node(7);
find(root, 4);

You can also try this code with Online Javascript Compiler

Run Code

Output :

The height of a binary tree is: 3

Time Complexity - O(N), as we are traversing every node once, the time complexity to compute the height of a binary tree is N, where N is the number of nodes present in the tree.

Space Complexity - The space complexity is O(H), where H is the height of the binary tree considering the stack space used during recursion while checking for symmetric subtrees. In the worst case(skewed binary tree), H can be equal to N, where N is the number of nodes in the tree.

Check out this problem - Mirror A Binary Tree

Depth of a node in a binary tree

Now let us calculate the depth of a node in a binary tree -
We can simply calculate the depth of the tree by subtracting the height of the given node by the height of the root node. i.e -

Height(root) - Height(given node)

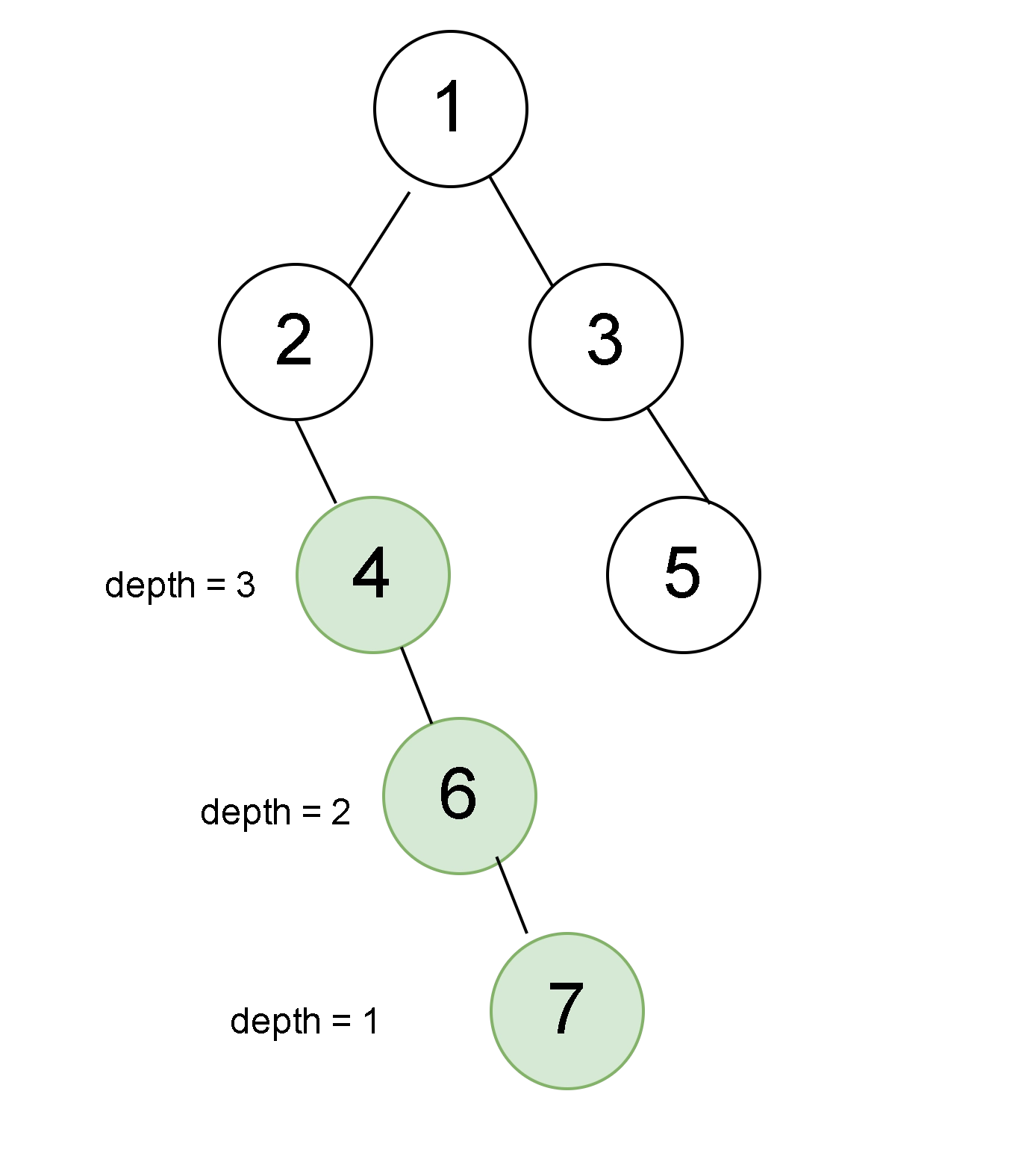
We can also calculate the depth of the binary tree by applying the recursive algorithm. We initiate the depth to be 0 initially when we are present at the root node. On every recursive call we add one to the depth and return when the given element for which depth has to be calculated is equal to the current element.

C++

 
#include<iostream>
 using namespace std; 
 
 struct Node {
     int data;
     Node *left;
     Node *right;
     Node(int x){
      data = x; Node* left = NULL; Node*right = NULL;
     }
  };
  
   
int maxDepth(Node * root, int val, int depth)
{
  // Root being null means tree doesn't exist.
  if (root == NULL)
    return 0;
  if(root->data == val)return depth; 
  
  // Get the depth of the left and right subtree 
  // using recursion.
  int leftDepth = maxDepth(root->left, val, depth + 1);
  int rightDepth = maxDepth(root->right, val, depth + 1);


 // if any of the subtree does not contain the element then it will return
 // null and we will simply return the value from the other tree. 
 return max(leftDepth, rightDepth); 
 
}


int main()
{
   // constructing the tree
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->right = new Node(4);
    root->right->right = new Node(5);
    root->left->right->right = new Node(6);
    root->left->right->right->right = new Node(7);
    int val = 4; 
    int depth = maxDepth(root, val, 1); 
    cout<<"The depth of a binary tree node " <<val << " is: "<<depth<<endl;
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

C

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int data;
    struct Node *left;
    struct Node *right;
};

struct Node* createNode(int x) {
    struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = x;
    newNode->left = newNode->right = NULL;
    return newNode;
}

int maxDepth(struct Node *root, int val, int depth) {
    if (root == NULL) return 0;
    if (root->data == val) return depth;
    
    int leftDepth = maxDepth(root->left, val, depth + 1);
    int rightDepth = maxDepth(root->right, val, depth + 1);

    return (leftDepth > rightDepth) ? leftDepth : rightDepth;
}

int main() {
    struct Node* root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->right = createNode(4);
    root->right->right = createNode(5);
    root->left->right->right = createNode(6);
    root->left->right->right->right = createNode(7);
    
    int val = 4;
    int depth = maxDepth(root, val, 1);
    printf("The depth of binary tree node %d is: %d\n", val, depth);
    return 0;
}

You can also try this code with Online C Compiler

Run Code

Java

class Node {
    int data;
    Node left, right;

    Node(int x) {
        data = x;
        left = right = null;
    }
}

public class BinaryTreeDepth {
    public static int maxDepth(Node root, int val, int depth) {
        if (root == null) return 0;
        if (root.data == val) return depth;
        
        int leftDepth = maxDepth(root.left, val, depth + 1);
        int rightDepth = maxDepth(root.right, val, depth + 1);

        return Math.max(leftDepth, rightDepth);
    }

    public static void main(String[] args) {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);
        
        int val = 4;
        int depth = maxDepth(root, val, 1);
        System.out.println("The depth of binary tree node " + val + " is: " + depth);
    }
}

You can also try this code with Online Java Compiler

Run Code

Python

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

def maxDepth(root, val, depth):
    if root is None:
        return 0
    if root.data == val:
        return depth
    
    leftDepth = maxDepth(root.left, val, depth + 1)
    rightDepth = maxDepth(root.right, val, depth + 1)
    
    return max(leftDepth, rightDepth)

# Construct the binary tree
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.right = Node(4)
root.right.right = Node(5)
root.left.right.right = Node(6)
root.left.right.right.right = Node(7)

val = 4
depth = maxDepth(root, val, 1)
print(f"The depth of binary tree node {val} is: {depth}")

You can also try this code with Online Python Compiler

Run Code

C#

using System;

class Node {
    public int data;
    public Node left, right;

    public Node(int x) {
        data = x;
        left = right = null;
    }
}

class BinaryTreeDepth {
    public static int MaxDepth(Node root, int val, int depth) {
        if (root == null) return 0;
        if (root.data == val) return depth;
        
        int leftDepth = MaxDepth(root.left, val, depth + 1);
        int rightDepth = MaxDepth(root.right, val, depth + 1);

        return Math.Max(leftDepth, rightDepth);
    }

    public static void Main() {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.right = new Node(4);
        root.right.right = new Node(5);
        root.left.right.right = new Node(6);
        root.left.right.right.right = new Node(7);
        
        int val = 4;
        int depth = MaxDepth(root, val, 1);
        Console.WriteLine($"The depth of binary tree node {val} is: {depth}");
    }
}

JavaScript

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

function maxDepth(root, val, depth) {
    if (root === null) return 0;
    if (root.data === val) return depth;

    const leftDepth = maxDepth(root.left, val, depth + 1);
    const rightDepth = maxDepth(root.right, val, depth + 1);

    return Math.max(leftDepth, rightDepth);
}

// Construct the binary tree
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.right = new Node(4);
root.right.right = new Node(5);
root.left.right.right = new Node(6);
root.left.right.right.right = new Node(7);

const val = 4;
const depth = maxDepth(root, val, 1);
console.log(`The depth of binary tree node ${val} is: ${depth}`);

You can also try this code with Online Javascript Compiler

Run Code

Output :

The depth of a binary tree is: 3

Time Complexity - O(N), as we are traversing every node once, the time complexity to compute the height of a binary tree is N, where N is the number of nodes present in the tree. In the worst case, our node will be a leaf node and we will end up traversing all the nodes.

Frequently Asked Questions

What is a complete binary tree of height?

A complete binary tree of height h is a binary tree where all levels are fully filled, except possibly the last level, which is filled from left to right. It maximizes the number of nodes for a given height.

What is the height of an empty binary tree?

The height of an empty binary tree is typically defined as -1. Since there are no nodes, it has no levels, and therefore a height of -1 represents its non-existence.

How does the height of a binary tree relate to its number of nodes?

In a binary tree, height affects the number of nodes, where a tree with height h can have between h + 1 and 2^(h+1) - 1 nodes, depending on how fully the tree is filled.

How does balancing affect the height of a binary tree?

Balancing minimizes the height of a binary tree by distributing nodes evenly across levels. This optimizes search, insertion, and deletion operations by keeping height close to the minimum possible for the number of nodes.

Can a binary tree have a negative height?

Yes, a binary tree can have a height of -1, which typically denotes an empty tree. This convention indicates that the tree has no nodes or levels.

Conclusion

In this article, we explored how to find the height or depth of a binary tree. This is a straightforward recursive problem that can be solved with a simple application of recursion. Understanding this concept is essential, as it has applications in various binary tree-related problems. For more in-depth learning, you can also refer to our course.