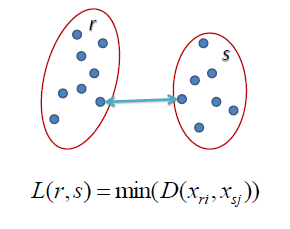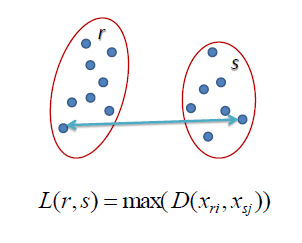Hierarchical Clustering

Ways to build Hierarchical clustering :

There are two ways to achieve Hierarchical clustering:

1) Top-Down

2) Bottom-Up

1) Top-Down approach:
This is also called the Divisive approach. It says that, If we have n data points, let's make the entire data points as one cluster called as root and then break it into two groups, say S1 and S2.

There are 2n number of ways for selecting two subsets S1 and S2, out of n data points. For each subset S1 and S2, we try to find the distance between these clusters and pick up that cluster having a maximum distance 

Maximum distance = max{ d(x,y), where xS1 and yS2}

In this way we can achieve a perfect Hierarchical clustering tree. But it requires a lot of work( exponential work). We can try getting a very good tree that gives a decent accuracy level despite getting the perfect tree. So, we will split n data points into two clusters by other algorithms, say k means, and recursively call on each group to further break down into more sets. 

2) Bottom-Up approach
This is also called Agglomerative clustering. It says that for n data points, let's make each data point a cluster and then merge two of these clusters closest to each other into one and recursively merge other clusters. The Hierarchical clustering Technique can be visualized using a Dendrogram. 

A Dendrogram is a tree-like structure that records the sequence of merges or splits.

Minimum distance = min{ d(x,y), where xS1 and yS2}

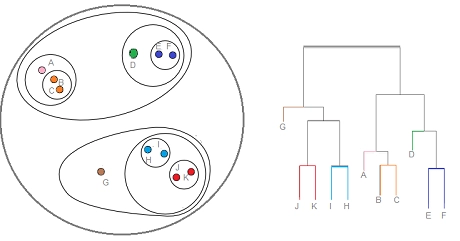
                       Source: statisticshowto.com

Similarities between two clusters

There are various approaches to calculate the similarity between two clusters:

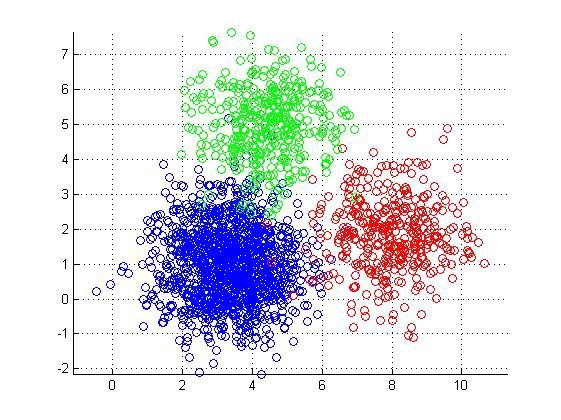
MIN

MIN is also known as the single-linkage algorithm, which defines the similarity of two clusters r and s as the minimum of the similarity  between points xi and xj such that xi r and xj s..

i.e,  min{ d(p1,p2), where p1S1 and p2S2}

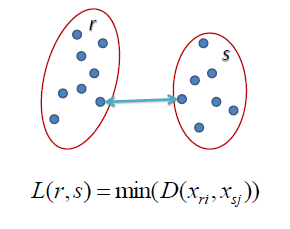
This approach can separate two clusters as long as the gap between them is not small but can’t distinguish properly when the data points are overlapping.

MAX: 

MAX is called a complete linkage algorithm which defines the similarity of two clusters r and s as the maximum of the similarity between points xi and xj such that xi r and xj s..

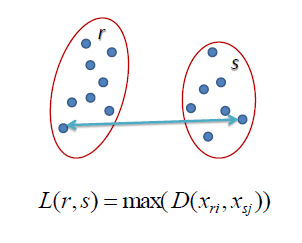
If the data points are overlapping, the MAX approach does well, but this approach tends to break large clusters.

Group Average:

The algorithm takes all the pairs of points and calculates their average of similarities. Group average distance between clusters Ci and Cj is the average distance between any point in Ci and any point in Cj is given by:

The group average does well if there is noise between clusters. 

Space and Time Complexities of Hierarchical Clustering:

A lot of space is required to store the Hierarchy Tree, So the Space complexity is in the order of the square of n, i.e., O(n2).

The Time complexity is if the order of cube of n, i.e., O(n3).

Pros and Cons of Hierarchical clustering:

Pros:

• Dendrogram are great for visualization
• Provides Hierarchical relation between clusters
• The model itself can obtain the optimal number of clusters.

Cons:

• As the time and space complexities are very high, it is not suitable for large datasets.
• It is not easy to define the level of clusters.

FAQs:

1. Each point in a Hierarchical clustering is a part of:
   -> Many Clusters
    
2. Basic idea behind Hierarchical clustering is:
   -> To make clusters within clusters.
    
3. Which of the following statements are valid for the top-down approach?
   i) All the observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.
   ii) Also known as the Divisive approach
    
4. Which of the following statements are true for the bottom-up approach?
   i)Each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
   ii)Also known as the Algomerrative approach
    
5. What is a Dendrogram?
   -> A Dendrogram is a tree-like structure that records the sequence of merges or splits.

Key Takeaways:

This comes to the end of the discussion on Hierarchical clustering. There are various clustering algorithms in Unsupervised Learning that help in predicting the output without the labels.

For the implementation part, Must visit: How to Perform Hierarchical Clustering in Python( Step by Step) 

Happy Learning✌✌