Introduction
Suppose we are given an array of strings, and we are asked if we can chain the strings to form a circle which means that the last element of any string has to be the same as the first element of the next string.
Let’s understand the problem with an example-
Suppose we have an array of strings given below- {“aabc”, “cert”, “ter”, “reha”}
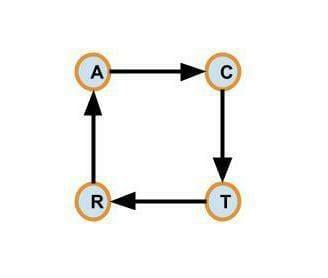
In the above example, we can see that the last letter is similar to the first letter of the next string for each string. So we can form a circle from these strings.
Whereas if we take another example, {"ufiw", "jufe", "eifd", "doer"}
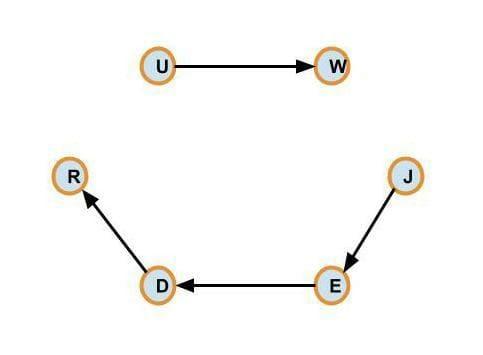
We will see that the last element of the first string is not similar to the first element of the second string, and also, the last element of the last string is not similar to the first element of the first string. Thus we can not form a circle using them.
And if we look at another example, {“ehfc”, “jte”, “dpoij”, “ilasd”, “cji”}
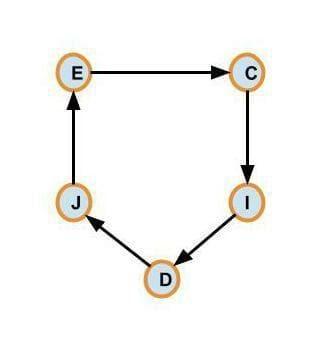
The strings in the above example can be rearranged in the following order {"ehfc", "cji", "ilasd", "dpoij", "jte"}.
Then this array of strings can form a circle.
Now we need to devise a method to check if any given array of strings can form a circle or not. For this problem, We will be using a method based on eulerian circuits in directed graphs.
So, let's first understand what your eulerian circuits are-
The eulerian circuit is a path in a graph that visits every node exactly once. It has the same vertex as its starting and ending point. Any graph that contains an eulerian circuit is known as an eulerian graph.
We can check if a graph is an eulerian graph or not, with the help of the following conditions-
- Every vertex has the same value of indegree and outdegree
- All vertices with non zero degrees have to belong to a single strongly connected component
So we start with a graph having all 26 characters of the alphabet as nodes, then we form a directed graph by connecting each string's first and last character. Then we check if that graph is an eulerian graph or not. If the graph is eulerian, then the array of strings can form a circle, and if the graph is not an eulerian graph, the strings can not form a circle.
Algorithm for the solution
- Create a graph with all 26 alphabets as nodes.
- For each string, add an edge from the first character to the last character of the string.
- Check if the formed graph is eulerian or not.
- If it's eulerian return that the array of strings can form a circle, else return that they can not form a circle.




