Introduction
This blog will discuss how to count the total number of nodes in a complete binary tree If we are given its root. For example, consider the tree shown below. If we count the total number of nodes in it, the answer will be 12.
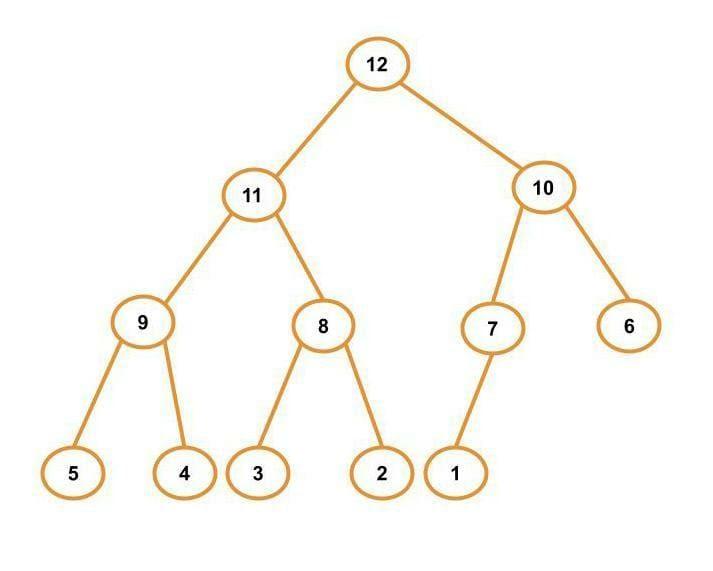
There could be many ways to count the number of nodes in a complete binary tree, but we will learn only a few of them. But before moving straight to the solution, let's refresh our knowledge of binary and complete binary trees.
A binary tree is a tree in which all the nodes can have at most two children, and a complete binary tree is a tree in which all the levels must be filled except the last level, which is filled from left to right direction.
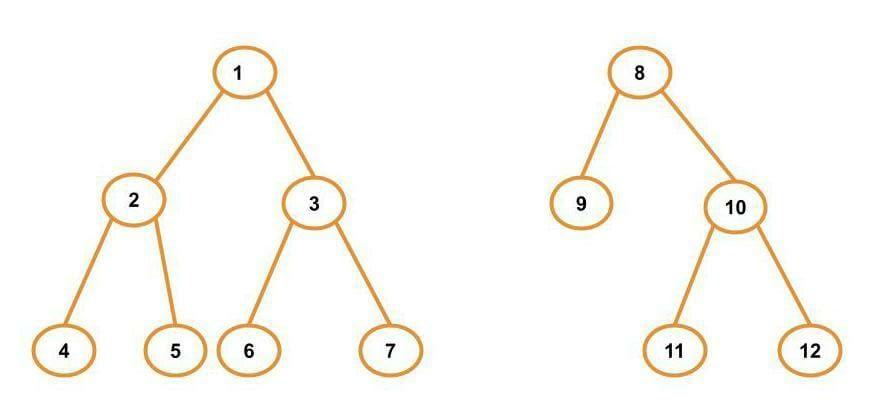
For example, in the figure below, the tree on the left is a complete binary tree. But, the tree on the right is not a complete binary tree.
The basic solution to this problem is to traverse through the tree and count the number of nodes. And, the efficient approach uses the relation between height and the number of nodes in the complete binary tree. So let's begin with the basic approach -
Also, see the implementation of the Binary tree in C and Data Structures for a better understanding.
Naive Approach
The basic approach to this problem is quite simple. We perform the DFS traversal of the binary tree and keep a count of the notes we encounter during the traversal.
Algorithm
- Construct a complete binary tree or take it from user input.
- Create a function to count the number of nodes in the tree. It takes the root of the tree as an argument and returns the number of nodes.
- If the root is null in the count function, return 0; otherwise, return the sum of the number of nodes in the left, right subtree, and one.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
//Class for the nodes of a tree.
class treenode {
public:
int value;
treenode* left;
treenode* right;
treenode(int num)
{
value = num;
left = nullptr;
right = nullptr;
}
};
//Function to count nodes in a complete binary tree.
int count(treenode* root)
{
//Base case.
if (!root)
{
return 0;
}
return 1 + count(root->left) + count(root->right);
}
//Driver function.
int main()
{
treenode* root = new treenode(12);
root->left = new treenode(11);
root->right = new treenode(10);
root->left->left = new treenode(9);
root->left->right = new treenode(8);
root->right->left = new treenode(7);
root->right->right = new treenode(6);
root->left->left->left = new treenode(5);
root->left->left->right = new treenode(4);
root->left->right->left = new treenode(3);
root->left->right->right = new treenode(2);
root->right->left->left = new treenode(1);
cout<<"The total number of nodes in this complete binary tree is- " <<count(root)<<endl;
return 0;
}
Output-
The total number of nodes in this complete binary tree is- 12Complexity Analysis
Time complexity - O(N).
Space complexity - O(1).





