Introduction
In this blog, we will be discussing the level-order traversal-based method to print a binary tree in vertical order. We already have discussed a few methods like the basic horizontal distance-based method, hashmap, and preorder traversal-based methods to print a binary tree in vertical order in the previous blogs. Check them out to understand these basic methods before diving into the advanced method discussed in this blog.
Let's begin the blog again with a brief introduction of the problem-Suppose we have with the following binary tree, and we are asked to print it in vertical order.
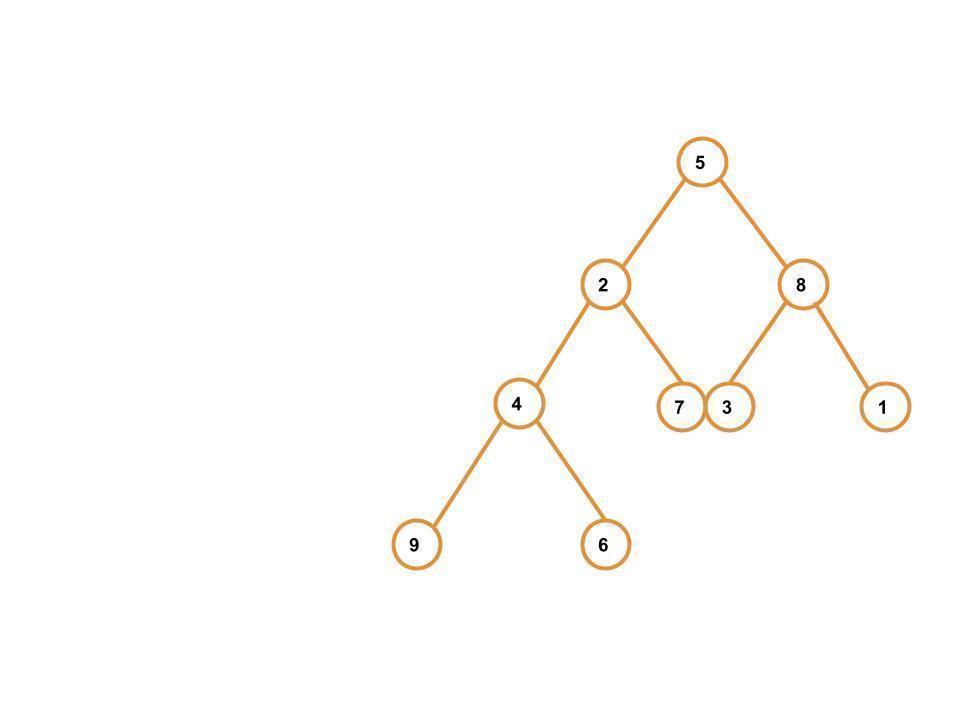
we will get the following output on printing the above binary tree in the vertical order -
| 9 4 2 6 5 7 3 8 11 |
We can observe from the output that we need to start by printing the leftmost node in the tree, then the next leftmost node, and so on. And if two or more nodes are equally distant from the root, we print them in top-to-bottom order. Since we have understood the problem, let’s move on to the level order traversal-based solution-
The level-order traversal-based approach
This approach to printing a binary tree in vertical order uses a hashmap for each branch of the binary tree. Then it pushes the nodes into a queue while leveling the order traversal of the binary tree. Then we pop the front of the queue and push its values in the map. Finally, we traverse through the map and print the array of nodes stored in it as values.
Algorithm for the map-based approach
- Create a binary tree or take it as input from the user.
- Create a map to store horizontal distance and an array of nodes associated with that values of horizontal distance as key-value pairs.
- We then create a queue for holding the nodes during the level order traversal of the tree.
- We start with pushing the root into the queue with its horizontal distance as 0.
- Then we pop the front of the queue and push its values on the map.
- Then we make recursive calls for the left and right branches to perform the above steps.
In the level order traversal of a binary tree, while moving onto the left branch of the tree, the value of horizontal distance decreases by 1 unit, and if we move towards the right branch, the value of horizontal distance increases by 1 unit. - Finally, we Traverse the map to print all the arrays of nodes stored in the map.
Implementation of the map-based approach
#include <bits/stdc++.h>
using namespace std;
struct node
{
int data;
struct node *left, *right;
};
//To create a new node for the binary tree.
node *createnode(int data)
{
node *var = new node;
var->data = data;
var->left = var->right = NULL;
return var;
}
//Function to create the map and do the level order
//traversal of the tree to find vertical order of the
//nodes and then printing the values in the map.
void printtreevert(node* root)
{
//Base case.
if (root==nullptr)
{
return;
}
//Creat a map to store the node and its
//distance in pair.
map<int,vector<int> > mp;
int hordist=0;
//Creating a queue for level order traversal of the
//binary tree by holding the node and its horizontal
//distance in pair.
queue<pair<node*, int> >q;
q.push(make_pair(root, hordist));
while(q.empty()!=true)
{
//Extracting the value from the top of the queue.
pair<node*, int>var=q.front();
q.pop();
hordist=var.second;
node* newnode=var.first;
//pushing the value popped from hashtable into
//the map.
mp[hordist].push_back(newnode->data);
//Making recursive calls for the left and right
//branches of the node.
if(newnode->left!=nullptr)
{
q.push(make_pair(newnode->left, hordist-1));
}
if(newnode->right!=nullptr)
{
q.push(make_pair(newnode->right, hordist+1));
}
}
//To print the arrays of the nodes stored in the map.
map<int, vector<int> >::iterator itr;
for(itr=mp.begin();itr!=mp.end();itr++)
{
for(int i=0;i<itr->second.size();i++)
{
cout<<itr->second[i]<<" ";
}
cout << endl;
}
}
//Driver function.
int main()
{
//Creating the binary tree.
node *root=createnode(5);
root->left=createnode(2);
root->right=createnode(8);
root->left->left=createnode(4);
root->left->right=createnode(7);
root->right->left=createnode(3);
root->right->right=createnode(11);
root->left->left->left=createnode(9);
root->left->left->right=createnode(6);
printtreevert(root);
return 0;
}
Output
| 9 4 2 6 5 7 3 8 11 |
The time complexity of the above approach is O(N*log(N)), where N is the number of nodes in it, as the map in STL takes O(log(N)) time for all the operations, and we processed all the N nodes.
The space complexity of the above approach is O(N).
Check out this problem - Diameter Of Binary Tree




