Solution Approach
The approach is to make a graph of all the contacts as nodes and connect the nodes(i.e., contacts), which have the same value for any data field. Once we are done creating a graph of contacts now, we will have some contacts(i.e., Contacts having the same value for any data field) as connected components of the Graph.
Now the problem reduces to calculating the number of connected components in a graph for which we can use any traversal method, DFS Algorithm or BFS.In this article, we will implement it using BFS and see how it works.
Steps of the Algorithm
-
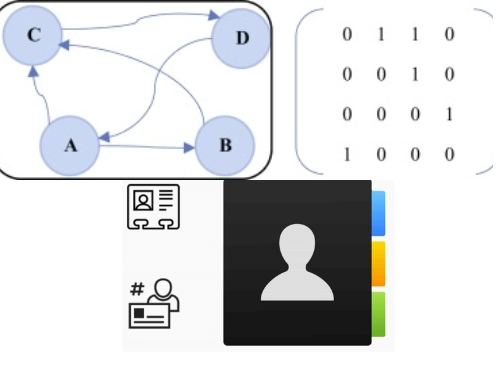
The first step is to build the graph. We are using the adjacency matrix to represent the graph for our problem. An adjacency matrix is an n*n matrix where the entry (i,j) is 1 if there is an edge connecting i and j; otherwise 0.
-
To build the adjacency matrix, we check if any of the three fields of i is the same as any of the three fields of j. If any such case is encountered, mark adj[i][j] as 1.
-
Next, we need to find the connected components of the created graph. For this purpose, we are using BFS.
-
The connected nodes are visited in a single run of BFS, so for each run for BFS, we print the connected nodes in the same line separated by whitespace.
-
After the BFS ends, we provide a new line, and we check for the remaining nodes of the graph. We have used an array visited to keep track of the nodes that are already visited.
In this manner, all the connected components of the graph are of the same contact and are printed accordingly.
Let us understand the steps of the algorithm by performing a dry run on the given example.
Example input
listOfContacts = [["Aastha", "aastha@gmail.com", "+6725872"],
["Anshit", "anshit@gmail.com", "+5412312"],
["rahul19", "+5412312", "rahul@cn.com"],
["+2231210", "rani@cn.com", "Rani"],
["Bhallaldev", "+8784312", "rani@cn.com"],
["+5412302", "rahul19", "rahull10@linkedin.com"]]
In the first step, we create an adjacency list for the given data. We see that contact 0 has no common detail with other contacts. Contact 1 and contact 2 have the same contact number. Contact 2 and contact 5 have the same username. Contact 3 and 4 have the same email address. This results in the formation of the below adjacency matrix.
[ [ 1, 0, 0, 0, 0, 0],
[ 0, 1, 1, 0, 0, 0],
[ 0, 1, 1, 0, 0, 1],
[ 0, 0, 0, 1, 1, 0],
[ 0, 0, 0, 1, 1, 0],
[ 0, 0, 1, 0, 0, 1] ]
Now the next step is to find the connected components; we begin with index 0. 0 has no other connected node. So, it is a single disconnected component. We print 0.
Next, for index 1. We have adj[1][2] = 1. So, we enqueue 2, and since no other node has an edge with 1, we dequeue 1. Now we check for 2. We find an edge with a new node with index 5. So, we add 5 to the queue. We check for 5 and find no new node. Hence, we print 1 2 5.
Next, we do not run BFS for index 2 since it is already visited.
For index 3, we check and find an edge with index 4. We print 3 4.
4 and 5 are already visited, so no need to consider them again. Hence, we get the below output as the final output.
Output
0
1 2 5
3 4
Python Implementation
'''Function to build and return the adjacency list for the graph'''
def buildGraph(listOfContacts):
n = len(listOfContacts)
'''Adjacency matrix'''
adj = [[0] * n for i in range(n)]
''' For each contact '''
for i in range(n):
curr = listOfContacts[i]
'''Compare with each other contact'''
for j in range(n):
temp = listOfContacts[j]
''' if any of the three fields of curr is similar to any of the three fields of temp, the contact is same'''
if curr[0] == temp[0] or curr[0] == temp[1] or curr[0] == temp[2] or curr[1] == temp[0] or curr[1] == temp[1] or curr[1] == temp[2] or curr[2] == temp[0] or curr[2] == temp[1] or curr[2] == temp[2] :
adj[i][j] = 1
adj[j][i] = 1
return adj
'''Function to find the same contacts from the list of contacts. '''
def sameContact(listOfContacts):
n = len(listOfContacts)
adj = buildGraph(listOfContacts)
''' q is a queue to help running BFS '''
q = []
visited = [0] * n
'''Performing BFS'''
for i in range(n):
if not visited[i]:
print(i, end = ' ')
q.append(i)
visited[i] = 1
'''Run until the queue is not empty'''
while(len(q) != 0):
curr = q[0]
'''check for edge with previously unvisited node'''
for j in range(n):
if adj[curr][j] and j != curr and not visited[j]:
print(j, end = ' ')
q.append(j)
visited[j] = 1
'''Enqueue from the queue'''
q.pop(0)
'''Provide a new line'''
print()
return
'''Driver Function '''
def main():
listOfContacts = [["Aastha", "aastha@gmail.com", "+6725872"],
["Anshit", "anshit@gmail.com", "+5412312"],
["rahul19", "+5412312", "rahul@cn.com"],
["+2231210", "rani@cn.com", "Rani"],
["Bhallaldev", "+8784312", "rani@cn.com"],
["+5412302", "rahul19", "rahull10@linkedin.com"]]
sameContact(listOfContacts)
'''Executing Main'''
main()

You can also try this code with Online Python Compiler
C++ Implementation
#include <iostream>
using namespace std;
#include<vector>
/* Function to build and return the adjacency list for the graph */
vector<vector<int>> buildGraph(vector<vector<string>> listOfContacts){
int n = listOfContacts.size();
vector<string> curr, temp;
/*Adjacency matrix*/
vector<vector<int>> adj(n , vector<int> (n, 0));
/*For each contact*/
for(int i =0; i<n; i++){
curr = listOfContacts[i];
/*Compare with each other contact */
for(int j =0; j<n; j++){
temp = listOfContacts[j];
/*if any of the three fields of curr is similar to any of the three fields of temp, the contact is same*/
if(curr[0] == temp[0] || curr[0] == temp[1] || curr[0] == temp[2] || curr[1] == temp[0] ||curr[1] == temp[1] || curr[1] == temp[2] || curr[2] == temp[0] || curr[2] == temp[1] || curr[2] == temp[2]){
adj[i][j] = 1;
adj[j][i] = 1;
}
}
}
return adj;
}
/*Function to find the same contacts from the list of contacts. */
void sameContact(vector<vector<string>> listOfContacts){
int n = listOfContacts.size();
vector<vector<int>> adj = buildGraph(listOfContacts);
int curr;
/* q is a queue to help running BFS */
vector<int> q;
vector<int> visited(n, 0);
/*Performing BFS*/
for(int i=0; i<n; i++){
if(!visited[i]){
cout<<i<<" ";
q.push_back(i);
visited[i] = 1;
/*Run until the queue is not empty*/
while(q.size() != 0){
curr = q[0];
/*check for edge with previously unvisited node*/
for(int j =0; j<n; j++){
if (adj[curr][j] && j != curr && (!visited[j])){
cout<<j<<" ";
q.push_back(j);
visited[j] = 1;
}
}
/*Enqueue from the queue*/
q.erase(q.begin());
}
/*Provide a new line*/
cout<<endl;
}
}
}
int main()
{
vector<vector<string>> listOfContacts;
listOfContacts = {{"Aastha", "aastha@gmail.com", "+6725872"},
{"Anshit", "anshit@gmail.com", "+5412312"},
{"rahul19", "+5412312", "rahul@cn.com"},
{"+2231210", "rani@cn.com", "Rani"},
{"Bhallaldev", "+8784312", "rani@cn.com"},
{"+5412302", "rahul19", "rahull10@linkedin.com"}};
sameContact(listOfContacts);
return 0;
}

You can also try this code with Online C++ Compiler
Output
0
1 2 5
3 4
Complexity Analysis
Time Complexity
O(n^2), where n is the number of contacts.
Reason: We used two nested loops to make a graph and traverse it, hence the time complexity of O(n^2).
Auxiliary SpaceComplexity
O(n^2), where n is the number of contacts.
Reason: We used a 2-D array(Adjacency matrix) to represent the graph hence an extra space of O(n^2) is required.
Frequently Asked Questions
What is meant by an undirected graph?
An undirected graph is a collection of connected objects (also known as vertices or nodes) where all edges are two-way.
How do you find the number of connected components on a graph?
Mark each vertex as unvisited to start. Repeat after each vertex. DFS should be used on any unvisited vertex to increase the count by one. The value of count will represent the number of connected elements in the graph following iteration over all vertices.
How does DFS work?
When a search runs into a dead end during any iteration, the Depth First Search (DFS) algorithm employs a stack to keep track of where to go next to continue the search.
How does BFS work?
BFS stands for Breadth-first search. It is a traversal algorithm for graphs where the traversal is done level by level. We traverse the nodes which are at the k level before moving to those nodes at the k+1 level.
What is a graph?
A graph is a non-linear data structure used to represent highly correlated data. It consists of vertices and edges. The vertices represent the nodes or elements of the graph, and the edges represent the relationships or connections between the nodes.
Conclusion
This article discussed the problem of identifying the same contacts from a list of contacts. We have discussed the solution approach with the implementation and complexity analysis.
We hope this blog helped you understand this problem and enhanced your knowledge about Depth-First Search and Breadth-First-Search used in Graphs.
You can also refer to our Youtube videos for more understanding of the topic:
If you find our blogs informative and interesting, please vote for them.
Happy Coding and Learning!