Approach and Explanation
The solution code given in this article is in C++. As asked in the problem statement, we use templates class in our code. The name of our templates class is DQ.
-
Our class DQ contains five private variables, which are:
- int frontIdx: stores the front index of the deque.
- int rearIdx: stores the rear index of the deque.
- DQ *dq: circular array to implement our dynamic deque.
- int dqSize: stores the size of our deque.
-
int dqCap: stores the capacity of our deque, initialize to 4.
-
Inside the constructor, we initialize the variables of our class as follows:
- We declare a new array of type DQ and size dqSize.
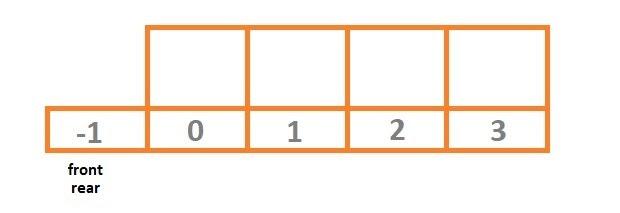
- We initialize the frontIdx and rearIdx to -1.
-
We initialize the dqSize to 0.
-
Now we create all the functions asked in the problem statement, one by one.
-
int DeQue<DQ>:: dqCapacity(): returns the value of dqCap.
-
int DeQue<DQ>:: dqRetSize(): return the value of dqSize.
-
bool DeQue<DQ>:: dqIsEmpty(): if the front and rear index are -1 returns true, else false.
-
bool DeQue<DQ>:: dqIsFull(): if the value of dqCap and dqSize is equal returns true, else false.
-
DQ DeQue<DQ>:: dqFront(): if the deque is empty, the function displays “DeQue Underflow”. Else returns the element at dq[frontIdx].
-
DQ DeQue<DQ>:: dqRear(): if the deque is empty, the function displays “DeQue Underflow”. Else returns the element at dq[rearIdx].
-
void DeQue<DQ>:: dqPushFront(DQ dQue): It does the following three tasks:
- Checks if our deque dq is full or not. If the deque is full, we double its size by multiplying dqCap by two. Create a temporary array of type DQ and copy the elements of the old array into the new. Finally, deallocate the old array.
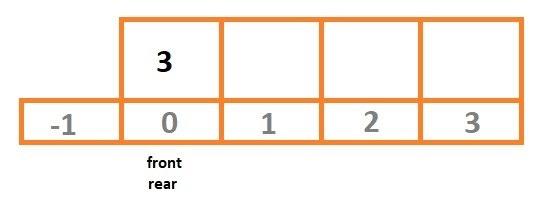
- If our deque DQ is empty, then set the front and rear index to 0, and push the element at dq[rearIdx].
-
Else set the value of frontIdx to (frontIdx+1)%dqCap push the element at dq[rearIdx], increase the value of dqSize by one.
-
void DeQue<DQ>:: dqPushRear(DQ dQue): It does the following three tasks:
- Checks if our deque dq is full or not. If the deque is full, we double its size by multiplying dqCap by two. Create a temporary array of type DQ and copy the elements of the old array into the new. Finally, deallocate the old array.
- If our deque DQ is empty, then set the front and rear index to 0, and push the element at dq[rearIdx].
-
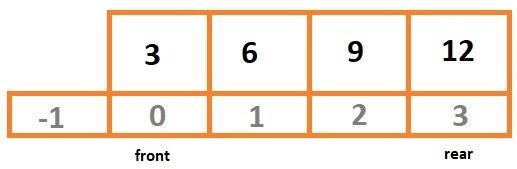
Else set the value of rearIdx to (rearIdx+1)%dqCap, push the element at dq[rearIdx], increase the value of dqSize by one.
-
int DeQue<DQ>:: dqPopFront(): This function does the following three tasks:
- If our deque is empty, display “DeQue Underflow” and exit the function.
- If our deque has only one element, then store that element in a temporary variable, set the values of frontIdx and rearIdx to -1, decrease the value of dqSize by one, and return temp.
-
Else store the element at dq[frontIdx], change the value of frontIdx to (frontIdx-1+dqCap)%dqCap, decrease the value of dqSize by one and return the stored element.
-
int DeQue<DQ>:: dqPopRear(): This function does the following three tasks:
- If our deque is empty, display “DeQue Underflow” and exit the function.
- If our deque has only one element, then store that element in a temporary variable, set the values of frontIdx and rearIdx to -1, decrease the value of dqSize by one, and return temp.
- Else store the element at dq[rearIdx], change the value of rearIdx to (rearIdx-1+dqCap)%dqCap, decrease the value of dqSize by one and return the stored element.
C++ implementation
#include<iostream>
#include<stdlib.h>
using namespace std;
template <class DQ>
class DeQue{
private:
int frontIdx;
int rearIdx;
DQ *dq;
int dqSize;
int dqCap = 4;
public:
DeQue(){
dq = new DQ[dqCap];
frontIdx = rearIdx = -1;
dqSize = 0;
}
int dqCapacity();
int dqRetSize();
bool dqIsEmpty();
bool dqIsFull();
void dqPushFront(DQ dQue);
void dqPushRear(DQ dQue);
int dqPopFront();
int dqPopRear();
DQ dqFront();
DQ dqRear();
};
template <class DQ>
int DeQue<DQ>::dqCapacity(){
return dqCap;
}
template <class DQ>
int DeQue<DQ>::dqRetSize(){
return dqSize;
}
template <class DQ>
bool DeQue<DQ>::dqIsEmpty(){
if(frontIdx == -1 && rearIdx == -1){
return true;
}else{
return false;
}
}
template <class DQ>
bool DeQue<DQ>::dqIsFull(){
if(dqCap == dqSize){
return true;
}else{
return false;
}
}
template <class DQ>
DQ DeQue<DQ>::dqFront(){
if(dqIsEmpty()){
cout << "DeQue Underflow" << endl;
abort();
}
return dq[frontIdx];
}
template <class DQ>
DQ DeQue<DQ>::dqRear(){
if(dqIsEmpty()){
cout << "DeQue Underflow" << endl;
abort();
}
return dq[rearIdx];
}
template<class DQ>
void DeQue<DQ>::dqPushFront(DQ dQue){
if(dqIsFull()){
dqCap = dqCap*2;
DQ *temp = new DQ[dqCap];
int i = frontIdx, j=0;
while(i != rearIdx){
temp[j++] = dq[i];
i = (i+1) % dqSize;
}
temp[j] = dq[i];
frontIdx = 0;
rearIdx = dqSize - 1;
delete[] dq;
dq = temp;
}
if(dqIsEmpty()){
frontIdx = rearIdx = 0;
dq[rearIdx] = dQue;
dqSize++;
return;
}
frontIdx = (frontIdx - 1 + dqCap) % dqCap;
dq[frontIdx] = dQue;
dqSize++;
return;
}
template <class DQ>
void DeQue<DQ>::dqPushRear(DQ dQue){
if(dqIsFull()){
dqCap = dqCap * 2;
DQ *temp = new DQ[dqCap];
int i = frontIdx, j=0;
while(i != rearIdx){
temp[j++] = dq[i];
i = (i + 1) % dqSize;
}
temp[j] = dq[i];
frontIdx = 0;
rearIdx = dqSize-1;
delete[] dq;
dq = temp;
}
if(dqIsEmpty()){
frontIdx = rearIdx = 0;
dq[rearIdx] = dQue;
dqSize++;
return;
}
rearIdx = (rearIdx + 1) % dqCap;
dq[rearIdx] = dQue;
dqSize++;
return;
}
template <class DQ>
int DeQue<DQ>::dqPopFront(){
int temp;
if(dqIsEmpty()){
cout << "DeQue Underflow" << endl;
abort();
}
if(frontIdx == rearIdx){
temp = dq[frontIdx];
frontIdx = rearIdx = -1;
dqSize--;
return temp;
}
temp = dq[frontIdx];
frontIdx = (frontIdx + 1) % dqCap;
dqSize--;
return temp;
}
template <class DQ>
int DeQue<DQ>::dqPopRear(){
int temp;
if(dqIsEmpty()){
cout << "DeQue Underflow" << endl;
abort();
}
if(frontIdx == rearIdx){
temp = dq[rearIdx];
frontIdx = rearIdx = -1;
dqSize--;
return temp;
}
temp = dq[rearIdx];
rearIdx = (rearIdx - 1 + dqCap) % dqCap;
dqSize--;
return temp;
}
int main(){
DeQue<int> circ_q;
cout << endl << "*****AT EMPTY DEQUE STATE*****" << endl;
cout << "Capacity of the Circular Queue:" << circ_q.dqCapacity() << endl;
cout << "Size of the Circular Queue: " << circ_q.dqRetSize() << endl;
circ_q.dqPushRear(3);
circ_q.dqPushRear(9);
circ_q.dqPushRear(12);
circ_q.dqPushRear(15);
circ_q.dqPushRear(18);
circ_q.dqPushFront(2);
circ_q.dqPushFront(4);
circ_q.dqPushFront(6);
circ_q.dqPushFront(8);
circ_q.dqPushFront(10);
cout << endl <<"*****AFTER INSERTION INTO DEQUE*****" << endl;
cout << "Capacity of the Circular Queue:" << circ_q.dqCapacity() << endl;
cout << "Size of the Circular Queue: " << circ_q.dqRetSize() << endl;
cout << "Front element is: " << circ_q.dqFront() << endl;
cout << "Rear element is: " << circ_q.dqRear() << endl;
cout << endl << "POPPING FRONT ELEMENT" << endl ;
cout << circ_q.dqPopFront() << " SUCCESSFULLY POPPED FROM FRONT"<< endl;
cout << circ_q.dqPopFront() << " SUCCESSFULLY POPPED FROM FRONT"<< endl;
cout << "POPPING REAR ELEMENT" << endl;
cout << circ_q.dqPopRear() << " SUCCESSFULLY POPPED FROM REAR"<< endl;
cout << endl;
cout << "*****AFTER CHANGES*****" << endl;
cout << "Capacity of the Circular Queue:" << circ_q.dqCapacity() << endl;
cout << "Size of the Circular Queue: " << circ_q.dqRetSize() << endl;
cout << "Front element is: " << circ_q.dqFront() << endl;
cout << "Rear element is: " << circ_q.dqRear() << endl;
return 0;
}

You can also try this code with Online C++ Compiler
OUTPUT:
*****AT EMPTY DEQUE STATE*****
Capacity of the Circular Queue:4
Size of the Circular Queue: 0
*****AFTER INSERTION INTO DEQUE*****
Capacity of the Circular Queue:16
Size of the Circular Queue: 10
Front element is: 10
Rear element is: 18
POPPING FRONT ELEMENT
10 SUCCESSFULLY POPPED FROM FRONT
8 SUCCESSFULLY POPPED FROM FRONT
POPPING REAR ELEMENT
18 SUCCESSFULLY POPPED FROM REAR
*****AFTER CHANGES*****
Capacity of the Circular Queue:16
Size of the Circular Queue: 7
Front element is: 6
Rear element is: 15
Complexities
Time Complexity
The time complexity of the given implementation is O(N) since every time we double the deque, we copy all of its elements into the new deque. Thus, T(n) = O(N)
Space Complexity
The space complexity of the given implementation is O(N). This is the extra space used by the program while copying the deque elements. Thus, Space Complexity = O(N)
Check out this problem - Queue Implementation
Frequently Asked Questions
What are the other ways of implementing Deque?
We can use a doubly-linked list to implement Deque. In that case, we will have to maintain the front and rear pointers.
What is the application of a Deque?
A deque can be used in the work-stealing algorithm. This algorithm is used for task scheduling for several processors.
Conclusion
To summarize the article, we discussed implementing dynamic deque using the templates class and a circular array. We saw the problem statement, an example, the approach to the problem, along with its explanation. We saw the solution code and output along with the time and space complexities.
Improve your coding skills by practicing various problems of various difficulty levels on our Coding Ninjas Studio.
Recommended Readings:
Do check out The Interview guide for Product Based Companies as well as some of the Popular Interview Problems from Top companies like Amazon, Adobe, Google, Uber, Microsoft, etc. on Coding Ninjas Studio.
Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Operating Systems, Computer Networks, DBMS, System Design, Basics of C++, Basics of Java, Basics of Python, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.
Happy Coding!