Example
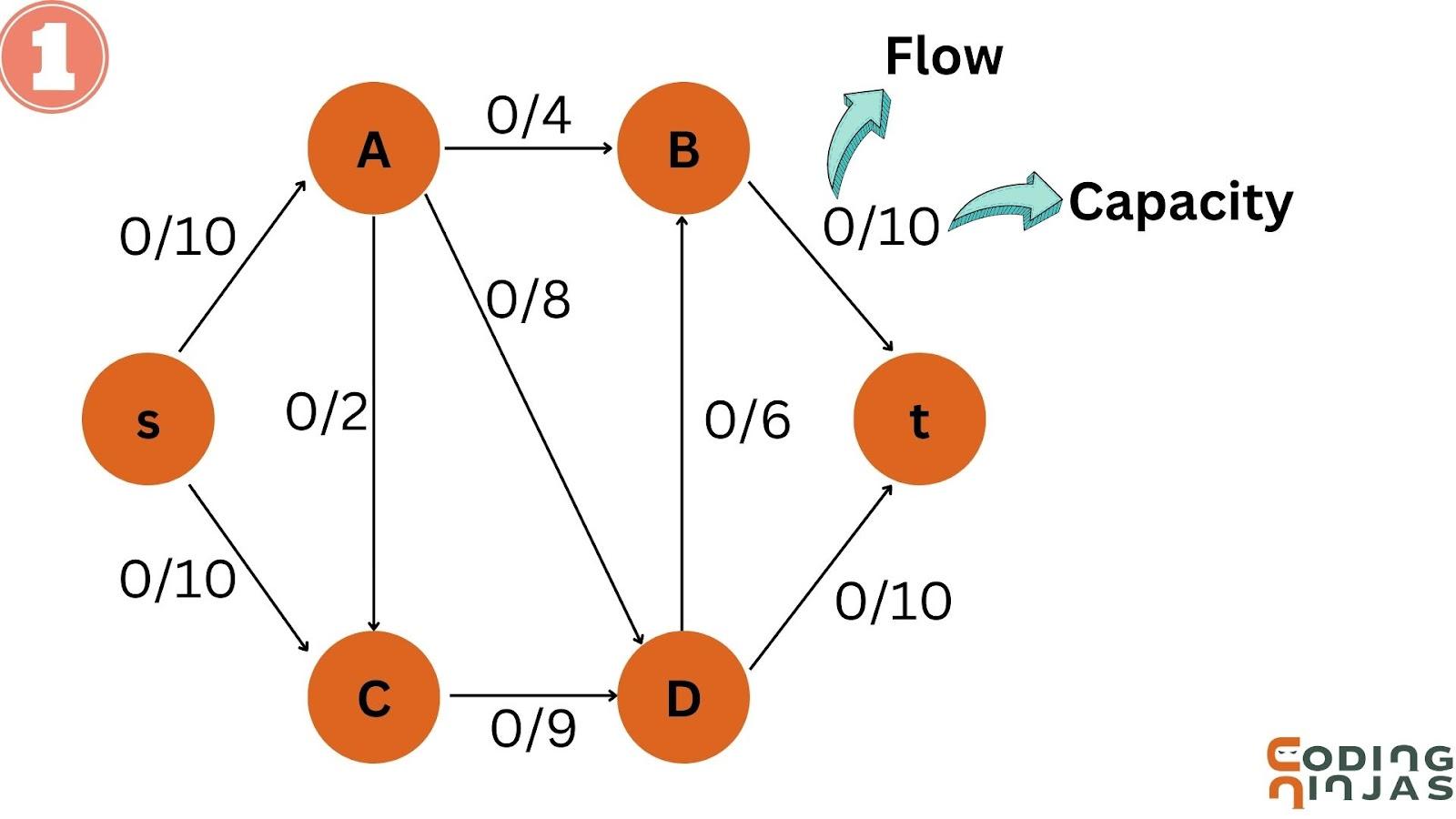
Consider the following graph where S= Source and T= Sink.
Initially the Flow=0
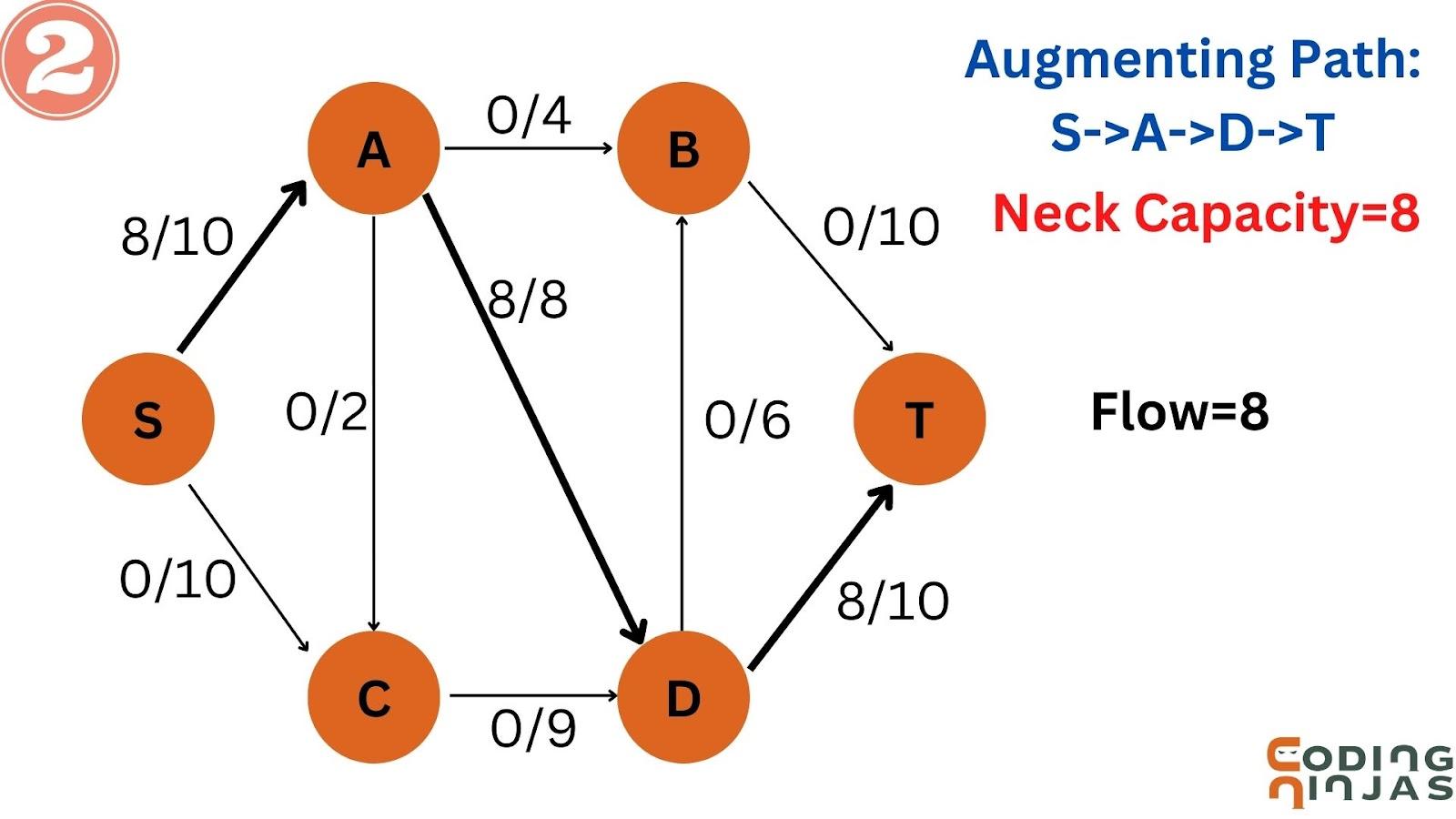
Let's take an augmenting path S->A->D->T and the neck capacity=8.
So. update the values of this augmenting path.
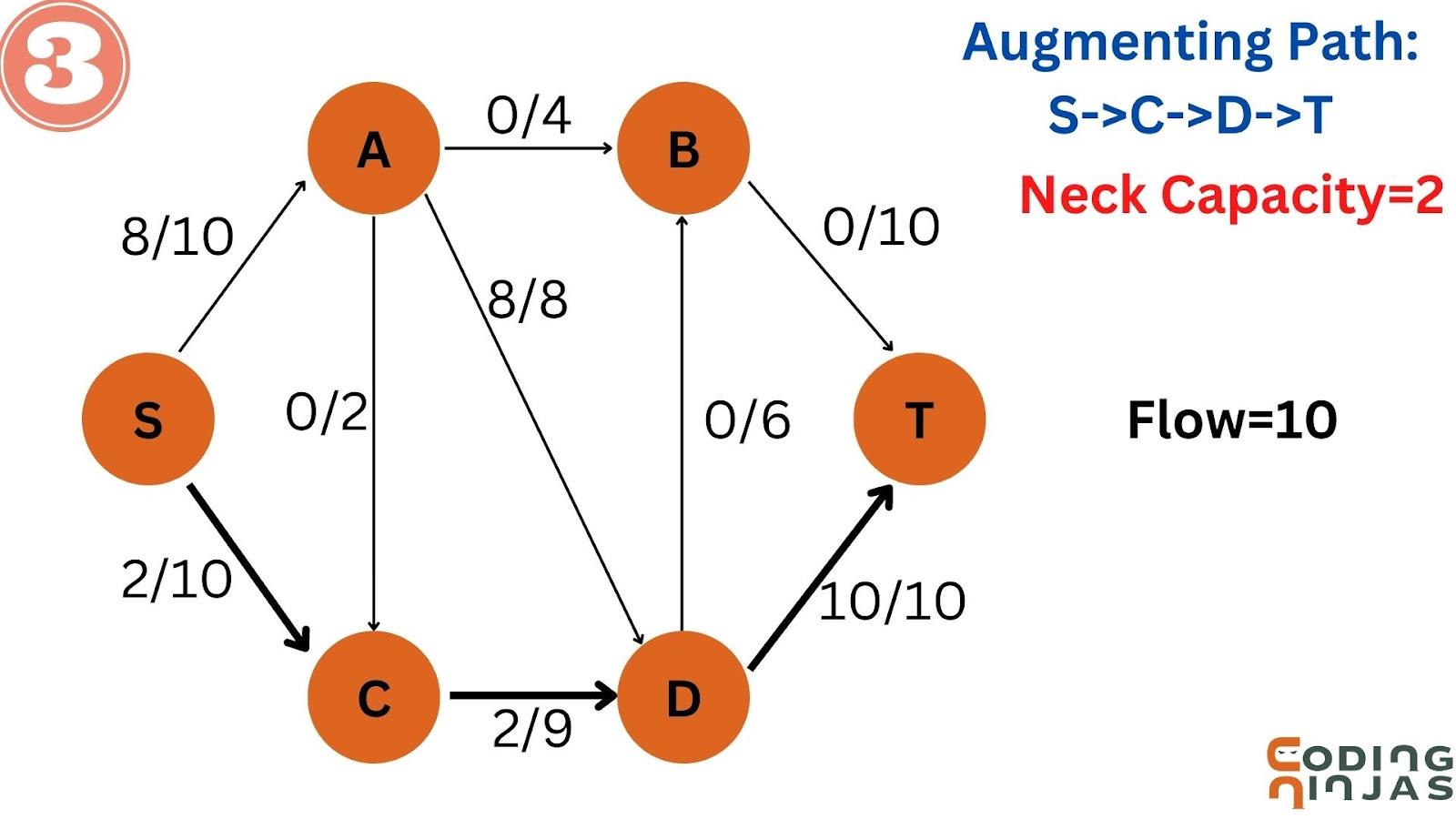
Take an augmenting path S->C->D->T, and the neck capacity=2.
Then, update the values of this augmenting path.
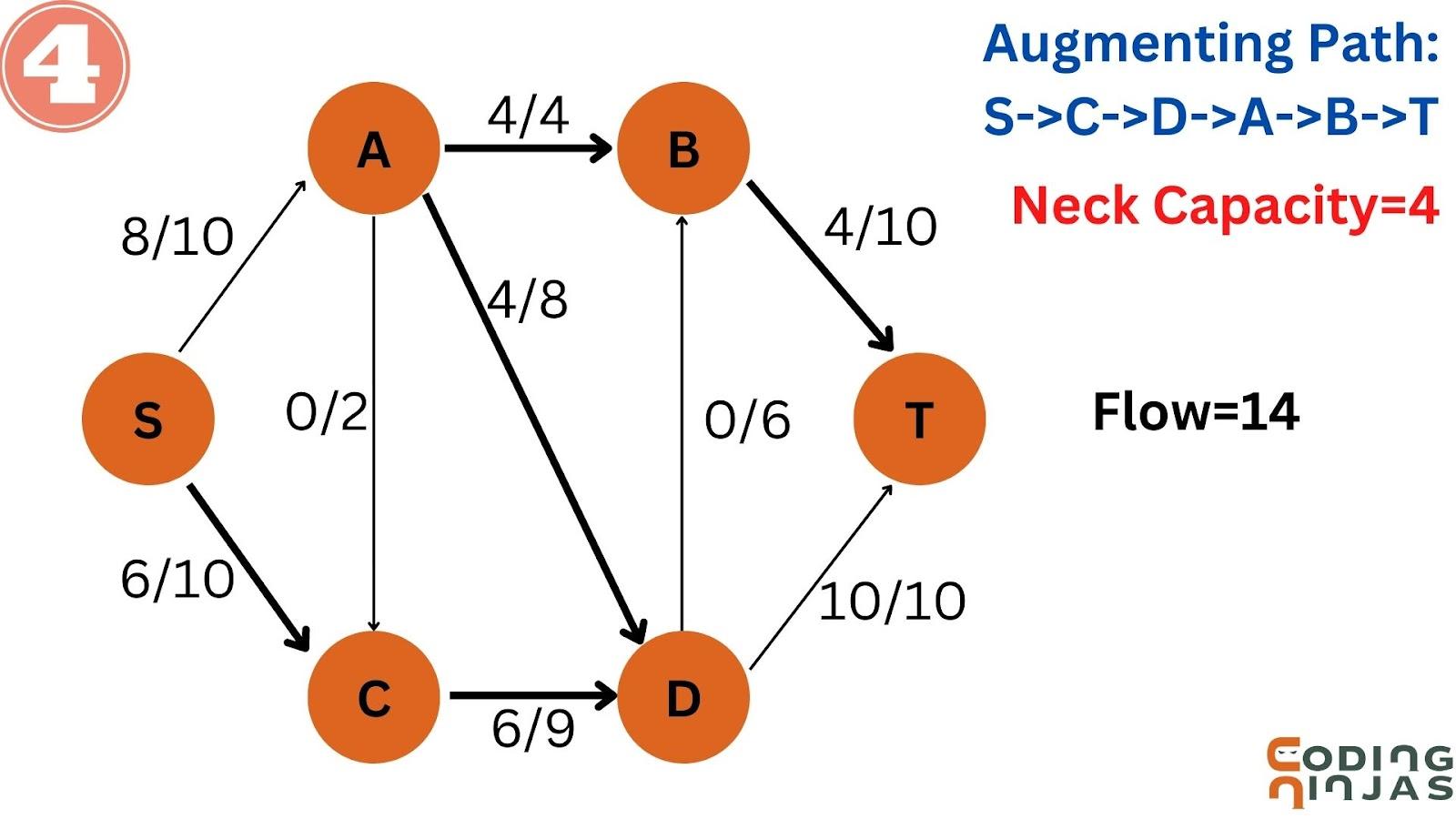
Take an augmenting path S->C->D->A->B->T and the neck capacity=4.
Then, update the values of this augmenting path.
Take an augmenting path S->A->D->B->T and the neck capacity=2.
Then, update the values of this augmenting path.
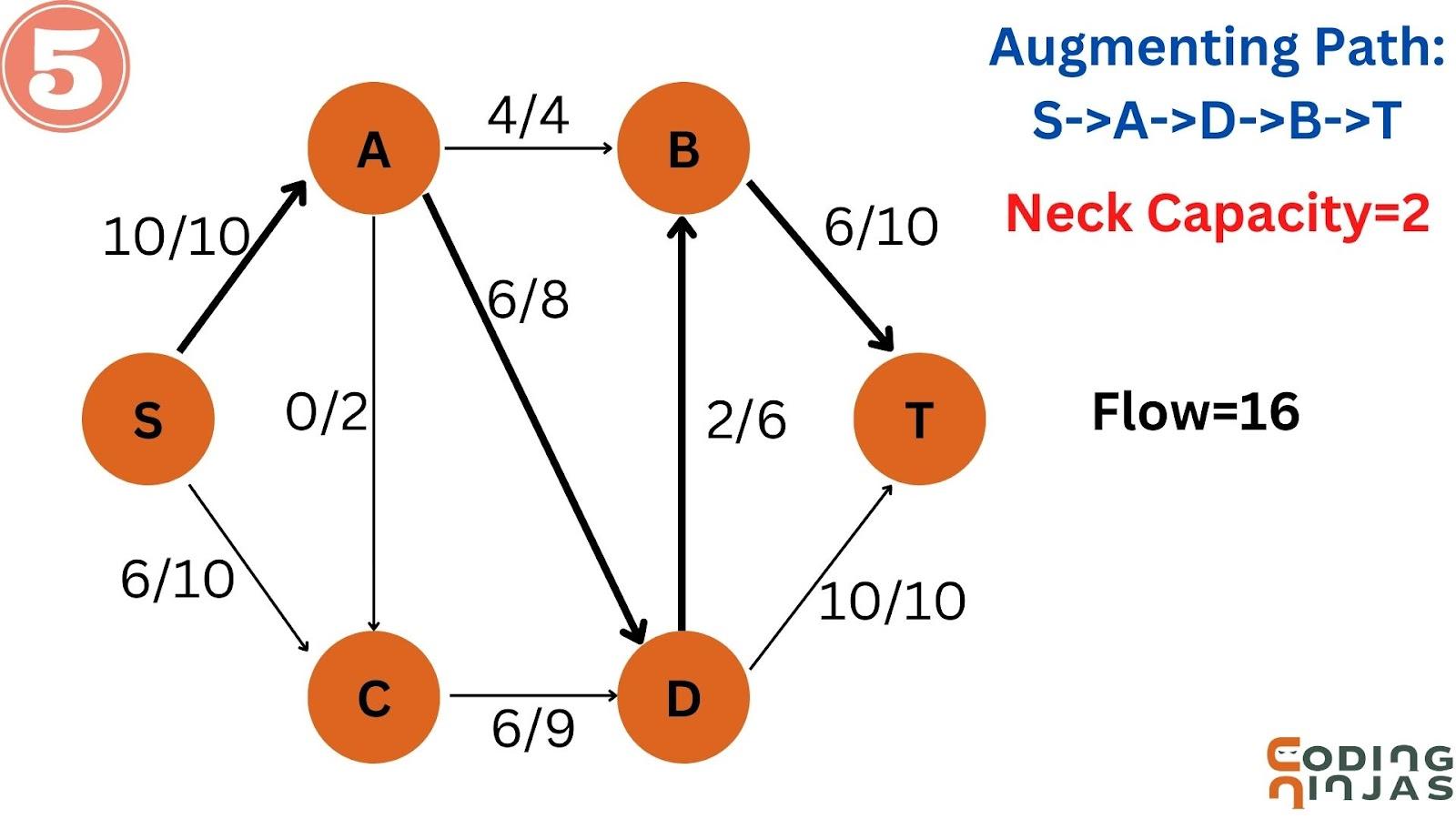
Take an augmenting path S->C->D->B->T and the neck capacity=3.
Then, update the values of this augmenting path.
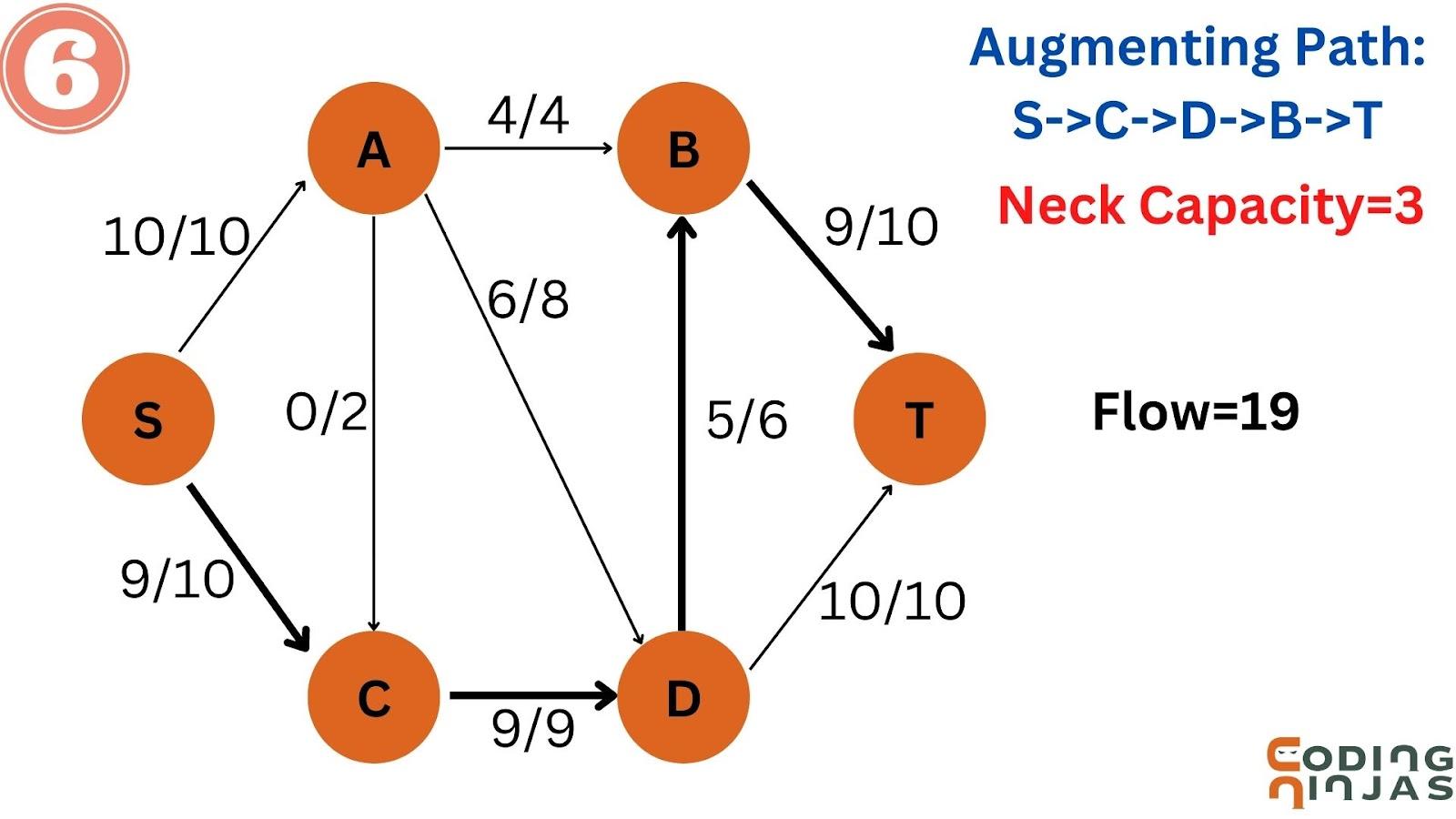
Hence, The flow=19.
Let's discuss the algorithm.
Algorithm
The algorithm is entirely based on the following three operations.
- Initialize the graph with a preflow and the labelling functions with each edge outgoing from s with its maximal capacity and all other edges with zero.
- Push() - We push as much excess flow from one Vertex u to a neighboring vertex v.
- Relabel() - We will increase the Vertex's height when we cannot push the excess to any adjacent vertex. Also, we can expand it by as much as possible while still maintaining the validity of the labeling.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
struct Edge
{
int flow;
int capacity;
int u, v;
Edge(int flow, int capacity, int u, int v)
{
this->flow = flow;
this->capacity = capacity;
this->u = u;
this->v = v;
}
};
struct Vertex
{
int height, e_flow;
Vertex(int height, int e_flow)
{
this->height = height;
this->e_flow = e_flow;
}
};
// To represent a flow network
class Graph
{
int V;
vector<Vertex> vertex;
vector<Edge> edge;
bool push(int u);
void relabel(int u);
void preflow(int source);
void ReverseEdgeFlowUpdate(int i, int flow);
public:
Graph(int V);
void addEdge(int u, int v, int w);
int getMaximumFlow(int source, int sink);
};
Graph::Graph(int V)
{
this->V = V;
for (int i = 0; i < V; i++)
vertex.push_back(Vertex(0, 0));
}
// To push flow from overflowing Vertex u
bool Graph::push(int u)
{
for (int i=0; i <edge.size(); i++)
{
if (edge[i].u == u)
{
if (edge[i].flow == edge[i].capacity)
continue;
if (vertex[u].height > vertex[edge[i].v].height)
{
int flow = min(edge[i].capacity - edge[i].flow,
vertex[u].e_flow);
vertex[u].e_flow = vertex[u].e_flow-flow;
vertex[edge[i].v].e_flow = vertex[edge[i].v].e_flow + flow;
edge[i].flow = edge[i].flow + flow;
ReverseEdgeFlowUpdate(i, flow);
return true;
}
}
}
return false;
}
// function to Relabel vertex u
void Graph::relabel(int u)
{
int maximum_height = INT_MAX;
int n=edge.size();
// To Find the adjacent with minimum height
for (int i = 0; i < n; i++)
{
if (edge[i].u == u)
{
if (edge[i].flow == edge[i].capacity)
continue;
// for Updating the minimum height
if (vertex[edge[i].v].height < maximum_height)
{
maximum_height = vertex[edge[i].v].height;
// updating the height of u
vertex[u].height = maximum_height + 1;
}
}
}
}
void Graph::preflow(int source)
{
vertex[source].height = vertex.size();
int n=edge.size();
for (int i = 0; i < n; i++)
{
if (edge[i].u == source)
{
edge[i].flow = edge[i].capacity;
// Initialize excess flow for adjacent v
vertex[edge[i].v].e_flow = vertex[edge[i].v].e_flow + edge[i].flow;
edge.push_back(Edge(-edge[i].flow, 0, edge[i].v, source));
}
}
}
void Graph::addEdge(int u, int v, int capacity)
{
edge.push_back(Edge(0, capacity, u, v));
}
// To Update reverse flow for flow added on ith Edge
void Graph::ReverseEdgeFlowUpdate(int i, int flow)
{
int u = edge[i].v;
int v = edge[i].u;
int j=0, n=edge.size();
while (j < n)
{
if (edge[j].v == v && edge[j].u == u)
{
edge[j].flow -= flow;
return;
}
j++;
}
// adding the reverse Edge in the residual graph
Edge e = Edge(0, flow, u, v);
edge.push_back(e);
}
//Function to return an index of overflowing Vertex
int overFlowVertex(vector<Vertex>& vertex)
{
int n=vertex.size();
for (int i = 1; i < n - 1; i++)
if (vertex[i].e_flow > 0)
return i;
return -1;
}
// The main function is to print the maximum flow of the graph
int Graph::getMaximumFlow(int source, int sink)
{
preflow(source);
while (overFlowVertex(vertex) != -1)
{
int u = overFlowVertex(vertex);
if (!push(u))
relabel(u);
}
return vertex.back().e_flow;
}
// Driver Code
int main()
{
int V = 6;
Graph g(V);
g.addEdge(0, 1, 10);
g.addEdge(0, 3, 10);
g.addEdge(1, 3, 2);
g.addEdge(1, 2, 4);
g.addEdge(1, 4, 8);
g.addEdge(3, 4, 9);
g.addEdge(2, 5, 10);
g.addEdge(4, 5, 10);
g.addEdge(4, 2, 6);
int source = 0, sink = 5;
cout << "Maximum flow is " << g.getMaximumFlow(source, sink);
return 0;
}

You can also try this code with Online C++ Compiler
Output:
The maximum flow is 19
Complexity Analysis
Time Complexity: There will be at most O(VE) saturating and O(V^2E) non-saturating pushes.
Saturating pushes means a push where the total capacity of an edge is used. Non-saturating pushes a push where the total capacity of an edge is partially used. If we find the next Vertex with excess O(1) time, the overall time complexity is O(V^2E).
Also Read - Kadanes Algorithm
Now, let's discuss FAQs related to the Push Relabel Algorithm.
Frequently Asked Questions
What do you mean by Push Relabel Algorithm, and What was the reason behind naming it as Push Relabel Algorithm?
Push Relabel Algorithm is an algorithm to find the maximum flow of a flow network.
In the "Push Relabel Algorithm," Push, and Relabel is the two primary functions of this algorithm.
What is Push Relabel Algorithm commonly known?
Push Relabel Algorithm is commonly known as Maximum flow or preflow Push Relabel Algorithm.
Name another algorithm that is similar to the Push Relabel Algorithm.
Ford-Fulkerson algorithm is similar to the Push Relabel Algorithm. It requires O(E^2V) time complexity which is more than the Push Relabel Algorithm, which requires O(V^2E).
What is Graph?
A graph is a non-linear data structure. It consists of vertices and edges.
Conclusion
We have discussed the Implementation of the Push Relabel Algorithm. We have also addressed the problem statement with the algorithm. At last, we have seen their time complexity and some related FAQs.
After reading about the Implementation of the Push Relabel Algorithm, are you not feeling excited to read/explore more articles on Data Structures and Algorithms? Don't worry; Coding Ninjas has you covered. See Graph, Binary Tree, BFS vs DFS, Check for Balanced Parentheses in an Expression, and Stack to learn.
Refer to our Guided Path on Coding Ninjas Studio to upskill yourself in Data Structures and Algorithms, Competitive Programming, JavaScript, System Design, and many more!
Do upvote our blogs if you find them helpful and engaging!
Happy Learning!












