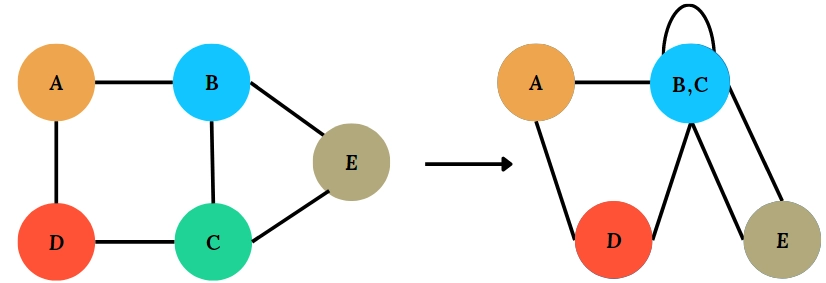
Algorithm
- Make a copy of graph G, termed a contracted graph.
-
While contracted graph contains more than two vertices, i.e., while(v > 2)
- Select any random edge from ‘u’ to ‘v’ of this contracted graph.
- Merge the vertices ‘u’ and ‘v’ into a supernode and compress the edge.
- Remove loops (if formed).
- After the end of the while loop, only two vertices are left, and the edges connecting those two vertices represent the minimum cut of the graph.
Example
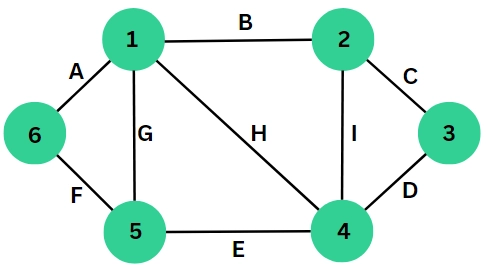
Take an undirected graph having six vertices and nine edges.
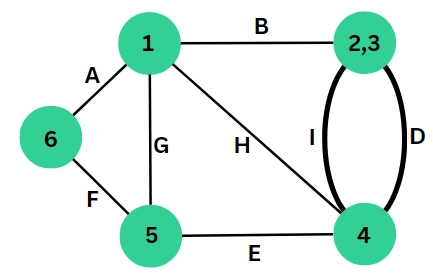
Step 1: Combine vertex 2 and 3 by compressing edge C. Then adjust other edges accordingly.
Step 2: Combine vertex 1 and 4 by compressing edge H. Then adjust other edges accordingly.
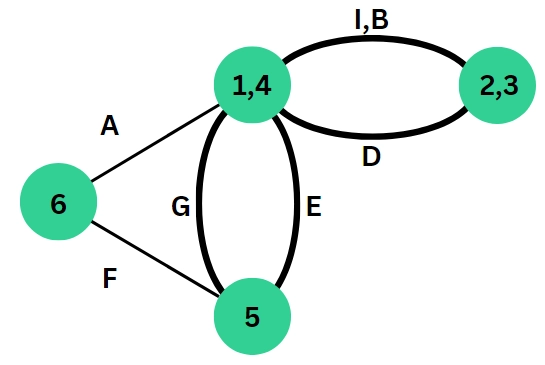
Step 3: Combine vertex 2,3 and 5 by compressing edges G and E. Then adjust other edges accordingly.
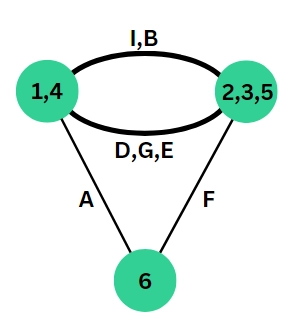
Step 4: Now combine vertices 1,4 and 2,3,5 to make one supernode of all {1,2,3,4,5} you can remove the edge A and F to make the graph disconnected to divide into two components.
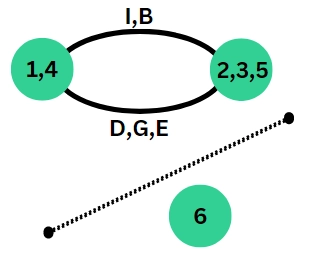
Step 5: Two components of the graph will be separated as follows:
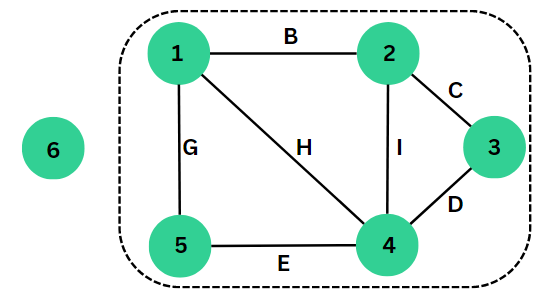
Below, the program shows the implementation part of implementations and applications of Karger’s algorithm for minimum cut.
Implementation
#include<bits/stdc++.h>
using namespace std;
// Creating edge class
class Edge{
public:
// Declaring endpoints u and v
int u;
int v;
//Constructor
Edge(){};
// Creating constructor for giving values
Edge(int U,int V)
{
u=U;
v=V;
}
};
// Creating class for the minimum cut
class MinCut{
public:
int V, E;
int *parent;
int *r;
// Constructor for giving value
MinCut(int v, int e){
V=v;
E=e;
parent=new int[V];
r=new int[V];
// Initializing parent and rank (r)
for(int i=0;i<V;i++)
{
parent[i]=i;
r[i]=0;
}
}
// Function to find minimum using karger algorithm.
int minCutKarger(Edge edges[]){
int vertices=V;
// Run loop till vertices is greater than 2.
while(vertices>2)
{
// Generating a random integer
int rd = rand()%E;
// Finding leader element of edges[rd].u belongs.
int set1=find(edges[rd].u);
// Finding leader element of edges[rd].v belongs.
int set2=find(edges[rd].v);
// Print the edge if they belong to a different set.
if(set1 != set2)
{
cout<<"\nVertices to be combined - "<<edges[rd].u<<" and "<<edges[rd].v;
// Making supernode of vertices u and v
Supernode(edges[rd].u,edges[rd].v);
// Decrement vertex value.
vertices--;
}
}
cout<<"\n\nEdges removed - "<<endl;
// Initializing answer (minCut) to 0.
int ans=0;
for(int i=0;i<E;i++)
{
// Finding leader element of edges[rd].u belongs.
int set1=find(edges[i].u);
// Finding leader element of edges[rd].v belongs.
int set2 =find(edges[i].v);
// If they belong to a different set, then print edges.
if(set1!=set2)
{
cout<<edges[i].u<<" <----> "<<edges[i].v<<endl;
// Increment ans variable.
ans++;
}
}
return ans;
}
// Function to fint the node
int find(int node){
// Compare the parent node and the root node.
if(node==parent[node]) return node;
// Else, compress the edges.
return parent[node] = find(parent[node]);
}
// Function to make supernode
void Supernode(int u , int v){
u = find(u);
v = find(v);
// Compare u and v. They belong to the same tree if they are equal.
if(u!=v)
{
// Finding trees with smaller depths.
if(r[u]<r[v])
{
int temp=u;
u=v;
v=temp;
}
// Attaching the lower rank tree to the higher one.
parent[v]=u;
// If now ranks are equal, increasing the rank of u.
if(r[u]==r[v])
r[u]++;
}
}
};
int main(){
int V=5,E=8;
// Create an Object of class MinCut.
MinCut obj(V,E);
// Creating an array of edges.
Edge *edge=new Edge[E];
// Creating graph
edge[0]=Edge(0,4);
edge[1]=Edge(0,5);
edge[2]=Edge(0,1);
edge[3]=Edge(5,3);
edge[4]=Edge(1,2);
edge[5]=Edge(1,3);
edge[6]=Edge(3,2);
edge[7]=Edge(2,4);
// Finding the size of the minimum cut.
int count = obj.minCutKarger(edge);
cout<<"\nNo of edges removed = "<<count;
return 0;
}

You can also try this code with Online C++ Compiler
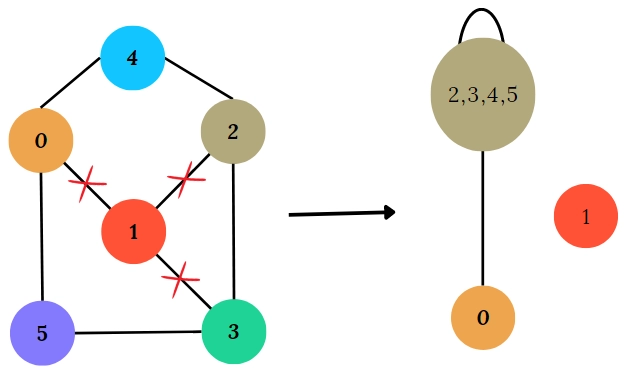
Representation of graph taken in implementation
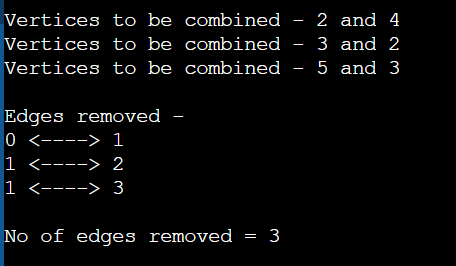
Output
Let’s now discuss the complexities of the implementations and applications of Karger’s algorithm for minimum cut.
Complexity Analysis
Time Complexity
The time complexity of Karger’s algorithm is O( E * α(V) ) where (α = alpha) for a graph G having V vertices and E edges because, in every iteration, you are contracting the edges by creating supernodes in the contracted graph.
And in terms of the number of vertices, the time complexity is O(V^2).

Explanation:
As for V<10^600, O(α(V)) is approximately equal to O(1). So, O(E∗α(V)) = O(E * 1), and the maximum number of edges in a graph is the order of V^2; therefore, O(E) = O(V^2).
Space Complexity
O(V), where V is the size of the array.
Explanation: Storing all the array elements consumes O(V) space.
We have already discussed the implementation part, now discuss the application part of “Implementations and Applications of Karger’s algorithm for Minimum Cut”.
Applications
- It can be used to study network reliability, i.e., the smallest number of links that can cause the failure of the entire network.
- It is used in recommendation systems.
- Split large graphs into smaller ones to ease the computation.
- It is used to segment an image, i.e., separating the foreground and background of an image.
- It is used for detecting weak ties in a graph.
- In wartime, it is used to know the minimum number of roads needed to be destroyed to block connectivity.
Frequently Asked Questions
What is a cut in graph theory?
A cut refers to the partition of vertices of a graph into two or more disjoint subsets.
What is the minimum cut?
Minimum cut is defined as the minimum number of edges, when removed from a graph, divide the graph into two disjoint sets.
What are disjoint sets?
Two sets are called disjoint sets if the intersection of two sets is NULL. A Disjoint-Set data structure that keeps records of a set of elements partitioned into several non-overlapping (Disjoint) subsets.
Why does the Karger algorithm give the wrong output?
The Karger algorithm is a “Monte Carlo” algorithm based on random outcomes. So it can also give wrong answers.
What does edge contraction mean?
Edge contraction means merging two nodes (say u and v) of the graph G into one node, also termed a supernode.
Conclusion
The above blog covers the implementations and applications of Karger’s algorithm for minimum cut. We discussed what Karger’s algorithm is and what is the time and space complexity of the algorithm.
After reading this article on the implementations and applications of Karger’s algorithm for minimum cut, you might want to read other related articles. So below are the links for the same:
Please refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. And also, enroll in our courses and refer to the mock test and problems available. Have a look at the interview experiences and interview bundle for placement preparations. Nevertheless, you may consider our paid courses to give your career an edge over others!
Happy Coding!