Introduction
A binary tree is a type of tree data structure. It contains a single root node and two disjoint subtrees called the left and the right subtree. The maximum degree of the node of a binary tree is 2. A binary search tree is a tree data structure that uses some order to arrange its elements, whereas a binary tree does not. You can visit our articles, Binary Tree and Binary Search Tree, to learn more about binary trees and BST.

This article will discuss the problem of implementing decrease key in BST. We will use the deletion and insertion key approach for implementing decrease key in BST.
Problem Statement
The problem is of implementing decrease key in BST. We are given a BST. We will write a function that takes three arguments. The root of the tree, the old key value, and the new key value.

The function we make should change the old key value to the new key value. The function can assume that the old key value always exists in BST. Now, let’s understand the problem of implementing the decrease key in BST with some examples.
Samples Examples
Example 1:
Input: The root of the below tree.

Old key value: 35
New key value: 5
Output:
Updated BST

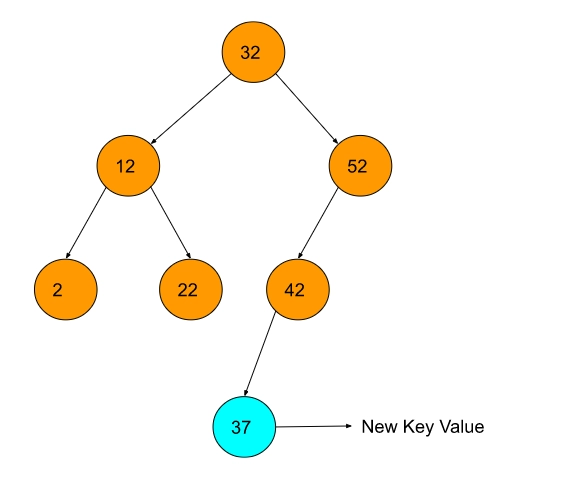
Example 2:
Input: The root of the below tree

Old key value: 72
New key value: 37
Output: Updated BST
Check out this problem - Mirror A Binary Tree
Deletion and Insertion Key Approach
We have the deletion and insertion key approach for implementing the decrease key in BST. The idea behind this approach is to call delete for the old key value. Then we will call insert for the new key value. Let’s see the algorithm for this approach.
Algorithm
- We will make a function to create a BST node.
- Afterward, we will make a function to do an in-order traversal of BST.
- Now create a function to insert a new node with a given key in BST. To do so, we will make two cases. First, if the tree is empty. Then return a new node. Otherwise, recur down the tree. And now, return the node pointer.
- When we are provided with a non-empty binary search tree. We will return the node with the minimum key value found in that tree. The entire tree will not be searched.
-
If we are provided with a BST and a key. The function deletes the key and returns the new root.
- If the key which will be deleted is smaller than the root's key, then it lies in the left subtree.
- If the key which will be deleted is greater than the root's key, then it lies in the right subtree.
- If the key is the same as the root's key, then that is the node supposed to be deleted.
Implementation
// Program of implementing decrease key on bst
#include<bits/stdc++.h>
using namespace std;
struct node
{
int key;
node *left, *right;
};
// The function to create a new BST node
node *newNode(int element)
{
node *temp = new node;
temp->key = element;
temp->left = temp->right = NULL;
return temp;
}
// A function to do in order traversal of BST
void inordertraversal(node *rootnode)
{
if (rootnode != NULL)
{
inordertraversal(rootnode->left);
cout << rootnode->key << " ";
inordertraversal(rootnode->right);
}
}
// Given a non-empty bst, return the node with minimum key found in tree.
node * minimumValueNode(node* Node)
{
node* present= Node;
// looping down to find the leftmost leaf
while (present->left != NULL)
present= present->left;
return present;
}
// A function to insert a new node with given key in BST
node* insertkey(node* node, int key)
{
// If the tree is empty then we will return a new node
if (node == NULL)
return newNode(key);
// Otherwise we will recur down the tree
if (key < node->key)
node->left = insertkey(node->left, key);
else
node->right = insertkey(node->right, key);
return node;
}
// Given a bst and a key, this function deletes the key and returns the new root
node* deletenodekey(node* rootnode, int key)
{
if (rootnode == NULL)
return rootnode;
// Now if the key to be deleted is smaller than the root's key, then it lies in the left subtree
if (key < rootnode->key)
rootnode->left = deletenodekey(rootnode->left, key);
// And if the key to be deleted is greater than the root's key, then it lies in the right subtree
else if (key > rootnode->key)
rootnode->right = deletenodekey(rootnode->right, key);
// if the key is the same as root's key. Then the node to be deleted is
else
{
// node with only one or no child
if (rootnode->left == NULL)
{
node *tempvar = rootnode->right;
free(rootnode);
return tempvar;
}
else if (rootnode->right == NULL)
{
node *tempvar = rootnode->left;
free(rootnode);
return tempvar;
}
// node with two children. Here, Get the inorder successor (smallest in the right subtree)
node* tempvar = minimumValueNode(rootnode->right);
// Now Copy the inorder successor's content to this node
rootnode->key = tempvar->key;
// Delete the inorder successor
rootnode->right = deletenodekey(rootnode->right, tempvar->key);
}
return rootnode;
}
// The function to decrease a key value in Binary Search Tree
node *changingtheKey(node *rootnode, int oldVal, int newVal)
{
// First delete old key value
rootnode = deletenodekey(rootnode, oldVal);
// Then insert new key value
rootnode = insertkey(rootnode, newVal);
// Return new root
return rootnode;
}
int main()
{
int keys[] = { 45, 25, 15, 35, 65, 55, 75 };
node* rootnode = nullptr;
for (int key: keys) {
rootnode = insertkey(rootnode, key);
}
cout << "Inorder traversal of given tree \n";
inordertraversal(rootnode);
rootnode = changingtheKey(rootnode, 35, 5);
cout << "\nInorder traversal of the modified tree \n";
inordertraversal(rootnode);
return 0;
}
Output:

Time Complexity
The above approach's time complexity for implementing the decrease key in BST is O(h). Here h is the height of BST.
Space Complexity
The space complexity of the above approach for the problem implementing decrease key in BST is O(n). Here we used extra space to store nodes. The algorithm used for conversion has a linear space complexity. Hence, the space complexity of the approach is O(n).
You can also read about insertion into bst.




