Approach
The approach to implementing a Forward BST iterator is to use a stack data structure to store the left nodes of the root node in the stack, and while popping every node, we have to check that if the node has the right subtree again, push that right node to stack which will ultimately store the elements in ascending order in the stack.
Algorithm
- Make a private stack in the BstIForwardIerator class named as ‘st’, which will store the nodes of the BST.
- Make a ‘pushAllLeftNodes()’ function with parameter as the root node, which will push the current node into the stack and all the left nodes for the given node.
- Do node = node->left till the current node doesn't go to a null pointer which will ultimately push all left nodes in the stack, and the same is also done in the inorder traversal.
- For the current node, return the topmost pointer of the stack.
- For the next pointer, we have to return the next greater element in the right subtree of the current node, so for that, we will pop the current node from the stack and use the pushAllLeftNodes function to push the right part of the current node.
- To check whether we have the next node or not, check the size of the stack. If the stack is empty, there is no more node left to traverse. Else return true.
- Make all these functions public in the BST iterator to access these functions from the outside of the class.
Code
#include <bits/stdc++.h>
using namespace std;
// Binary TreeNode structure
class TreeNode {
public :
int value;
TreeNode* left;
TreeNode* right;
TreeNode(int value)
{
this->value = value;
left = NULL;
right = NULL;
}
};
// Implementing design of BST iterator
class BstIForwardIerator{
Private:
// Stack to store the nodes
stack<TreeNode*> St;
Public:
// Constructor for the class
BstIForwardIerator(TreeNode *root) {
pushAllLeftNodes(root);
}
// Returning the current element for BSTiterator
TreeNode* curr()
{
return St.top();
}
// Increase the count of iterator to next element
void next()
{
TreeNode *tempNode = St.top();
St.pop();
pushAllLeftNodes(tempNode->right);
}
// Function to check that if we are at end of BST or not
bool isEnd()
{
return !(St.size());
}
Private:
// Function to push all left nodes for an current iterator
void pushAllLeftNodes(TreeNode *node) {
for (; node != NULL; St.push(node), node = node->left);
}
};
// Function for iterating on the tree
void iterate(BstIForwardIerator tree)
{
while (!tree.isEnd())
{
cout << tree.curr()->value << " ";
tree.next();
}
}
int main()
{
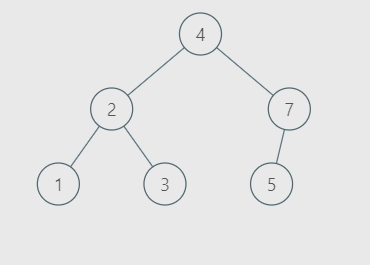
TreeNode * root = new TreeNode(4);
root->left = new TreeNode(2);
root->right = new TreeNode(7);
root->left->left = new TreeNode(1);
root->left->right = new TreeNode(3);
root->right->left = new TreeNode(5);
// Formation of object of BST iterator
BstIForwardIerator tree(root);
// Function to test BST iterator
iterate(tree);
return 0;
}

You can also try this code with Online C++ Compiler
Output:
1 2 3 4 5 7
Time Complexity
O(1)
The time complexity to implement Forward BST iterator will be O(1) that is constant time on average of total calls. Sometimes we are pushing left of the nodes, and sometimes we are not pushing. So on average, that is if there are a total of N nodes and if there are ‘N’ next calls in the BST iterator, then the average time complexity will be ~(N/N) ~O(1)
Space Complexity
O(H)
The space complexity to implement Forward BST iterator will be O(H), where ‘H’ is the height of the Binary search tree because the stack stores all the left nodes at a given instant of time. It is not storing all the nodes of BST. Simultaneously for every next call, the current node is popped out of the stack, so it will take an average of height complexity at max.
You can also read about insertion into bst.
Frequently Asked Questions
What is a stack?
Stack is a data structure that stores elements in LIFO format that is last in first out format and the operations are performed in a particular order to know more about stack refer to this link stack.
What is a Binary search tree?
A generic tree with at most two child nodes for every node, the left subtree has a value less than the root node, and the right subtree has a value greater than the root node.
Is there any other way to design a BST iterator?
Yes, we can store the entire inorder traversal of BST in a vector. We can maintain a pointer that will tell the current position and check for the next element in constant time complexity but, it will cost o(n) space complexity where ‘n’ is the number of nodes. At the same time, this stacking approach will take O(H) space complexity.
Conclusion
In this blog, we designed a Forward BST iterator, a low-level design for iterating in a Binary search tree with a lot of functions to check the next element in the BST or to check the current element.
If you want to learn more about Binary search trees and stacks and want to practice some questions which require you to take your basic knowledge on these topics a notch higher, then you can visit our Guided Path for arrays on Coding Ninjas Studio.To be more confident in data structures and algorithms, try out our DS and Algo Course.
Recommended Reading:
Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Operating Systems, Computer Networks, DBMS, System Design, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.
Cheers!