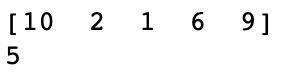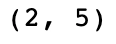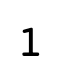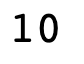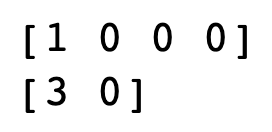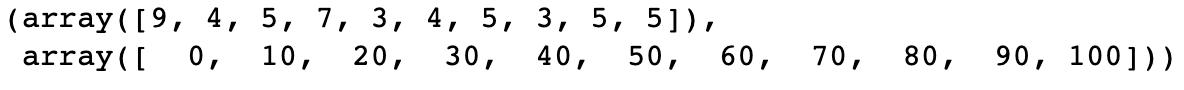List of Numpy Functions in Python
A list of Important Numpy Functions in Python are -
(i) Numpy.linspace()
(ii) Numpy.repeat()
(iii) Numpy.random()
(iv) Numpy.nan()
(v) Numpy.argmax()
(vi) Numpy.histogram()
(vii) Numpy.min(), Numpy.max()
(viii) NUmpy.mean()
(ix) Numpy.shape()
(x) Numpy.reshape()
(xi) Numpy.sort()
NumPy.linspace
This function returns a list of numbers spaced evenly over the specified interval.
numpy.linspace(start, stop, num=50, endpoint=True,dtype=None axis=0)
→ start - refers to the beginning of the interval range.
→ stop - refers to the end of the interval range.
→ Num - refers to the number of samples generated.
→ Endpoint - refers to the defined endpoint, if any.
→ dtype - refers to the datatype of the newly generated array.
→ Axis - refers to along rows if '1' and along columns if '0'.
NOTE: if 'num' is not defined, then automatically, 50 samples are generated.
#numpy.linspace()
list1= np.linspace(start=0, stop=8, num=5, dtype=int, axis=0, endpoint=True)
print(list1)
print(" ")
list2= np.linspace(start=0, stop=10, dtype=float, axis=0)
print(list2)
Output
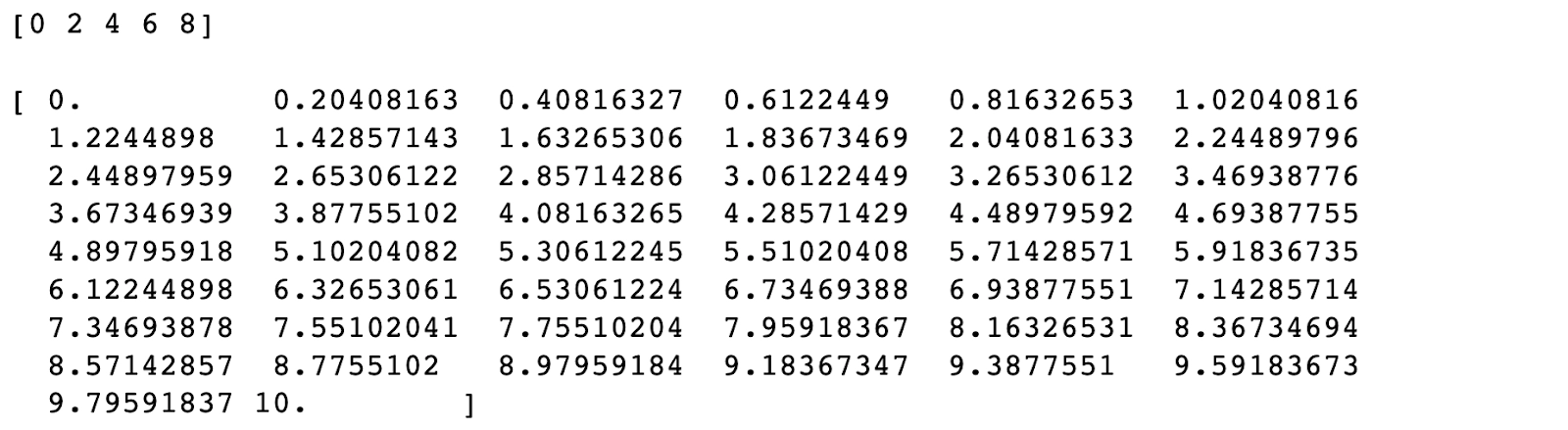
-> In the first example, we get a list of evenly spaced numbers in the specified range.
-> In the second example, we notice that since we have not defined the parameter 'num,' we get 50 samples automatically.
NumPy.repeat()
This function repeats the elements of the array passed as its argument and returns a newly generated array.
numpy.repeat(arr, repetitions, axis = None)
→ Arr - refers to the input array.
→ Repetitions - refers to the no. of repetitions of each array element.
→ Axis - refers to the axis along which we wish to return values.
#numpy.repeat()
arr1 = [1,2,3,4,5]
list1= np.repeat(arr1, 2, axis=0)
print(list1)
print(" ")
arr2=[[1,2,3],[4,5,6]]
#along columns since axis is 0
list2= np.repeat(arr2, 2, axis=0)
print(list2)
print(" ")
#along rows since axis is 1
list3= np.repeat(arr2, 2, axis=1)
print(list3)
Output

-> In the first example, we notice that on passing repetition as 2, we get a newly generated array in which each element of the initial array is repeated.
-> In the second example, we notice that on passing the axis as 0, we get a newly generated 2-D array (matrix) in which each element of the initial array is repeated along the columns.
-> In the third example, we notice that on passing the axis as 1, we get a newly generated 2-D array (matrix) in which each element of the initial array is repeated along the rows.
NumPy.random()
(i) Numpy.random.randint()
This function returns a list of random integers over a specified interval.
numpy.random.randint(low, high=None, size=None, dtype='l')
→ Low - refers to the start of the interval range.
→ High - refers to the end of the interval range.
→ Size - refers to the no of values to be generated.
→ dtype - refers to the data type of the values generated.
NOTE: if 'high' is not defined, then automatically, samples are generated in the range [0, low). Also, if 'size' is not defined, then only one value is generated.
#numpy.random.randint()
#example 1
list1 = np.random.randint(low= 1, high = 10, size=5, dtype=int)
print(list1)
#example 2
list2= np.random.randint(low=5, size=5)
print(list2)
Output

-> In the first example, we notice that we get five random integers in the range [low=1, high=10).
-> In the second example, we notice that we get five random integers in the range [0, low=5). The range is [0, low=5) since 'high' has not been defined.
(ii) Numpy.random.choice
This function returns a random sample of numbers from an array.
numpy.random.choice(a, size=None, replace=True, p=None)
→ a - refers to the array.
→ Size - refers to no. of samples to be generated or the shape of the output array.
→ Replace - refers to whether the sample is with or without replacement.
→ p - refers to the probability of each sample/element present in the array.
#numpy.random.choice()
arr=[1,2,3,4,5,6,7,8,9,10]
list1 = np.random.choice(arr, 5)
print(list1)
print(len(list1))
Output
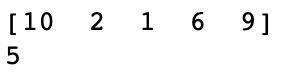
-> In the example, we notice that we get a list of 5 random samples from the array specified.
-> By printing the length of the list, we notice that we get five random samples only.
NumPy.shape
This function returns the shape of the NumPy array specified.
numpy.shape(array_name)
→ array_name - refers to the array specified.
#numpy.shape
arr=[[5,10,15,20,25], [1,2,3,4,5]]
print(np.shape(arr))
Output
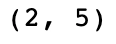
-> In the example, we notice that we get the shape as (2,5). This implies that the 2-D array(matrix) specified has two rows and five columns.
NumPy.min
This function returns the minimum value from the specified array.
numpy.min(array_name)
→ array_name - refers to the array specified.
#numpy.min()
arr=[10,7,1,2,5]
minimum_elem = np.min(arr)
print(minimum_elem)
Output
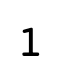
-> In the example, we observe that the output is 1. The number ‘1’ is the minimum element in the array specified.
NumPy.max
This function returns the maximum value from the specified array.
numpy.argmax(array, axis = None, out = None)
#numpy.max()
arr=[10,7,1,2,5]
maximum_elem = np.max(arr)
print(maximum_elem)
Output
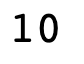
-> In the example, we observe that the output is 10. The number ‘10’ is the maximum element in the array specified.
NumPy.argmax
This function returns the index of the maximum element of the array specified in a particular axis.
numpy.argmax(array, axis = None, out = None)
→ Array - refers to the array specified.
→ Axis - refers to the axis specified. Axis '0' implies along the columns, and axis '1' means along the rows.
→ Out - provides a feature to insert output to the array.
#numpy.argmax()
arr=[[1,2,3,4], [4,1,2,3]]
#max indices along columns
indices_cols = np.argmax(arr, axis=0)
print(indices_cols)
#max indices along rows
indices_rows = np.argmax(arr, axis=1)
print(indices_rows)
Output
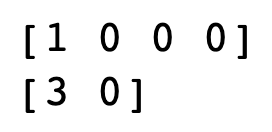
-> In the above example, we have first taken the axis as '0,' i.e., along the columns. We get the result as [1 0 0 0 ]. This is because of the following facts:-
- First column: 1<4, so the max index is 1.
- Second column : 2>1 so max index is 0.
- Third column : 3>1 so max index is 0.
- Fourth column : 4>3 s0 max index is 0.
So, the output is [1 0 0 0].
-> Secondly, we have taken the axis as '1,' i.e., along the rows. We get the result as [3 0]. This is because of the following facts:-
- First row: 1<2<3<4, so the max index is 3.
- Second row : 4>1 ; 4>2 ; 4>3 so max index is 0.
So, the output is [3 0].
NumPy.sort
This function returns a sorted version of the array specified.
numpy.sort(a, axis=- 1, kind=None, order=None)
→ a - refers to the array specified.
→ Axis - refers to the axis specified.
→ Kind – refers to the type of sorting algorithm used.
→ Order - refers to specifying which fields to compare first.
#numpy.sort()
a=np.array([[10,9,8,7,6], [5,4,3,2,1]])
#sorting along the columns with axis=0
arr1= np.sort(a, axis =0, kind=None, order = None )
print(arr1)
print(" ")
#sorting along the rows with axis=1
arr2 = np.sort(a, axis=1, kind=None, order=None)
print(arr2)
Output

-> In the above example, we firstly sort along the columns with axis=’0’. We get the result as displayed above. This is because of the following facts:-
- First column: 10> 5, so we get 5.
- Second column: 9> 4, so we get 4.
- Third column: 8>3, so we get 3.
- Fourth column: 7>2, so we get 2.
- Fifth column: 6>1, so we get 1.
-> Secondly, we sort along the rows with axis=’1’. We get the result as displayed above. This is because of the following facts:-
- First row: 6<7<8<9<10.
- Second row: 1<2<3<4<5.
NumPy.isnan
This function returns a boolean array indicating the presence/absence of NaN values.
numpy.isnan(array)
→ Array - refers to the array specified.
#numpy.isnan()
arr=np.array([1,2,np.nan,3,4])
print(np.isnan(arr))
Output

-> In the example above, we notice that there is only one NaN value in the boolean array.
-> 'True' indicates the presence of the 'NaN' value in the boolean array.
NumPy.mean, Numpy.median, Numpy.std
These functions return the specified list's mean, median, and standard deviation.
numpy.mean()
arr=[1,2,3,4,5]
print(np.mean(arr))
#numpy.median()
print(np.median(arr))
#numpy.std()
print(np.std(arr))
Output

-> In the example above, we notice that we get the mean as 3.0, the median as 3.0, and the standard deviation as 1.41.
NumPy.histogram
This function returns a histogram representing the frequency of data distribution in graphical form.
numpy.histogram(data, bins=10, range=None, normed=None, weights=None, density=None)
→ Data - refers to the array to be plotted.
→ Bins - refers to the number of equal width bars.
→ Range - refers to the lower and upper range of bins.
→ Normed - refers to the density attribute.
→ Weights - refers to the array of weights.
→ Density - refers to an optional parameter relating to probability density function.
#numpy.histogram()
a = np.random.randint(100, size =(50))
#Creating the histogram
np.histogram(a, bins = [0, 10, 20, 30, 40,50, 60, 70, 80, 90, 100])
Output
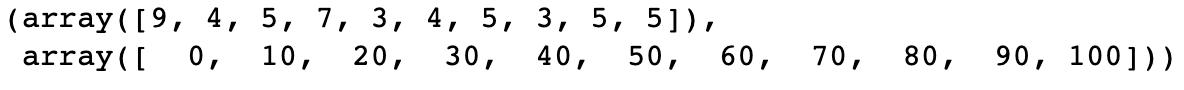
-> In the example above, we notice that two values are returned.
-> The first value refers to the array of values of the histogram.
-> The second value refers to the array of bin edges.
Check out this array problem - Merge 2 Sorted Arrays
Frequently Asked Questions
What is the numpy() method?
The numpy() method doesn't exist directly; instead, NumPy provides a collection of functions, like numpy.array(), for numerical computations and array operations.
What is the most used NumPy function?
The numpy.array() function is the most used, as it creates arrays, the foundation for performing mathematical, statistical, and data manipulation tasks.
What are NumPy commands?
NumPy commands are pre-built functions like numpy.mean(), numpy.sum(), and numpy.reshape() that enable efficient numerical computations and array manipulations in Python.
Conclusion
Congratulations on making it this far. This blog discussed significant NumPy functions for Machine Learning!!
We learned about various numpy function, namely, numpy.linspace, numpy.repeat, numpy.random, numpy.shape, numpy.min, numpy.max, numpy.argmax,
numpy.sort, numpy.isnan, numpy.mean, numpy.median, numpy.std and numpy.histogram.
Recommended Readings:
You can also consider our Machine Learning Course to give your career an edge over others.