Introduction
Linked lists are one of the most essential and often asked data structures in programming contests and technical interviews. There are various standard linked list problems and techniques. This blog tackles a coding task that involves In-place Merge two sorted Linked Lists without changing the links of the first list.
Recommended Topic, Floyds Algorithm and Rabin Karp Algorithm
Problem Statement
You have been given two sorted singly linked lists, each with n and m elements, and you need to merge them utilising constant space. The first n smallest elements in both lists should go into the first list, while the rest should go into the second list. It's important to keep the sorted order. We are not permitted to alter the first linked list's pointers.
Sample Examples
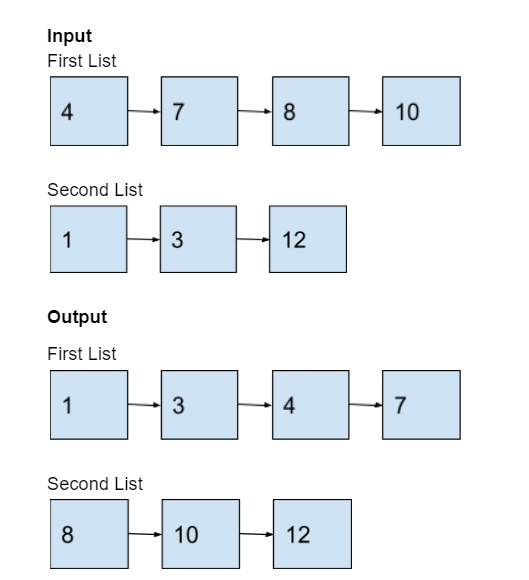
Explanation
The aim is to play around with the next pointers of nodes in the two input lists and arrange them in such a way that all nodes are linked in increasing order of values.
Also read - Merge sort in linked list
In-place Merge Approach
Merge both lists and assign the first m smallest nodes to the first linked list and the remaining n nodes to the second linked list using the merge sort method, where m and n are the total number of items in the first and second linked lists, respectively. But, by changing the links in the first list, this solution violates the problem constraints. However, there is no restriction on swapping data between the linked list nodes.
The concept is to compare each node in the first list to the head node in the second list, swapping data if the current node in the first list is greater than the head node in the second list. With this data exchange, the first list's sorted order will be preserved, while the second list's sorted order may be disturbed. To solve that, use the mergeLists() function to remove the front node from the second list and place it in its proper location in the sorted second list.
Algorithm
-
Make two pointers, let's call them ptr1 and ptr2. Find the smallest of the two nodes by comparing the first node of both lists. Assign pointer ptr1 to the node with the smaller value.
-
Make a pointer to ptr1. Iterating through both lists until the value pointed by ptr1 is less than or equal to the value pointed by ptr2 is what an iteration is all about.
-
Begin iterating and make a variable called temp. In an iteration, it will retain track of the last node in the sorted list.
-
When an iteration is finished, link the temp node to the ptr2 node. ptr1 and ptr2 should be swapped.
- If any of the pointers between ptr1 and ptr2 is NULL, the node referenced by temp should be moved to the next higher value node.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int data;
struct Node *next;
};
void push(struct Node** headref, int newdata)
{
/* allocate the node */
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
new_node->data = newdata;
new_node->next = (*headref);
(*headref) = new_node;
}
// Function to merge two sorted linked lists
void mergeLists(struct Node *l1, struct Node * &l2)
{
while (l1 && l2)
{
// compare elements in l1 with first element in l2
if (l1->data > l2->data)
{
// swap the data
swap(l1->data, l2->data);
struct Node *temp = l2;
//Place the initial element of L2
//in its proper location to keep L2 sorted
if (l2->next && l2->data > l2->next->data)
{
l2 = l2->next;
struct Node *ptr= l2, *prev = NULL;
while (ptr && ptr->data < temp->data)
{
prev = ptr;
ptr = ptr -> next;
}
// update the pointers
prev->next = temp;
temp->next = ptr;
}
}
// move to next element
l1 = l1->next;
}
}
void print(struct Node *head)
{
while (head)
{
cout << head->data << "->" ;
head = head->next;
}
cout << "NULL" << endl;
}
int main()
{
// Creating the two input linked lists.
struct Node *a = NULL;
push(&a, 10);
push(&a, 8);
push(&a, 7);
push(&a, 4);
struct Node *b = NULL;
push(&b, 12);
push(&b, 3);
push(&b, 1);
mergeLists(a, b);
cout << "First List: ";
print(a);
cout << "Second List: ";
print(b);
return 0;
}Implementation in Python
# Structure for a linked list node
class Node:
def __init__(self):
self.data = 0
self.next = None
def push(headref, newdata):
# Allocate node
new_node = Node()
new_node.data = newdata
new_node.next = (headref)
(headref) = new_node
return headref
# Function to merge two sorted linked lists
def mergeLists(l1, l2):
while (l1 and l2):
# compare elements in a with the first element in b
if (l1.data > l2.data):
# Swap the data
l1.data, l2.data = l2.data, l1.data
temp = l2
#Place the initial element of L2
#in its proper location to keep L2 sorted
if (l2.next and l2.data > l2.next.data):
l2 = l2.next
ptr = l2
prev = None
while (ptr and ptr.data < temp.data):
prev = ptr
ptr = ptr.next
# Correct the pointers
prev.next = temp
temp.next = ptr
# Move LL1 pointer to next element
l1 = l1.next
# Function to print the linked link
def printList(head):
while (head):
print(head.data, end = '->')
head = head.next
print('NULL')
# Driver code
if __name__=='__main__':
a = None
a = push(a, 10)
a = push(a, 8)
a = push(a, 7)
a = push(a, 4)
b = None
b = push(b, 12)
b = push(b, 3)
b = push(b, 1)
mergeLists(a, b)
print("First List: ", end = '')
printList(a)
print("Second List: ", end = '')
printList(b)
Output
First List: 1 -> 3 -> 4-> 7-> NULL
Second List: 8 -> 10 -> 12 -> NULLTime Complexity
In the worst-case scenario, we traverse both lists entirely. As a result, O(N+M), where N is the number of nodes in the first list and M is the number of nodes in the second list, remains the same.
Space Complexity
We're utilising the same lists as before, but we've changed the links to make our desired list. As a result, no more room is required. As a result, its spatial complexity is O(1).
Check out this problem - Next Smaller Element




