Introduction
Here in this blog, we are asked to see various approaches to interleave the first half of the queue with the second half. As we are already familiar with the queue data structures. The queue is a linear data structure that has the property of first in first out. That means the element which will first enter the queue will also be the first one to come out. Let's see how we can solve this problem statement. So, let's dig a little deeper into this blog.

Problem Statement
In this problem, we are provided a queue data structure and we are asked to interleave the first half of the queue with the second half. The point to be noted here is that the queue length will always be even. We will see how we will be using the second half of the queue to get this problem solved. Let us understand the problem statement with the help of an example. We need to recall the property of queue data structures i.e. FIFO. the various operations which are performed on queue like enqueue, dequeue, etc need to be kept in mind while approaching the problem.
Sample Examples
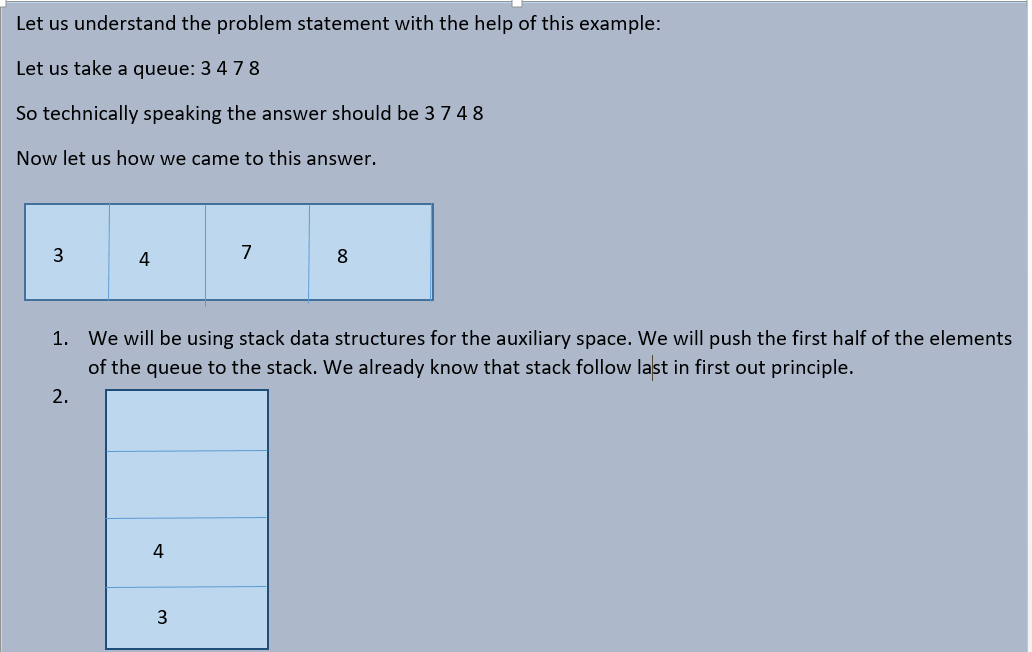


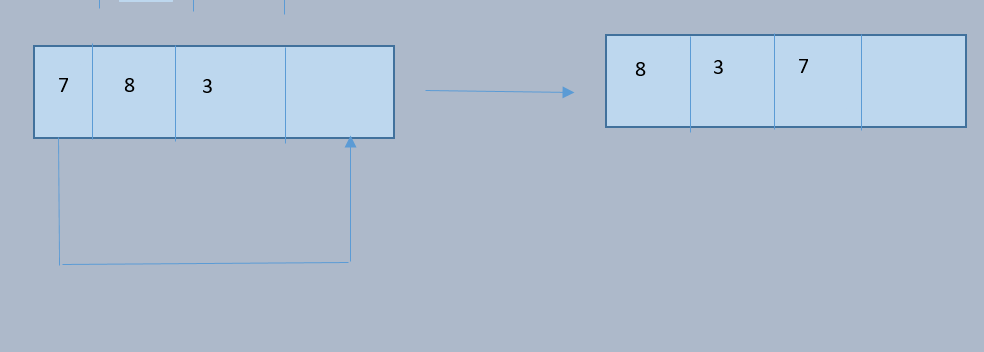

From the above diagram, we can clearly understand the problem statement. We can see how we are interleaving the first half of the queue using the second half.
Brute Force Approach
This approach is very simple to implement and straightforward. We will first push the first half elements of the queue to stack. And after that, we will push back the stack elements. And then delete the first half elements of the queue and enqueue them back. Then again we will push the first half elements into the stack. And as the last step, with the help of the second half, we will Interleave the elements of queue and stack.
Let us see its algorithm.
Steps of Algorithm
Step 1: Enqueue the first half element from the queue to the stack.
Step 2: Remove elements from the stack and enqueue them back to the queue.
Step 3: Move the first half elements of the queue to the end of the queue.
Step 4: Enqueue the first half of the elements to the stack.
Step 5: In interleave fashion, write the elements of the stack to the queue.

Source: brute force approach
Let us see the implementation of this approach in the next section of this blog.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
void inter_Leave_Queue(queue<int>& que)
{
if (que.size() % 2 != 0) // if size is even or not
cout << "Input even number of integers." << endl;
stack<int> s;
int halfSize = que.size() / 2;
for (int i = 0; i < halfSize; i++)
{
s.push(que.front());
que.pop();
}
while (!s.empty())
{ // enqueue back the stack elements
que.push(s.top());
s.pop();
}
for (int i = 0; i < halfSize; i++)
{ // dequeue the first half elements of queue and enqueue them back
que.push(que.front());
que.pop();
}
for (int i = 0; i < halfSize; i++)
{ //Again push the first half elements into the stack
s.push(que.front());
que.pop();
}
while (!s.empty())
{ //interleave the elements of queue and stack
que.push(s.top());
s.pop();
que.push(que.front());
que.pop();
}
}
int main()
{
queue<int> que;
que.push(3);
que.push(4);
que.push(7);
que.push(8); //printing the elements in interleave fashion
cout<<"The elements of the queue in an interleaving fashion are: "<<endl;
inter_Leave_Queue(que);
int length = que.size();
for (int i = 0; i < length; i++)
{
cout << que.front() << " ";
que.pop();
}
return 0;
}
Output:
The elements of the queue in an interleaving fashion are:
3 7 4 8
Implementation in Python
from queue import Queue
def inter_Leave_Queue(que):
if (que.qsize() % 2 != 0): #check if size is even or not
print("Input even number of integers.")
s = []
halfSize = int(que.qsize() / 2)
for i in range(halfSize): #put first half elements into the stack
s.append(que.queue[0])
que.get()
while len(s) != 0: ## enqueue back the stack elements
que.put(s[-1])
s.pop()
for i in range(halfSize): #dequeue the first half elements of queue and enqueue them back
que.put(que.queue[0])
que.get()
for i in range(halfSize): #Again put the first half elements into the stack
s.append(que.queue[0])
que.get()
while len(s) != 0: #interleave function
que.put(s[-1])
s.pop()
que.put(que.queue[0])
que.get()
if __name__ == '__main__':
que = Queue()
que.put(3)
que.put(4)
que.put(7)
que.put(8) #printing the elements in interleave fashion
print("The elements of the queue in an interleaving fashion are: ")
inter_Leave_Queue(que)
length = que.qsize()
for i in range(length):
print(que.queue[0], end = " ")
que.get()
Output:
The elements of the queue in an interleaving fashion are:
3 7 4 8
Let us analyze the time and complexity of this approach.
Complexity analysis
Time complexity
This approach will take O(N) where n is the size of the queue. Because in this approach, the loop is iterating N/2 times and we are using the loops 5 times here in the program. So it will take O(N) time complexity.
Space complexity
And it will take O(N). Since we are using a stack data structure to store it as an auxiliary space.
Read about Application of Queue in Data Structure here.




