Intersection Point in Y shaped Linked Lists

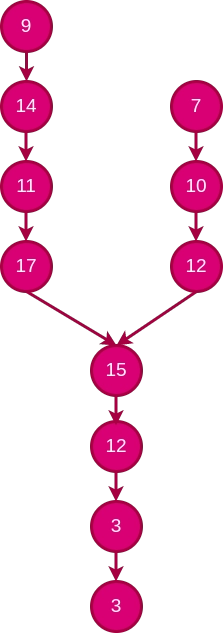
Approach 1 (Brute-Force)

This is a brute force approach. We will run two nested loops. The outer loop will iterate through the first linked list and the inner loop will go over the second linked list. If any node of the second linked list is equal to the current node of the first linked list, output the value of that node. Since the first such node is the intersection point in y shaped linked lists

Algorithm

1. Run two nested loops, L1 and L2. L1 iterates over the nodes of the first linked list and L2 goes over the nodes of the second linked list.

2. Let firstNode be the current node in the outer loop L1.

3. In the current iteration of the inner loop, if any node of the second linked list equals firstNode, output the value of firstNode and return;

4. Repeat Step 3 for each iteration of the outer loop L1.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

class Node
{
public:
    int data;
    Node *next;
};

Node *createNode(int data)
{
    Node *node = new Node();
    node->data = data;
    node->next = NULL;

    return node;
}

Node* findIntersectionNode(Node* head1, Node* head2) {
    Node* ptr1 = head1;
    Node* ptr2 = head2;
    while(ptr1 != NULL) {
        Node* currPtr = ptr2;
        while(currPtr != NULL){
            if(currPtr == ptr1) return currPtr;
            currPtr = currPtr->next;
        }
        ptr1 = ptr1->next;
    }
    return NULL;
}

int main()
{
    Node *newNode;

    // L1 = 9 -> 14 -> 11 -> 17 -> 15 -> 12 -> 3 -> 1
    // L2 = 7 -> 10 -> 12 -> 15 -> 12 -> 3 -> 1
    Node *head1 = createNode(9);

    Node *head2 = createNode(7);

    newNode = createNode(14);
    head1->next = newNode;

    newNode = createNode(11);
    head1->next->next = newNode;

    newNode = createNode(17);
    head1->next->next->next = newNode;

    newNode = createNode(10);
    head2->next = newNode;

    newNode = createNode(12);
    head2->next->next = newNode;

    newNode = createNode(15);
    head1->next->next->next->next = newNode;
    head2->next->next->next = newNode;

    newNode = createNode(12);
    head1->next->next->next->next->next = newNode;
    head2->next->next->next->next = newNode;

    newNode = createNode(3);
    head1->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next = newNode;

    newNode = createNode(1);
    head1->next->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next->next = newNode;

    Node *intersectionNode = findIntersectionNode(head1, head2);
    if (intersectionNode == NULL)
    {
        cout << "No Intersection Point" << endl;
    }
    else
        cout << "Intersection Point: Node with value " << intersectionNode->data << endl;
}

 

Output

Intersection Point: Node with value 15

Time Complexity Analysis

The time complexity of the above algorithm is O(M * N) where M, N are the lengths of first and second linked lists respectively.

It is because we are running two nested for loops over the elements of the given linked lists.

Space Complexity Analysis

The space complexity of the above algorithm is O(1). It is because we are using constant memory in the program.

Read More - Time Complexity of Sorting Algorithms

Approach 2 (Using Hashing)

In this approach, we will traverse the first linked list and store the addresses of each node in a hash such as unordered_map in C++. Now, we will traverse the second linked list and check if any of its node’s address is already hashed. We will output the value of the first such node in the second linked list whose address is already hashed.

Algorithm

1. Iterate over the nodes of the first linked list and hash their addresses using an unordered_map in C++.

2. Now, iterate over the nodes of the second linked list and check if any node is already hashed using the find() function in unordered_map template.

3. Output the value of the first such node in the second linked list. If no such node is found, output - 1.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

class Node
{
public:
    int data;
    Node *next;
};

Node *createNode(int data)
{
    Node *node = new Node();
    node->data = data;
    node->next = NULL;

    return node;
}

int findLength(Node *head1)
{
    int c = 0;
    while (head1 != NULL)
    {
        c++;
        head1 = head1->next;
    }
    return c;
}

Node *findIntersectionNode(Node *head1, Node *head2)
{
    int c1 = findLength(head1);
    int c2 = findLength(head2);
    if (c1 > c2)
        swap(head1, head2);
    unordered_map<Node *, int> hash;

    while (head1 != NULL)
    {
        hash[head1] = 1;
        head1 = head1->next;
    }

    while (head2 != NULL)
    {
        if (hash.find(head2) != hash.end())
        {
            return head2;
        }
        head2 = head2->next;
    }

    return NULL;
}

int main()
{
    Node *newNode;

    // L1 = 9 -> 14 -> 11 -> 17 -> 15 -> 12 -> 3 -> 1
    // L2 = 7 -> 10 -> 12 -> 15 -> 12 -> 3 -> 1
    Node *head1 = createNode(9);

    Node *head2 = createNode(7);

    newNode = createNode(14);
    head1->next = newNode;

    newNode = createNode(11);
    head1->next->next = newNode;

    newNode = createNode(17);
    head1->next->next->next = newNode;

    newNode = createNode(10);
    head2->next = newNode;

    newNode = createNode(12);
    head2->next->next = newNode;

    newNode = createNode(15);
    head1->next->next->next->next = newNode;
    head2->next->next->next = newNode;

    newNode = createNode(12);
    head1->next->next->next->next->next = newNode;
    head2->next->next->next->next = newNode;

    newNode = createNode(3);
    head1->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next = newNode;

    newNode = createNode(1);
    head1->next->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next->next = newNode;

    Node *intersectionNode = findIntersectionNode(head1, head2);
    if (intersectionNode == NULL)
    {
        cout << "No Intersection Point" << endl;
    }
    else
        cout << "Intersection Point: Node with value " << intersectionNode->data << endl;
}

 

Output

Intersection Point: Node with value 15

Time Complexity Analysis

The time complexity of the above approach is O(M + N), where M, N is the number of nodes in the first and second linked lists respectively.

Space Complexity Analysis

The space complexity of the above approach is O(min(M, N)) as we are hashing the addresses of the nodes of the smaller linked list.

Approach 3 (Parallel Traversal)

In this approach we will use a tricky observation based on the count of nodes in both linked lists. Let the distance between the intersection node and head of the smaller linked list be d. Then we will start the iteration of the first linked list from such a node which is at distance d from the intersection node. Now, we will move one node at a time from both linked lists and then output the node where both linked lists point to the same node.

Algorithm

1. Let the number of nodes in L1 and L2 be c1 and c2.

2. Let d = abs(c1 - c2).

3. Move d nodes in the longer linked list.

4. From here onwards, both linked lists have an equal number of nodes to reach the intersection point.

5. Traverse both linked lists parallely, one node at a time and output the value of the first common node.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

class Node
{
public:
    int data;
    Node *next;
};

Node *createNode(int data)
{
    Node *node = new Node();
    node->data = data;
    node->next = NULL;

    return node;
}

int findLength(Node *head1)
{
    int c = 0;
    while (head1 != NULL)
    {
        c++;
        head1 = head1->next;
    }
    return c;
}

Node *findIntersectionNode(Node *head1, Node *head2)
{
    int c1 = findLength(head1);
    int c2 = findLength(head2);
    int d = abs(c1 - c2);

    if (c1 < c2)
    {
        swap(head1, head2);
    }

    while (d > 0)
    {
        head1 = head1->next;
        d--;
    }

    while (head1 != NULL && head2 != NULL)
    {
        if (head1 == head2)
        {
            return head1;
        }
        head1 = head1->next;
        head2 = head2->next;
    }

    return NULL;
}

int main()
{
    Node *newNode;

    // L1 = 9 -> 14 -> 11 -> 17 -> 15 -> 12 -> 3 -> 1
    // L2 = 7 -> 10 -> 12 -> 15 -> 12 -> 3 -> 1
    Node *head1 = createNode(9);

    Node *head2 = createNode(7);

    newNode = createNode(14);
    head1->next = newNode;

    newNode = createNode(11);
    head1->next->next = newNode;

    newNode = createNode(17);
    head1->next->next->next = newNode;

    newNode = createNode(10);
    head2->next = newNode;

    newNode = createNode(12);
    head2->next->next = newNode;

    newNode = createNode(15);
    head1->next->next->next->next = newNode;
    head2->next->next->next = newNode;

    newNode = createNode(12);
    head1->next->next->next->next->next = newNode;
    head2->next->next->next->next = newNode;

    newNode = createNode(3);
    head1->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next = newNode;

    newNode = createNode(1);
    head1->next->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next->next = newNode;

    Node *intersectionNode = findIntersectionNode(head1, head2);
    if (intersectionNode == NULL)
    {
        cout << "No Intersection Point" << endl;
    }
    else
        cout << "Intersection Point: Node with value " << intersectionNode->data << endl;
}

 

Output

Intersection Point: Node with value 15

Time Complexity Analysis

The time complexity of the above approach is O(M + N), where M, N is the number of nodes in the first and second linked lists respectively.

It is because we are running through each node of both linked lists once in the worst case.

Space Complexity Analysis

The space complexity of the above approach is O(1) as we are using constant memory in the program execution.

Approach 4 (Circular Linked List)

This approach is constructive in nature. That is we need to make some constructive changes in the given linked lists to find out the answer. Create a circular linked list in the first one by connecting the first and last nodes. Now, the problem boils down to finding a loop in the second linked list. Have a look at the algorithm to be more clear.

Algorithm

1. Traverse the first linked list and make a circular linked list by connecting the last and first nodes.

2. Now, we know that a loop is created in the second linked list as well due to the above operation.

3. We know the length of the loop in the second linked list. It is equal to the length of the first linked list. Let it be L.

4. Move L nodes in the second linked list from its head. Let the resultant node pointer be ptr1. Now, start traversing the second linked list from its head using a pointer ptr2. Move ptr1 and ptr2 one node at a time. 

5. And when they arrive at a common node, output its value.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

class Node
{
public:
    int data;
    Node *next;
};

Node *createNode(int data)
{
    Node *node = new Node();
    node->data = data;
    node->next = NULL;


    return node;
}

int findLength(Node *head1)
{
    int c = 0;
    while (head1 != NULL)
    {
        c++;
        head1 = head1->next;
    }
    return c;
}

Node *findEndNode(Node *head1)
{
    Node *ptr1 = head1;
    Node *endNode;
    while (ptr1->next != NULL)
    {
        ptr1 = ptr1->next;
    }
    endNode = ptr1;
    return endNode;
}

Node *findIntersectionNode(Node *head1, Node *head2)
{
    int c = findLength(head1);
    Node *ptr1 = head1;

    Node *endNode1 = findEndNode(head1);
    Node *endNode2 = findEndNode(head2);

    if (endNode1 != endNode2)
        return NULL;

    endNode1->next = head1;
    Node *ptr2 = head2;

    int c1 = c;
    while (c1 > 0)
    {
        ptr2 = ptr2->next;
        c1--;
    }
    ptr1 = head2;

    while (ptr1 != NULL && ptr2 != NULL)
    {
        if (ptr1 == ptr2)
            return ptr1;
        ptr1 = ptr1->next;
        ptr2 = ptr2->next;
    }
    return NULL;
}


int main()
{
    Node *newNode;

    // L1 = 9 -> 14 -> 11 -> 17 -> 15 -> 12 -> 3 -> 1
    // L2 = 7 -> 10 -> 12 -> 15 -> 12 -> 3 -> 1
    Node *head1 = createNode(9);

    Node *head2 = createNode(7);

    newNode = createNode(14);
    head1->next = newNode;

    newNode = createNode(11);
    head1->next->next = newNode;

    newNode = createNode(17);
    head1->next->next->next = newNode;

    newNode = createNode(10);
    head2->next = newNode;

    newNode = createNode(12);
    head2->next->next = newNode;

    newNode = createNode(15);
    head1->next->next->next->next = newNode;
    head2->next->next->next = newNode;

    newNode = createNode(12);
    head1->next->next->next->next->next = newNode;
    head2->next->next->next->next = newNode;

    newNode = createNode(3);
    head1->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next = newNode;

    newNode = createNode(1);
    head1->next->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next->next = newNode;

    Node *intersectionNode = findIntersectionNode(head1, head2);
    if (intersectionNode == NULL)
    {
        cout << "No Intersection Point" << endl;
    }
    else
        cout << "Intersection Point: Node with value " << intersectionNode->data << endl;
}

 

Output

Intersection Point: Node with value 15

Time Complexity Analysis

The time complexity of the above algorithm is O(M + N) where M, N is the number of nodes in both the linked lists respectively.

Space Complexity Analysis

The space complexity of the above approach is O(1) as we are using constant memory in the program execution.

Approach 5 (Mathematical Approach)

In this approach we will make use of modifying the first linked list and a few mathematical equations to find the answer. Let us see the detailed solution in the Algorithm section given below.

Algorithm

1. Let C1, C2 be the length of first and second linked lists respectively.

2. Let X be the length of the first linked list until the intersection point in y shaped linked lists occurs.

3. Similarly, let Y be the length of the second linked list until the intersection point.

4. Let Z be the length of the linked list from the intersection point to the end of any linked list including the intersection node. Now, we have the following equations:

X + Z = C1
Y + Z = C2

5. Reverse the first linked list.

6. Traverse the second linked list. Let C3 be the length of the second linked list - 1. Now, we have the following equation:

X + Y = C3

7. As you can observe, we have 3 equations and three unknowns and hence, the variables X, Y, Z are solvable.

X = (C1 + C3 – C2)/2;
Y = (C2 + C3 – C1)/2;
Z = (C1 + C2 – C3)/2;

8. Find the value of X and traverse that many nodes in the first linked list.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

class Node
{
public:
    int data;
    Node *next;
};

Node *createNode(int data)
{
    Node *node = new Node();
    node->data = data;
    node->next = NULL;

    return node;
}

int findLength(Node *head1)
{
    int c = 0;
    while (head1 != NULL)
    {
        c++;
        head1 = head1->next;
    }
    return c;
}

Node *reverseList(Node *head)
{
    Node *current = head;
    Node *prev = NULL, *next = NULL;

    while (current != NULL)
    {
        next = current->next;
        current->next = prev;

        prev = current;
        current = next;
    }
    head = prev;
    return head;
}


Node *findIntersectionNode(Node *head1, Node *head2)
{
    int C1 = findLength(head1);
    int C2 = findLength(head2);

    head1 = reverseList(head1);

    int C3 = findLength(head2);

    int X = (C1 + C2 - C3) / 2;
    while (X > 0)
    {
        X--;
        head1 = head1->next;
    }
    return head1;
}


int main()
{
    Node *newNode;

    // L1 = 9 -> 14 -> 11 -> 17 -> 15 -> 12 -> 3 -> 1
    // L2 = 7 -> 10 -> 12 -> 15 -> 12 -> 3 -> 1
    Node *head1 = createNode(9);

    Node *head2 = createNode(7);

    newNode = createNode(14);
    head1->next = newNode;

    newNode = createNode(11);
    head1->next->next = newNode;

    newNode = createNode(17);
    head1->next->next->next = newNode;

    newNode = createNode(10);
    head2->next = newNode;

    newNode = createNode(12);
    head2->next->next = newNode;

    newNode = createNode(15);
    head1->next->next->next->next = newNode;
    head2->next->next->next = newNode;

    newNode = createNode(12);
    head1->next->next->next->next->next = newNode;
    head2->next->next->next->next = newNode;

    newNode = createNode(3);
    head1->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next = newNode;

    newNode = createNode(1);
    head1->next->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next->next = newNode;

    Node *intersectionNode = findIntersectionNode(head1, head2);
    if (intersectionNode == NULL)
    {
        cout << "No Intersection Point" << endl;
    }
    else
        cout << "Intersection Point: Node with value " << intersectionNode->data << endl;
}

 

Output

Intersection Point: Node with value 15

Time Complexity Analysis

The time complexity of the above algorithm is O(M + N) where M, N is the number of nodes in the first and second linked list respectively.

It is because we are iterating over the nodes of the two linked lists a finite number of times.

Space Complexity Analysis

The space complexity of the above algorithm is O(1) as we are using constant memory in the program execution.

Approach 6

Let us do a calculation to understand this approach. Count the number of nodes traversed in each of the following two traversals:

T1: Traverse the first linked list and when the end node is encountered, traverse the second list up to the intersection point.

T2: Traverse the second linked list and when the end node is encountered, traverse the first linked list up to the intersection point.

You will find that the same number of nodes are traversed in each of the above-mentioned traversals. Now, let us see the algorithm.

Algorithm

1. Traverse both linked lists parallel to each other one node at a time.

2. When the end node is encountered in any traversal, traverse through the head of the other linked list.

3. When a common node is encountered, output its value.

4. If no common node is encountered after the second traversal, output -1.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

class Node
{
public:
    int data;
    Node *next;
};

Node *createNode(int data)
{
    Node *node = new Node();
    node->data = data;
    node->next = NULL;

    return node;
}

Node *findIntersectionNode(Node *head1, Node *head2)
{
    Node *ptr1 = head1, *ptr2 = head2;
    int reassign = 0;
    while (true)
    {
        if (ptr1 == NULL)
        {
            if (reassign == 1)
            {
                return NULL;
            }
            reassign = 1;
            ptr1 = head2;
        }
        if (ptr2 == NULL)
        {
            ptr2 = head1;
        }
        if (ptr1 == ptr2)
        {
            return ptr1;
        }
        ptr1 = ptr1->next;
        ptr2 = ptr2->next;
    }
    return NULL;
}

int main()
{
    Node *newNode;


    // L1 = 9 -> 14 -> 11 -> 17 -> 15 -> 12 -> 3 -> 1
    // L2 = 7 -> 10 -> 12 -> 15 -> 12 -> 3 -> 1
    Node *head1 = createNode(9);

    Node *head2 = createNode(7);

    newNode = createNode(14);
    head1->next = newNode;

    newNode = createNode(11);
    head1->next->next = newNode;

    newNode = createNode(17);
    head1->next->next->next = newNode;

    newNode = createNode(10);
    head2->next = newNode;

    newNode = createNode(12);
    head2->next->next = newNode;

    newNode = createNode(15);
    head1->next->next->next->next = newNode;
    head2->next->next->next = newNode;

    newNode = createNode(12);
    head1->next->next->next->next->next = newNode;
    head2->next->next->next->next = newNode;

    newNode = createNode(3);
    head1->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next = newNode;

    newNode = createNode(1);
    head1->next->next->next->next->next->next->next = newNode;
    head2->next->next->next->next->next->next = newNode;

    Node *intersectionNode = findIntersectionNode(head1, head2);
    if (intersectionNode == NULL)
    {
        cout << "No Intersection Point" << endl;
    }
    else
        cout << "Intersection Point: Node with value " << intersectionNode->data << endl;
}

 

Output

Intersection Point: Node with value 15

Time Complexity Analysis

The time complexity of the above algorithm is O(M + N) where M, N is the number of nodes in the first and second linked list respectively.

It is because we are iterating over the nodes of the two linked lists a finite number of times.

Space Complexity Analysis

The space complexity of the above algorithm is O(1) as we are using constant memory in the program execution.

Frequently Asked Questions

Can you devise a simple algorithm to find if the input linked lists are intersecting or not?

Just check if the end nodes of the input linked lists are the same or not.

Which data structure is faster for traversal - Arrays or Linked Lists?

Arrays are faster in traversal. Operations such as accessing a specific element, traversal, etc. are faster in case of Arrays.

Why are arrays better than linked lists?

Arrays provide random access and need less memory per element (no pointer space is required), but they are inefficient for insertion/deletion operations and memory allocation. Linked lists, on the other hand, are dynamic and have lower insertion/deletion time complexity.

Conclusion

This blog discussed the problem of finding the intersection point in y shaped linked lists in great detail with numerous approaches. We studied various trickier observations to find the intersection point in y shaped linked lists. We also made structural changes in the linked lists to obtain the solution in some approaches. 

Hope you liked the article. Please follow the below mentioned articles on DSA problems to practice more on this topic.

LCA of three nodes, Sum of Infinite Array, Reverse Nodes in k-Group, Add two numbers in Linked Lists, Merge Two Sorted Lists, Implement a Queue, Flattening A Linked List.