Introduction to Sparse Matrix

Introduction

Let's ensure we understand the foundational concepts before delving further into the subjects. Here is a brief introduction if you are unfamiliar with the Matrix.

A two-dimensional array with "m" rows and "n" columns is known as a matrix. A matrix with m rows and n columns is known as the m × n matrix. It consists of a collection of numbers arranged in either horizontal or vertical rows of entries

In this blog, we will discuss a Sparse Matrix in which we have explained The sparse Matrix class, Filling a Sparse matrix, and supported operators and functions.

Without further ado, let's get started.

Sparse Matrix

A sparse Matrix is a matrix with huge numbers of entries with a value of zero. In other words, the Sparse Matrix is a matrix with very few nonzero elements.

Advantages of the sparse Matrix:

Storage: Given that a sparse matrix has fewer nonzero elements than zero, its elements can be stored in less memory. It only assesses the elements that are not zero.

Computing time: When searching in a sparse matrix, we should only explore the nonzero entries rather than the entire sparse Matrix. Computation time is reduced by logically creating a data structure that traverses nonzero components.

The SparseMatrix class

The primary representation of a sparse matrix in Eigen's sparse module is the class SparseMatrix, which boasts fast performance and little memory usage. It carries out a more flexible version of the common Compressed Column (or Row) Storage method.

💁 It includes four  small arrays:

• Values: keeps track of the nonzero coefficient values.
   
• InnerIndices: keeps track of the nonzero row (or column) indices.
   
• OuterStarts: saves the index of the first nonzero in the previous two arrays for each column (or row).
   
• InnerNNZs: the number of nonzero values for each column is stored (resp. row). The term "inner" defines an inner vector that is either a row for a matrix with a row-major or a column for a matrix with a column major. The word outer indicates the opposite direction.
   

Here is an example that will help to further explain this storage system.

Column major representation:

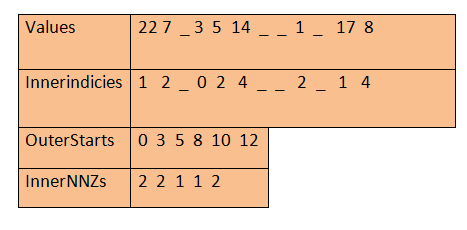
The elements of the given vector are always sorted by increasing inner indices. The ‘_’ represents available free space to insert new elements.

Suppose the case where no free space is available is a compressed mode. It is comparable to the widely used Compressed Column (or Row) Storage methods (CCS or CRS). Using the SparseMatrix::makeCompressed() function, any SparseMatrix can be converted to this format. Given that we have the equivalence, we can say that the InnerNNZs array is redundant with the OuterStarts array in this situation: InnerNNZs[j] == OuterStarts[j+1] - OuterStarts[j]. Therefore, in actual usage, a call to SparseMatrix::makeCompressed() releases this buffer.

Compressed sparse matrices are the end product of all Eigen processes. On the other hand, adding a new element causes a SparseMatrix to switch from the compressed mode to the uncompressed mode later.

Here is the previous Matrix in compressed mode.

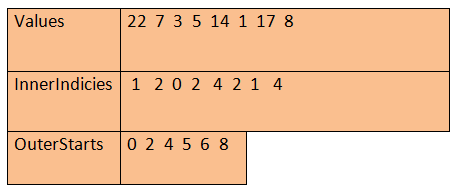
A Sparse vector is also a sparse matrix where values and inner indices are stored. There is no concept of compressed and uncompressed modes.

Matrix and vector properties

The scalar type, the sparse Matrix, and the sparse vector classes each require three template arguments (e.g., double), the inner index type, and the storage order (ColMajor or RowMajor; ColMajor is the default) (default is int).

Constructors use the object's size when creating dense matrix objects. Here are a few instances:

SparseMatrix<std::complex<float> > matrix(1000,2000);
SparseMatrix<double,RowMajor> matrix(1000,2000);
SparseVector<std::complex<float> > vector(1000);              
SparseVector<double,RowMajor> vector(1000);                   

 

Iterating over the nonzero coefficients

The coeffRef(i,j) function provides random access to the components of a sparse object. However, this function necessitates a somewhat costly binary search. Most of the time, one simply wishes to repeat iterations over nonzero elements. This is accomplished using a regular loop over the outer dimension followed by an InnerIterator iterating through the nonzero elements of the current inner vector. To visit the nonzero items, one must do so in the same order as the storage order. 

Here is an example:

SparseMatrix<double> matrix(rows,cols);
for (int m=0; m<matrix.outerSize(); ++m)
 for (SparseMatrix<double>::InnerIterator i(matrix,m); i; ++i)
 {
   i.value();
   i.row();   // It is for row index
   i.col();   // It is for column index 
   i.index(); // It is for inner index
 }

The valueRef() function allows the referenced value for a writable expression to be changed.

Filling a sparse matrix

💁 It is important to take extra precautions when adding new nonzero entries because of the SparseMatrix's unique storage design. One pure random insertion, for instance, into a SparseMatrix would cost O(nnz), where nnz is the number of non-zero coefficients now present.

Thus, building a list of so-called triplets first, then converting it to a SparseMatrix, is the quickest way to produce a sparse matrix while still ensuring decent performance.

Here's an example of how it's usually used:

typedef Eigen::Triplet<double> T;
std::vector<T> tripletList;
tripletList.reserve(estimation_of_entries);
for(...)
{
 // ...
 tripletList.push_back(T(i,j,v_ij));
}
SparseMatrixType matrix(rows,cols);
matrix.setFromTriplets(tripletList.begin(), tripletList.end());
// matrix is ready.

 

However, in rare circumstances, directly entering the nonzeroes into the destination matrix can result in improved performance and reduced memory usage. Below is an example of a typical case using this method:

1: SparseMatrix<double> matrix(rows,cols);         
2: matrix.reserve(VectorXi::Constant(cols,6));
3: for each m,n such that v_mn != 0
4: matrix.insert(i,j) = v_mn;                    
5: matrix.makeCompressed();                                        

Supported operators and functions

💁 Sparse matrices cannot provide the same degree of flexibility as dense matrices due to their unique storage style. Only the portion of the dense matrix API that can be effectively implemented was chosen to be exposed in Eigen's sparse module. The terms "sparse matrix," "sparse vector," "dense matrix," and "dense vector" are used in the following.

Basic operations

Sparse expressions allow most of the unary and binary coefficient wise operations:

sm1.real()    sm1.imag()    -sm1                    0.5*sm1
sm1+sm2      sm1-sm2      sm1.cwiseProduct(sm2)

 

The storage orders need to match, though, which is a significant restriction. Consider the example that follows:

sm4 = sm1 + sm2 + sm3;

 

Binary coefficient wise operators

sm2 = sm1.cwiseProduct(dm1);
dm2 = sm1 + dm1;
dm2 = dm1 - sm1; 

 

Performance-wise, two steps are preferable for adding or subtracting sparse and dense matrices. Rather than writing dm2 = sm1 + dm1, for example, write:

dm2 = dm1;
dm2 += sm1;

 

This variant has the benefit of fully utilising the faster performance of dense storage (no indirection, SIMD, etc.) and paying the price of sluggish sparse evaluation on the sparse matrix's few nonzero elements only.

Also supported by transposition are sparse expressions:

sm1 = sm2.transpose();
sm1 = sm2.adjoint();

Matrix Products

📜 Following is a list of the different types of sparse matrix products that Eigen supports:

Sparse-dense.

dv2 = sm1 * dv1;
dm2 = dm1 * sm1.adjoint();
dm2 = 2. * sm1 * dm1;

 

Symmetric sparse-dense.

dm2 = sm1.selfadjointView<>() * dm1;          
dm2 = sm1.selfadjointView<Upper>() * dm1;     
dm2 = sm1.selfadjointView<Lower>() * dm1;

Sparse-sparse.

sm3 = sm1 * sm2;
sm3 = 4 * sm1.adjoint() * sm2;

Permutations.

PermutationMatrix<Dynamic,Dynamic> P = ...;
sm2 = P * sm1;
sm2 = sm1 * P.inverse();
sm2 = sm1.transpose() * P;

dv2 = sm1 * dv1;
dm2 = dm1 * sm1.adjoint();
dm2 = 2. * sm1 * dm1;

 

Block operations

📜 For read access to sub-matrices, such as blocks, columns, and rows, sparse matrices expose the same API as dense matrices. For a thorough introduction, see Block operations. On the other hand, writing to a sub-sparse matrix is significantly more constrained due to performance issues, and only contiguous groups of columns (or rows) of a column-major (or row-major) SparseMatrix are currently writable. Additionally, block(...) and corner* methods must not be used because this information must be known at compile-time (...). Below is a list of the APIs that can be used to write to a sparse matrix:

SparseMatrix<double,ColMajor> sm1;
sm1.col(j) = ...;
sm1.leftCols(ncols) = ...;
sm1.middleCols(j,ncols) = ...;
sm1.rightCols(ncols) = ...;
SparseMatrix<double,RowMajor> sm2;
sm2.row(i) = ...;
sm2.topRows(nrows) = ...;
sm2.middleRows(i,nrows) = ...;
sm2.bottomRows(nrows) = ...;

Triangular and self adjoint views

📜 In the same way, as with dense matrices, the triangularView() method can be used to address a triangle portion of the Matrix and carry out triangular solves with a dense right-hand side:

dm2 = sm1.triangularView<Lower>(dm1);
dv2 = sm1.transpose().triangularView<Upper>(dv1);

 

The selfadjointView() method allows for a number of operations:

Improved sparse-dense matrix products.

dm2 = sm1.selfadjointView<>() * dm1;         
dm2 = sm1.selfadjointView<Upper>() * dm1;     
dm2 = sm1.selfadjointView<Lower>() * dm1;    

Copy of triangular parts:

sm2 = sm1.selfadjointView<Upper>();                               
sm2.selfadjointView<Lower>() = sm1.selfadjointView<Upper>();      

Use of symmetric permutation:

PermutationMatrix<Dynamic,Dynamic> P = ...;
sm2 = A.selfadjointView<Upper>().twistedBy(P);                                
sm2.selfadjointView<Lower>() = A.selfadjointView<Lower>().twistedBy(P);