Introduction
Postorder Traversal is just traversing the tree to visit all of its descendant nodes before the root node in Depth First Search Fashion. It also implies that the ROOT node of the binary tree must be visited at last.
The order in which postorder traversal follows is:
LeftSubtree -> RightSubtree -> Root
Let’s take an expression:
A + B, assume “+” as a root, A, and B as the left and right children of the tree.
Now, if we need to visit or traverse the expression in a postorder sequence, the resultant expression will be = AB+
This is one of the applications of Postorder traversal to find the postfix expression of a given expression.
Now, consider the below example:
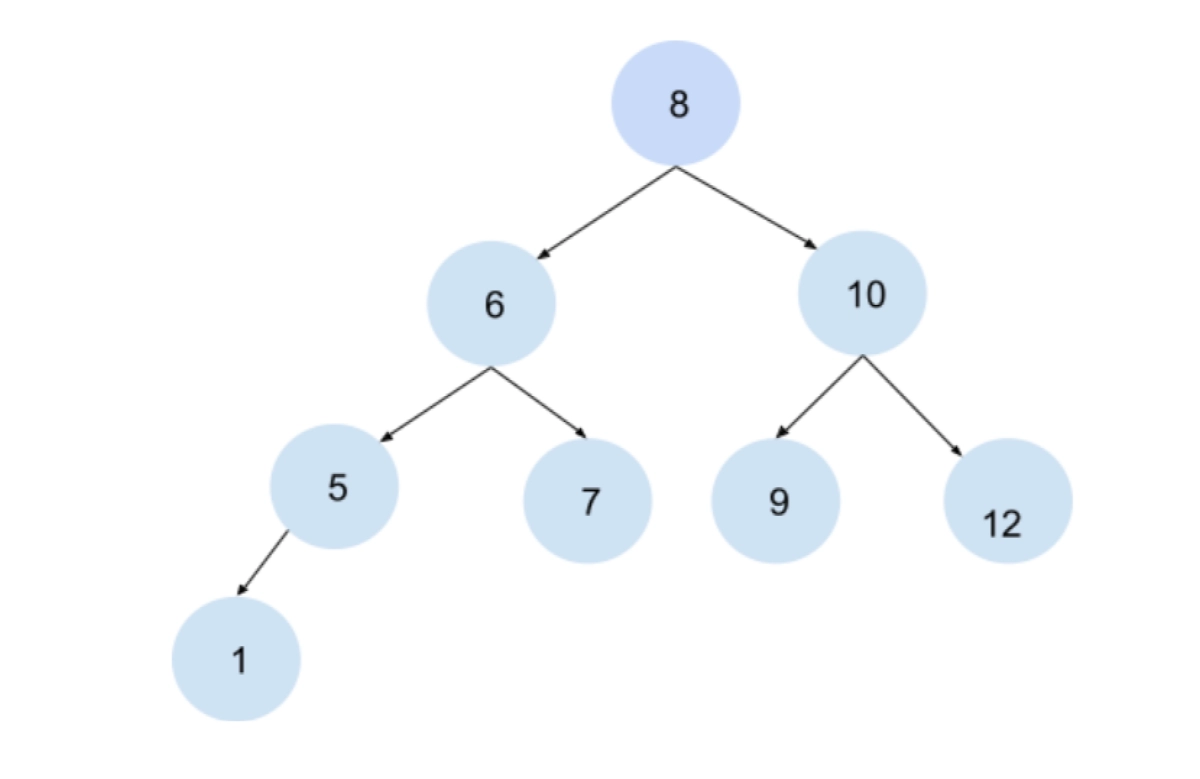
Postorder Traversal:- 1 5 7 6 9 12 10 8
How does it work?
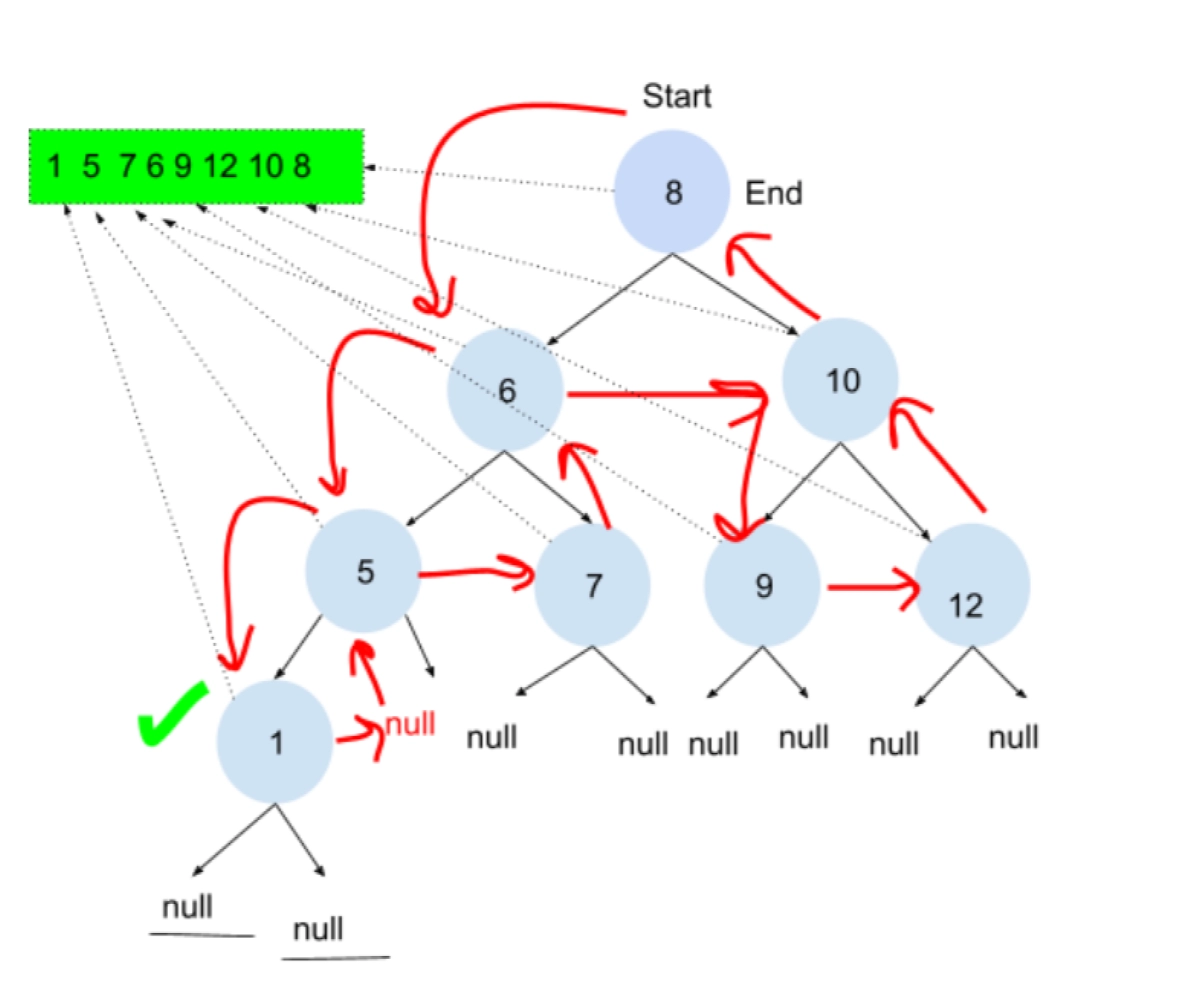
We begin by traversing the nodes in such a way that the leftmost node is visited first. Afterward, we go to its sibling if it exists, i.e., the right node. If the right node is not a leaf node, then we again look for its leftmost node. As you can see in the above example, 1 is the leftmost node since it has no sibling; thus, it moves to its parent node 5. Now, the parent node is also a child of some other node. The pointer will directly point to its sibling node,i.e., 7. Since 7 is the leaf node, the pointer moves to its parent node 6.
The same procedure will occur in the rest of the nodes, as seen in the above representation. We’ll require an additional data structure for tracking the nodes, i.e., a stack that follows LIFO( Last-in-first-out).
Now, let’s get started with the approach:
Recommended: Try the Problem yourself before moving on to the solution
Method - Using Single stack
The idea is to push the nodes onto the stack until we encounter the leftmost node, then move to its sibling node if it exists; if the right node is a leaf node, then print whoever node is at the top of the stack. Else move to its children and apply the same procedure.
Following is the detailed algorithm:
Algorithm:
Step1:- Create an empty stack.
Step2:- Create a variable current that will initialize with root.
current = root
Step 3:- Run a while loop until the stack becomes empty or the current points to null.
Step 3.1:- Begin traversing the tree and pushing the nodes onto the stack by incrementing the current variable to the next left node until it hits null.
current = current->left;
Step 3.2:- When the current variable is null, create a previousNode variable of type Node that points to the right child of the node at the top of the stack.
Node previousNode = stack.top()->right
Step 3.3:- If the previousNode is null, pop the peek value from the stack and assign it to the previousNode. Now, Print previousNode.
Step 3.4:- Run a while loop until the stack becomes and the value in the previousNode matches the right node of the node present at the top of the stack.
Step 3.4.1:- Pop the top value from the stack and assign the popped value to the previousNode.
Step 3.4.2:- Print previousNode.
Step 3.5:- If the previousNode isn’t null, assign its value to the current Node.
Continue following the above steps until the stack becomes empty.
Refer to the below Pseudo Code and try to dry run the Implementation for better understanding:-
Pseudo Code
Create an empty stack
Node current = root
while(current != null or !stack.isEmpty())
if(current != null)
stack.push(current)
current = current->left
else
Node previousNode = stack.top().right
if(previousNode == null)
previousNode = stack.top()
stack.pop()
print(previousNode)
while(!stack.isEmpty() and previousNode == stack.top().right)
previousNode = stack.top()
stack.pop()
print(previousNode)
else
current = previousNode
Consider the below example:
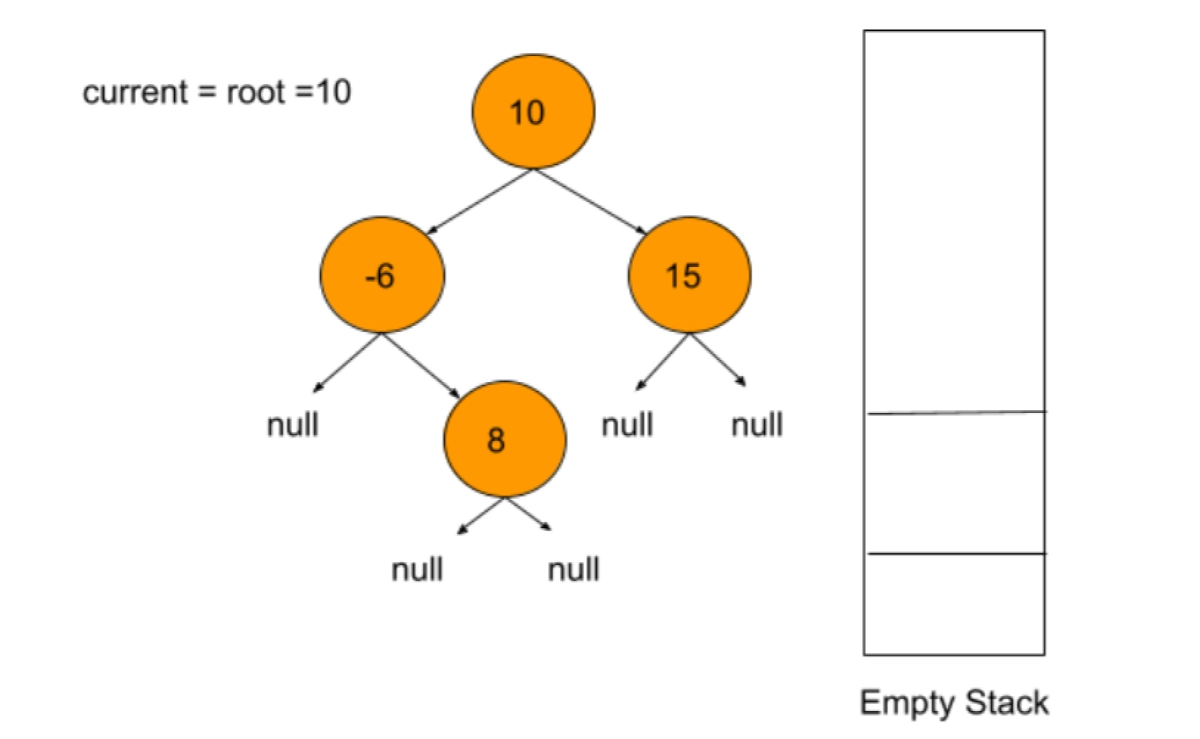
We keep on pushing the left nodes onto the stack until the current hits the null, as shown below:
if(current != null)
stack.push(current)
current = current->left
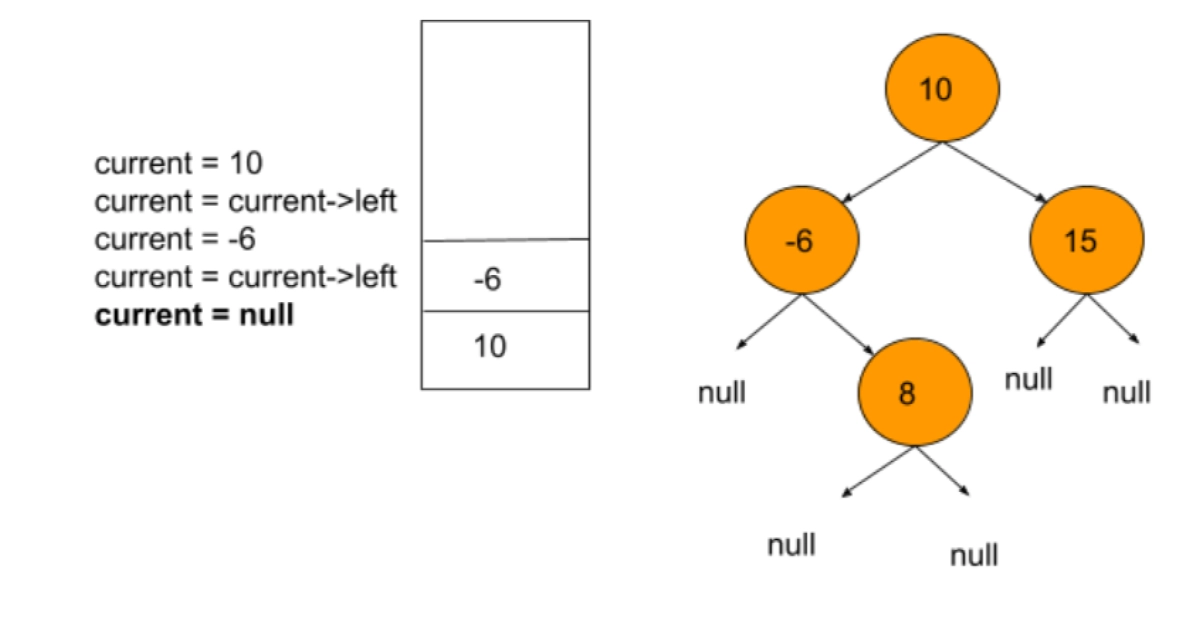
Now that the current is null, but the stack isn't empty, we can proceed to the else part, which involves the previousNode variable.
else
Node previousNode = stack.top().right
The previousNode is assigned as the right child of the node at the top of the stack, i.e., -6->rightchild = 8.
Therefore, previousNode = 8
Since previousNode is not null, the value existing in previousNode will be assigned to the current.
else
current = previousNode

Because the current is no longer null, the value at current will be pushed onto the stack once again.
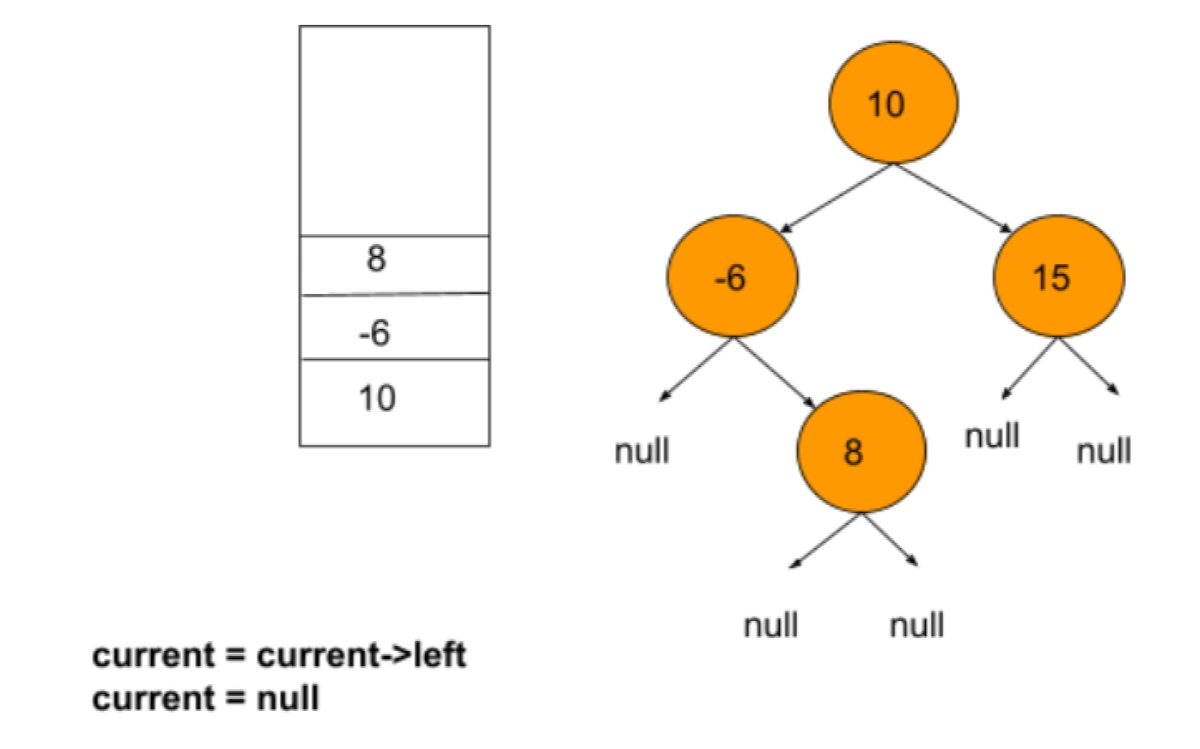
Because the current is now null, the else section will be executed, and the previousNode variable will be set to a different value if it exists.
Node 8 is at the top of the stack, and because it is a leaf node, the previousNode will now refer to null, indicating that there are no further nodes to visit. The top element of the stack will be popped out, and its value will be assigned to the previousNode.
Finally, print the previousNode.
if(previousNode == null)
previousNode = stack.top()
stack.pop()
print(previousNode)
The while loop will then run until the right child of the node at the top of the stack has the same value as the previousNode, and the stack isn’t empty.
while(!stack.isEmpty() and previousNode == stack.top().right)
previousNode = stack.top()
stack.pop()
print(previousNode)
Inside the loop, the previousNode will be updated with the value at the top of the stack, and finally, the value of previousNode gets printed.
The inner while loop will terminate if any one of the conditions fails. Because
previousNode = -6, which is not equal to 8, the loop will terminate.
The same procedure will be carried out for the rest of the nodes.
The final output will be:-
8 -6 15 10
It’s a bit complex to understand this approach, but you’ll find it very easy once you grab the idea.
Now, let’s look at the Implementation for the same:-
Implementation in Java
// Java program for postorder traversal of a binary tree using one stack
import java.io.*;
import java.util.*;
// A binary tree node with three components data , leftChild, and rightChild
class Node
{
int data;
Node left, right;
Node(int value)
{
data = value;
left = right;
}
}
public class PostOrderTraversal {
Node root;
// An iterative function to do postorder traversal
// of a given binary tree
public void postOrderItrOneStack(Node root){
// Initialize current with root
Node current = root;
// Create an empty stack
Stack<Node> stack = new Stack<>();
// Run the while until the stack becomes empty or the current becomes null
while(current != null || !stack.isEmpty()){
// Push the left nodes onto the stack until the current becomes null
if(current != null){
stack.push(current);
// Move the current to the next left node
current = current.left;
// When current is null, move to the else section
}else{
// Initialze a new node with the rightChild of the node present at the top of the stack
Node previousNode = stack.peek().right;
// If no rightChild found pop out the node from the stack and print it
if (previousNode == null) {
previousNode = stack.pop();
System.out.print(previousNode.data + " ");
// Run a while loop until the previousNode matches with the rightChild of the node present at the top of the stack
while (!stack.isEmpty() && previousNode == stack.peek().right) {
// Pop the node and print it
previousNode = stack.pop();
System.out.print(previousNode.data + " ");
}
}
// If right child Found assign the value of previousNode to the current Node and repeat the process until the stack becomes empty
else {
current = previousNode;
}
}
}
}
public static void main(String args[]){
PostOrderTraversal tree = new PostOrderTraversal();
// Construct the below tree
/*
10
/ \
-6 15
\
8
*/
tree.root = new Node(10);
tree.root.left = new Node(-6);
tree.root.right = new Node(15);
tree.root.left.right = new Node(8);
System.out.println("Postorder traversal of a binary tree is :");
// Function calling
tree.postOrderItrOneStack(tree.root);
}
}
Output
Postorder traversal of a binary tree is :
8 -6 15 10
Complexity Analysis
Time Complexity:- The time complexity is O(n), where n is the total number of nodes. Since every node is visited once, therefore, the complexity comes as O(n).
Space Complexity:- The Space Complexity is O(h), where h is the height of the tree. The complexity of the skewed binary tree can reach up to O(n), where n is the number of nodes.
Check out this problem - Mirror A Binary Tree





