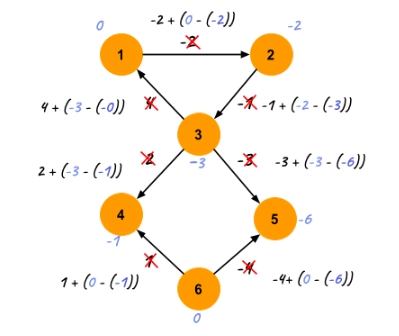
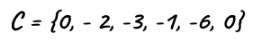Problem Statement
You are given a weighted directed graph having N vertices and M edges. You have to find the shortest distance between every pair of vertices. The weight of the edges in the graph can be negative.
Approach
For a vertex, we can find the shortest distance to all the other vertices in the given graph using the Dijkstra algorithm with minimum priority queue in O(V + E log V) time complexity. Applying the algorithm for every vertex in the graph, we can find the shortest distance between all the pairs in O(V^2 + VE log V) time complexity.
The problem with the Dijkstra algorithm is that we can't apply it to the graphs having a negative weight edge.
The idea of Johnson's algorithm is that if we can transform the given graph to a graph so that all the edge weights are positive, we can apply the Dijkstra Algorithm.
Can we add the minimum weight edge to all the edges??
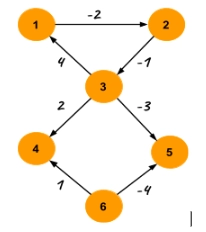
The most straightforward approach to make all the edge weights positive is to add the minimum weight edge to all the edges. But the problem with this approach is that the shortest path may not remain the shortest after adding the minimum weight edge to all the vertices. See the example below for a better understanding -
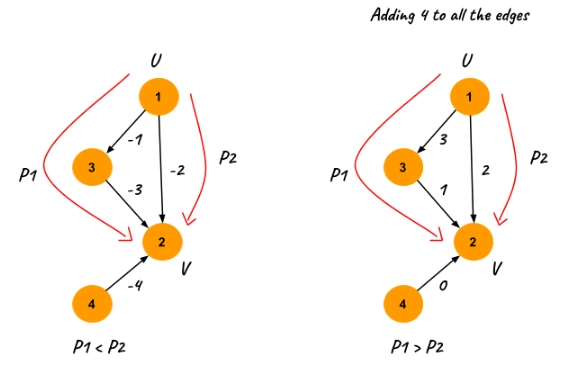
In the example p1 and p2 are two distinct paths between node 1 and 2 and initially p1 < p2. But after adding 4 (absolute value of minimum weight) to all the edges p2 < p1.
So we have to increment each edge weight in such a way that all the edge weights become positive, and all the paths between every pair of vertices increased by the same amount so that the shortest path doesn't change.
Johnson's algorithm achieves that by assigning each vertex an integer. Let there be two vertices, u and v, such that there is an edge (u -> v) between them. If C[u] and C[v] are the integers assigned to u and v, respectively, then the algorithm increases the edge weight by (C[u] - C[v]).
Why does this works??
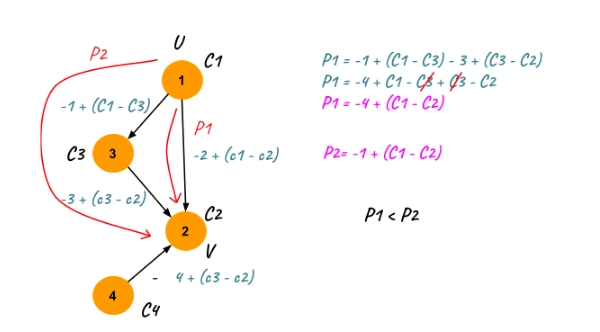
As shown in the example above, for two vertices u and v, all the path lengths will increase by C[u] -C[v], and all the other values of C[] get canceled out.
How to calculate the values of C[]??
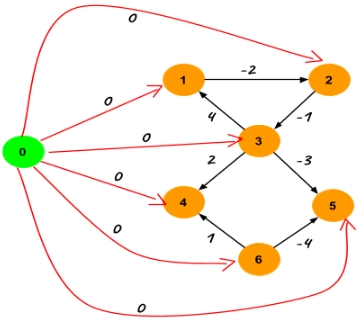
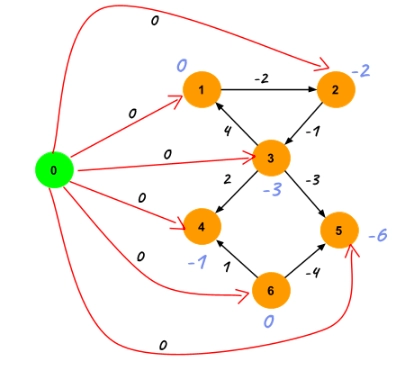
To calculate the value C[] for each vertex, add a new vertex in the graph and connect it to all the other vertices by the edges of weight zero directed from the new vertex to the existing vertex. This does not change the shortest path between any pair.
Now, use the Bellman-Ford algorithm to find the shortest distance to every vertex from the new vertex. The shortest distance values are values of c[].