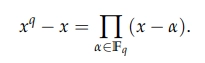Index Calculus
- Index calculus is a technique for calculating discrete logarithms in a finite field's multiplicative group.
- Number theory and cryptography research on index calculus is extensive. A sizable family of algorithms with numerous applications utilizes this method.
- These algorithms can factor big integers, compute discrete logarithms in finite fields, determine the class numbers of a number field, and even compute discrete logarithms on particular algebraic curves' Jacobians.
- The applications mentioned above are intriguing from a cryptographic point of view. However, index calculus approaches have also recently been employed in some specific settings to compromise the security of many cryptographic primitives.
Now that we know a little about discrete logarithm problems and Index calculus, we are good to go with Joux’s Index Calculus for fields of small characteristics.
Joux’s Index Calculus for Fields of Small Characteristic
This section will discuss Joux’s approach to solve the Discrete Logarithm problem, explained above, and then will explore the difference between Joux’s algorithm and the traditional Index Calculus Algorithm.
Joux’s Approach
Joux’s index calculus for fields of small characteristics to solve discrete logarithm in (F2n *,.) undertakes an approach that relies on the observation that, if 2n = (q 2 ) k, then F2n can be seen as a degree k extension of Fq2.
We have something important to keep in mind, that is, for this algorithm to work effectively, we require k to be roughly the similar size of q; if n does not contain a desirable factor k, then we have to work in a minor extension of F2n whose degree can be factored in the way that is required.
Joux index calculus approach takes all polynomials over Fq2 as a factor base with a degree at most 2. The elements of F2n = F(q2)k are considered polynomials over Fq2.
Difference from Traditional Index Calculus Algorithm
Joux’s Index Calculus algorithm differs from the traditional Index Calculus algorithm in the procedure to obtain the relations among the elements of the factor base. Unlike the traditional approach of taking random polynomials and testing them to find whether they can be expressed as the product of small factors, Joux proposes an explicit way or method for constructing polynomials with the required form.
The initial point is observing that the elements of Fq* form a subgroup of Fq2* of order q − 1 under multiplication. This directly implies that any element α ∈ Fq* satisfies αq-1 = 1, and thus αq= α. Therefore, the q elements of Fq are all roots of the polynomial xq − x ∈ Fq2 [x], and so we have Equation A:
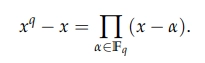
Using the Equation
Equation A shows that xq − x is a product of elements of the factor base. To use this as a relation between elements of the factor base, we require xq − x to have a fairly low degree when considered as an element of F(q2)k. This relies upon the choice of the irreducible polynomial used to represent the elements of F(q2)k as polynomials over Fq2. If I ∈ Fq2 [x] is an irreducible polynomial that divides h1xq − h0 for some h0, h1 ∈ Fq2 [x], then xq = h0/h1 in Fq2[x]/(I).
If we can find a suitable I, h0, and h1 for which h0/h1 is a polynomial of a reasonably small degree, then xq − x is an element of our factor base, as desired. Joux gives heuristic arguments to suggest that, in general, suitable irreducible polynomials do exist.
The discrete logarithms of all the components of the factor base may be found by linear algebra after we have a sufficient number of relations; this step is directly comparable to the corresponding step in the conventional index calculus approach.
However, in contrast to the conventional method, relations can be generated, and the discrete logarithms of the components of the factor base can be calculated (given some heuristic assumptions) in randomized polynomial time. This method's expensive component is finding the discrete logarithm of any field element using these discrete logarithm values. This involves a descent phase where the element whose logarithm we want to compute is defined in terms of polynomials of gradually lower degree, up until a point where the known logarithms of the element base may be employed.
Frequently Asked Questions
What is a discrete logarithm problem in cryptography?
We have a group G, g which is a group generator, and an element h that belongs to G. The discrete logarithm problem is described as finding the discrete logarithm of h to the base g in the group G. A discrete logarithm problem need not be complex. The groups determine how challenging it is to locate discrete logarithms.
Is there any difference between Index and Discrete logarithm?
No, the two terms are synonymous.
What do you mean by field characteristic?
The characteristic is the smallest number, say, n, such that n times the identity element is zero. But there is a possibility that n*1 will never be zero.
How to find if a group is cyclic?
A group G is cyclic if the group G =〈g〉, for some g ∈ G. Where g is a generator of〈g〉. If a generator g has order n, G = 〈g〉 is cyclic of order n. If a generator g has infinite order, G = 〈g〉 is infinite cyclic.
Conclusion
This blog discusses Joux’s Index Calculus for fields of small characteristics in detail. It also contains information about the discrete logarithm problem and Index calculus. We also discussed the difference between Joux’s Index calculus approach and the Traditional approach of Index calculus. We then moved forward with the frequently asked questions related to this topic.
To learn more about cryptography, check out the following articles.
To learn more about DSA, competitive coding, and many more knowledgeable topics, please look into the guided paths on Coding Ninjas Studio. Also, you can enroll in our courses and check out the mock test and problems available to you. Please check out our interview experiences and interview bundle for placement preparations.
Keep Learning, and keep growing!