Introduction
UGC NET Exam is a very popular exam in India for people interested in research. Previous Year Questions are an excellent option to learn about the exam pattern. By solving the PYQs, you will get a basic idea about your preparation.
Refer to July 2018 Paper II Part 1 here.
Refer to July 2018 Paper II Part 2 here.
Refer to July 2018 Paper II Part 3 here.
You can evaluate your weak areas and work on them to perform better in the examination. In this article, we have given the questions of UGC NET July 2018 Paper II. We have also explained every problem adequately to help you learn better.
July 2018 Paper II Part 4
76. Consider the following statements :
(a) False╞ True
(b) If α╞ (β ∧ γ) then α╞ β and α╞ γ.
Which of the following is correct with respect to the above statements?
(1) Both statement (a) and statement (b) are false.
(2) Statement (a) is true but statement (b) is false.
(3) Statement (a) is false but statement (b) is true.
(4) Both statement (a) and statement (b) are true.
Answer: 4
A |=B If and only if the sentence A=>B is valid
False |=True: False => True , always true
if A|=(B and Y) then A|=Y: (A=>(B and Y)) => (A=>Y) by constructing the truth table you will find out that it is a tautology, always true
77. Consider the following English sentence:
“Agra and Gwalior are both in India”.
A student has written a logical sentence for the above English sentence in First-Order Logic using the predicate In(x, y), which means x is in y, as follows:
In(Agra, India) V In(Gwalior, India)
Which one of the following is correct with respect to the above logical sentence?
(1) It is syntactically valid but does not express the meaning of the English sentence.
(2) It is syntactically valid and expresses the meaning of the English sentence also.
(3) It is syntactically invalid but expresses the meaning of the English sentence.
(4) It is syntactically invalid and does not express the meaning of the English sentence.
Answer: 1
The given predicate In(Agra, India) ∨ In(Gwalior, India) represent that at least one of Agra and Gwalior in INDIA so the correct representation of the given English sentence is
In(Agra, India) Λ In(Gwalior, India)
78. Consider the following two sentences:
(a) The planning graph data structure can be used to give a better heuristic for a planning problem.
(b) Dropping negative effects from every action schema in a planning problem results in a relaxed problem.
Which of the following is correct with respect to the above sentences?
(1) Both sentence (a) and sentence (b) are false.
(2) Both sentence (a) and sentence (b) are true.
(3) Sentence (a) is true but sentence (b) is false.
(4) Sentence (a) is false but sentence (b) is true.
Answer: 2
(a) The planning graph data structure can be used to give a better heuristic for a planning
problem.
This statement is correct.
Reason:
- The task of coming up with a sequence of actions that will achieve a goal is called planning.
- A special data structure known as planning graph can be used to give better heuristic estimates. A planning graph consists of a sequence of levels that correspond to time steps in the plan where 0 is the initial state.
- A planning graph once constructed is a rich source of information about the problem. A literal that does not appear in the final level of the graph cannot be achieved by any plan.
- We can estimate the cost of achieving the goal literal as the level at which it first appears in the planning graph. Planning graph allow several actions at each level whereas heuristic counts just the level and not the number of actions.
(b) Dropping negative effects from every action schema in a planning problem results in a
relaxed problem.
This statement is correct.
Reason:
- In planning, logical based description of the environment is included. Two possible developments in layered graph are: positive effects which generate facts that are positive and negative effects which are used to mark conflicts.
- Negative effects should be removed such that we only left with positive preconditions. Negative effects put restrictions on the actions due to which time increases. Dropping of negative effects from every action schema increases the number of actions and results in a relaxed problem.
79. A knowledge base contains just one sentence, ∃x AsHighAs (x, Everest). Consider the following two sentences obtained after applying existential instantiation.
(a) AsHighAs (Everest, Everest)
(b) AsHighAs (Kilimanjaro, Everest)
Which of the following is correct with respect to the above sentences?
(1) Both sentences (a) and sentence (b) are sound conclusions.
(2) Both sentences (a) and sentence (b) are unsound conclusions.
(3) Sentence (a) is sound but sentence (b) is unsound.
(4) Sentence (a) is unsound but sentence (b) is sound.
Answer: 4
The ∃x AsHighAs (x, Everest) means there is one element which is as highest as Everest.
a. AsHighAs (Everest, Everest), both are Everest so we can’t compare them.
b. AsHighAs (Kilimanjaro, Everest) means kilimanjaro which is as highest as Everest. So this is a valid statement because we are comparing Kilimanjaro with Everest.
80. Consider the set of all possible five-card poker hands dealt fairly from a standard deck of fifty-two cards. How many atomic events are there in the joint probability distribution?
(1) 2, 598, 960
(2) 3, 468, 960
(3) 3, 958, 590
(4) 2, 645, 590
Answer: 1
Number of atomic events are there in the joint probability distributionof 5 cards hand from a 52 deck of cards is calculated as shown below:
Total number of combinations possible to have a set of 5 cards from 52,
Total atomic events or count = 52C5
= 52!/5! * (52-5)!
= 52!/5! * 47!
= (48 x 49 x 50 x 51 x 52)/5!
= 311875200/120
= 2598960
81. E is the number of edges in the graph and f is the maximum flow in the graph. When the capacities are integers, the runtime of the Ford-Fulkerson algorithm is bounded by:
(1) O (E∗f)
(2) O (E1∗f)
(3) O (E∗f2)
(4) O (E2∗f2)
Answer: Marks to all
The above question was found to be ambiguous thus, marks were given to all the candidates.
82. Which of the following statements is false about the convex minimization problem?
(1) If a local minimum exists, then it is a global minimum
(2) The set of all global minima is a convex set
(3) The set of all global minima is a concave set
(4) For each strictly convex function, if the function has a minimum, then the minimum is unique
Answer: 3
The following statements are true about the convex minimization problem:
- if a local minimum exists, then it is a global minimum.
- the set of all (global) minima is convex.
- for each strictly convex function, if the function has a minimum, then the minimum is unique
83. The following LPP
Maximize z = 100x1+2x2+5x3
Subject to
14x1+x2−6x3+3x4 = 7
32x1+x2−12x3 ≤ 10
3x1−x2−x3 ≤ 0
x1, x2, x3, x4 ≥ 0
has
(1) Solution: x1=100, x2=0, x3=0
(2) Unbounded solution
(3) No solution
(4) Solution: x1=50, x2=70, x3=60
Answer: 2
B will be correct because according to the above the unbounded feasible solution can not be determined, instead, there are infinitely many solutions.
84. Digital data received from a sensor can fill up 0 to 32 buffers. Let the sample space be S={0, 1, 2, .........., 32} where the sample j denote that j of the buffers are full and
p(i) =1/561 (33 - i). Let A denote the event that the even number of buffers are full. Then p(A) is:
(1) 0.515
(2) 0.785
(3) 0.758
(4) 0.485
Answer: 1
Given,
Probability of ith buffer getting full = p(i)=1562(33−i)
Probability of all even number of buffers are full is ∑i=0,2,4,6,8,..,32p(i)=∑i=016p(2i)
P(A)=1562(33+31+29+27+....+1)
P(A)=1562×289=0.51423
85. The equivalence of
¬ ∃x Q(x) is:
(1) ∃ x ¬ Q(x)
(2) ∀x ¬ Q(x)
(3) ¬ ∃x ¬ Q(x)
(4) ∀x Q(x)
Answer: 2
The expression ¬ ∃x Q(x) is equivalent to ∀x ¬ Q(x), since we can replace for all with for each.
86. If Ai = {−i, ... −2,−1, 0, 1, 2, . . . . . i}
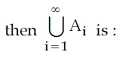
(1) Z
(2) Q
(3) R
(4) C
Answer: 1
The resultant magnitude will include only the integers as the A set includes Z.
87. Match the following in List - I and List - II, for a function f:
List - I
(a) ∀x ∀y (f (x)=f (y) → x=y)
(b) ∀y ∃ x (f (x)=y)
(c) ∀x f (x)=k
List - II
(i) Constant
(ii) Injective
(iii) Surjective
Code:
(a) (b) (c)
(1) (i) (ii) (iii)
(2) (iii) (ii) (i)
(3) (ii) (i) (iii)
(4) (ii) (iii) (i)
Answer: 4
∀x∀y (f(x) = f(y) → x = y), that means if two functions maps same value then input of the functions should be same. This is definition of injective (or one-to-one) function.
An injective function or injection or one-to-one function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain.
∀y∃x (f(x) = y), which means for all y, there is a mapping function from x. This is the definition of the surjective (or onto) function.
A function f from a set X to a set Y is surjective (or onto), or a surjection, if for every element y in the codomain Y of f there is at least one element x in the domain X of f such that f(x) = y.
∀x f(x) = k, which means for all x, the output or mapping is only k and never changes. This is the definition of the constant function.
A constant function is a function whose (output) value is the same for every input value. For example, the function is a constant function because the value of is 4 regardless of the input value.
Therefore, option (D) a – (ii), b – (iii), c – (i) is correct.
88. Which of the relations on {0, 1, 2, 3} is an equivalence relation?
(1) { (0, 0) (0, 2) (2, 0) (2, 2) (2, 3) (3, 2) (3, 3) }
(2) { (0, 0) (1, 1) (2, 2) (3, 3) }
(3) { (0, 0) (0, 1) (0, 2) (1, 0) (1, 1) (1, 2) (2, 0) }
(4) { (0, 0) (0, 2) (2, 3) (1, 1) (2, 2) }
Answer: 2
A relation is an equivalence only iff the relation has reflexive, symmetric, and transitive properties. Therefore,
(A) Because of (0, 2) and (2, 3), then it should have (0, 3) which is not the relation. Also, (3, 2) and (2, 0), then it should have (3, 0) which is not the relation. Therefore, this given relation is transitive, so can be an equivalence relation.
(B) It is reflexive, symmetric, and transitive, so equivalence relation. It is diagonal relation and a diagonal relation is always an equivalence relation.
(C) This relation is neither reflexive, nor symmetric, so it can not be reflexive relation.
(D) It is not reflexive, not symmetric and not transitive, so it can not be reflexive relation.
UGC has taken this question from Kenneth Rosen-6th edition (Ques-1, Chapter- 8.5).
89. Which of the following is an equivalence relation on the set of all functions from Z to Z?
(1) { (f, g) | f(x)−g(x)=1 ∀x e Z }
(2) { (f, g) | f(0)=g(0) or f (1)=g(1) }
(3) { (f, g) | f(0)=g(1) and f (1)=g(0) }
(4) { (f, g) | f(x)−g(x)=k for some k ∈ Z }
Answer: 4
(1) This relation has none of the three properties. It is not reflexive, since f(x) – f(x) = 0 ≠ 1. It is not symmetric, since if j(x)- g(x) = 1, then g(x)- f(x) = -1 ≠ 1. It is not transitive, since if f(x)- g(x) = 1 and g(x) – h(x) = 1, then f(x) – h(x) = 2 ≠ 1.
(2) This is not an equivalence relation because it is not transitive. Let f(x) = 0, g(x) = x, and h(x) = 1 for all x E Z. Then f is related tog since f(0) = g(0), and g is related to h since g(1) = h(1), but f is not related to h since they have no values in common. By inspection we see that this relation is reflexive and symmetric.
(3) This relation is not reflexive, since there are lots of functions f (for instance, f(x) = x) that do not have the property that f(0) = f(1). It is symmetric by inspection (the roles of f and g are the same). It is not transitive. For instance, let f(0) = g(1) = h(0) = 7, and let f(0) = g(0) = h(1) = 3; fill in the remaining values arbitrarily. Then f and g are related, as are g and h, but f is not related to h since 7 ≠ 3.
(4) This is an equivalence relation. Two functions are related here if they differ by a constant. It is clearly reflexive (the constant is 0). It is symmetric, since if f (x) – g(x) = k, then g(x) – f (x) = -k. It is transitive, since if f(x) – g(x) = k1 and g(x) – h(x) = k2 , then f(x) – h(x) = k3 , where k3 = k1 + k2 (add the first two equations).
90. Which of the following statements is true?
(1) (Z, ≤ ) is not totally ordered
(2) The set inclusion relation ⊆ is a partial ordering on the power set of a set S
(3) (Z, ≠ ) is a poset
(4) The directed graph
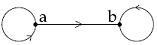
is not a partial order
Answer: 2
Option 1: (Z, ≤) is not totally ordered
This is false. As ≤ is totally ordered. A partially ordered set with comparison is known as a totally ordered set. Consider the set contains elements {1, 2, 3, 4}. This represents a totally ordered set. As 1<= 2, 2<=3, 3< = 4.
Option 2: The set inclusion relation ⊆ is a partial ordering on the power set of a set S
If we consider the set S = {a, b} . So possibilities with this set are {Ø, a, b, ab}. As, subset relation is reflexive, antisymmetric and transitive. So, it is partially ordered. Because if a is a subset of b, then b is a superset of a.
Option 3: (Z, ≠ ) is a poset
It is not a partially ordered set. As it follows symmetric property. For example, if a is not equal to b, then b is also not equal to a. It can not be a poset. The given statement is incorrect.
Option 4: The directed graph is not a partial order
This statement is incorrect. This graph represents partial order. It can be represented as:
It is satisfying the property of a partially ordered set. So, given directed graph is a poset. It is reflexive, antisymmetric and transitive.
91. CMOS is a Computer Chip on the motherboard, which is:
(1) RAM
(2) ROM
(3) EPROM
(4) Auxillary storage
Answer: 1
A complementary metal-oxide-semiconductor(CMOS) is a random access memory that stores computer start-up information which is used by BIOS. CMOS memory in a computer is a type of non-volatile RAM (NVRAM) that stores BIOS settings and date/time information.
So, Option 1 is the correct answer.
92. In RS flip-flop, the output of the flip-flop at the time (t+1) is the same as the output at time t, after the occurrence of a clock pulse if:
(1) S=R=1
(2) S=0, R=1
(3) S=1, R=0
(4) S=R=0
Answer: 4
S = R = 0 is the normal resting condition of the flip-flop. It has no effect on the output state of the flip-flop. Both Q and Q¯ outputs remain in the logic state they were in prior to this input condition.
93. Match the terms in List - I with the options given in List - II :
List - I
(a) Decoder
(b) Multiplexer
(c) Demultiplexer
List - II
(i) 1 line to 2n lines
(ii) n lines to 2n lines
(iii) 2n lines to 1 line
(iv) 2n lines to 2n−1 lines
Code:
(a) (b) (c)
(1) (ii) (i) (iii)
(2) (ii) (iii) (i)
(3) (ii) (i) (iv)
(4) (iv) (ii) (i)
Answer: 2
Decoder = n to 2^n
Mux = Many to One i.e. 2^n to 1
De Mux = One to Many i.e. 1 to 2^n
94. What does the following logic diagram represent?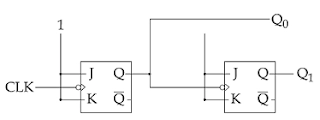
(1) Synchronous Counter
(2) Ripple Counter
(3) Combinational Circuit
(4) Mod 2 Counter
Answer: 2
Ripple Counter: Ripple counter is an Asynchronous counter. It got its name because the clock pulse ripples through the circuit. An n-MOD ripple counter contains n number of flip-flops and the circuit can count up to 2 n values before it resets itself to the initial value.
Given Flip-Flop Logic, the diagram represents the Ripple counter.
So, option 2 is the correct answer
95. The hexadecimal equivalent of the binary integer number 110101101 is:
(1) D 2 4
(2) 1 B D
(3) 1 A E
(4) 1 A D
Answer: 4
Group the given number in a subgroup of 4 from the right and assign the alphabet when it exceeds 1001:
1010 – A
1011 – B
1100 – C
1101 – D
1110 – E
1111 – F
Given number is 110101101:
1101 – D
1010 – A
1 – 1
The hexadecimal equivalent is 1AD.
96. Perform the following operation for the binary equivalent of the decimal numbers
(−14)10 + (−15)10
The solution in 8-bit representation is:
(1) 11100011
(2) 00011101
(3) 10011101
(4) 11110011
Answer: 1
(−14)10+(−15)10 = (-29)10
Now 29 in binary(8 bit) is 00011101 But the number is negative.
Take 1’s complement 11100010 and 1 to it
I.e. 11100011.
97. Match the items in List - I and List - II :
List - I
(a) Interrupts which can be delayed when a much highest priority interrupt has occurred
(b) Unplanned interrupts which occur while executing a program
(c) Source of interrupt is in phase with the system clock
List - II
(i) Normal
(ii) Synchronous
(iii) Maskable
(iv) Exception
Code:
(a) (b) (c)
(1) (ii) (i) (iv)
(2) (ii) (iv) (iii)
(3) (iii) (i) (ii)
(4) (iii) (iv) (ii)
Answer: 4
The hardware interrupts which can be delayed when a much high priority interrupt has occurred at the same time- a Maskable interrupt.
Unplanned interrupts while executing a program are called Exceptions.
The Source of interruption is in phase with the clock: Synchronous.
98. Which of the following mapping is not used for the mapping process in cache memory?
(1) Associative mapping
(2) Direct mapping
(3) Set-Associative mapping
(4) Segmented-page mapping
Answer: 4
There is three types of cache mapping:
- Direct mapping.
- Associative mapping.
- Set Associative mapping
99. Simplify the following using K-map:
F (A, B, C, D) = Σ (0, 1, 2, 8, 9, 12, 13)
d (A, B, C, D) = Σ (10, 11, 14, 15)
d stands for don’t care condition.
(1) A+B’ D’ + BC
(2) A+B’ D’ + B’ C’
(3) A’+B’ C’
(4) A’+B’ C’+B’ D’
Answer: 2
The simplification of the above will be A+B’ D’ + B’ C’ using K-Maps simplification.
100. In 8085 microprocessor, what is the output of following program?
LDA 8000H
MVI B, 30H
ADD B
STA 8001H
(1) Read a number from the input port and store it in memory
(2) Read a number from the input device with address 8000H and store it in memory at location 8001H
(3) Read a number from memory at location 8000H and store it in memory location 8001H
(4) Load A with data from the input device with address 8000H and display it on the output device with address 8001H
Answer: 4
LDA 8000H,
- Above instruction transfer data from memory location 8000H to Accumulator
MVI B, 30H
ADD B
- Above 2 instruction, moves 30H to Register B and adds it to Accumulator. So basically the contents of the Accumulator are incremented by 30H
STA 8001H
- Finally, the contents of the Accumulator are stored in memory location 8001H
None of the choices includes the 'addition operation'. *Choice 3 looks to be most appropriate*.
Generally IN/OUT are used for writing to devices port (8bit addresses), so I don't think Choice 4 is the best answer.




