Table of contents

Introduction

Problem Statement

Approach 1: Dynamic Programming

3.1.

Implementation

3.2.

Complexity Analysis

Approach 2: Greedy Algorithm

4.1.

Implementation

4.2.

Analysis of Complexity

FAQ'S

Key Takeaways

Last Updated: Mar 27, 2024

Jump Game II

Author Soumya Agrawal

Introduction

This problem is based on one of the popular topics of Data Structures. I.e., Dynamic Programming, and Greedy Algorithms. Dynamic programming is an optimization for recursion. In recursion, we calculate the same calculation again and again, but in DP, this problem can be overcome.

Greedy algorithms use a technique to build the solution piece by piece and choose the piece which offers the most immediate benefit.

The Jump Game II is a problem where we will find minimum steps to reach the final index from the starting index.

We will see different approaches for solving this problem.

Let's move on to our problem statement.

Problem Statement

We are given an array, standing on the first index and taking a minimum number of steps to reach the last index. Every integer in the array represents the maximum number of steps a person can take.

Our goal is to get the minimum jumps from source to destination.

You can understand it like this: suppose your first index is your house, and the destination you have to reach is your last index. Now you have to tell how many minimum steps. At each step, you will be given how many steps you can take.

Note:

The array of non-negative integers.
You will always reach the last index.

For example:

Input:

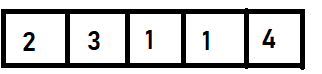
Output:

Let me give you a brief about this example through a pictorial representation.

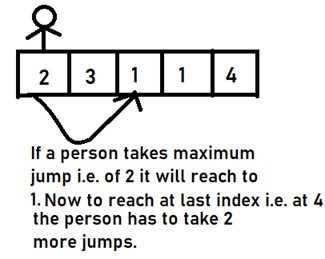
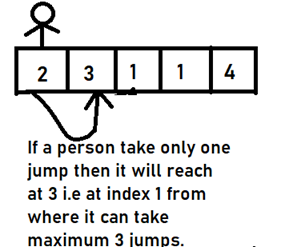
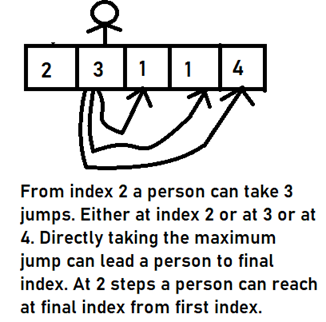
This problem is easy if we have to do it in O(n2) time, but it becomes challenging to solve it in O(n) time complexity.

Try to solve it out for another example:

Input:

5,9,3,2,1,0,2,3,3,1,0

What will be the minimum jumps to reach the last index??

From index 0 we can at max go 0 + 5 = 5
From index 1, we can at max go 1 + 9 = 10
From index 2, we can at max go 2 + 3 = 5,
From index 3,we can at max go 3 + 2 = 5
From index 4 we can at max go, 4 + 1 = 5
From index 5, we can at max go 5 + 0 = 5
From index 6, we can at max go 6 + 2 = 8
From index 7, we can at max go 7 + 3 = 10
From index 8, we can at max go 8 + 3 = 11 (this is the last index)
First, we will check how to reach 8.

Minimum index to reach 8

index 0,we can at max go 0 + 5 = 5

index 1, we can at max go 1 + 9 = 10

We have to first reach the index 1

Minimum index to reach at index 1

index 0,we can at max go 0 + 5 = 5, yes. So, 3 total jumps.

If the problem statement is clear, let's move to our approach.

Note: Please try to solve Jump Game II on Coding Ninjas Studio before stepping into the solution

Approach 1: Dynamic Programming

The approach we will be using to find the minimum jumps is Dynamic Programming. This approach will not be an efficient one.

We will create a DP array of n+1 where n is the number of elements.
Set all the indexes of the array to the maximum value.
Initialize the first index of the array as '0'.
Iterate the array with the help of loops, keep the total count to reach the last index, and find the minimum jumps.
Print the total number of jumps.

Implementation

public int jump(int[] nums) {

  int n = nums.length;
  //creating the dp array where count of jumps are stored
  int[] dp = new int[n + 1];

  //filling the dp array with the max value
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;

  //loop for counting the minimum jumps
  for (int i = 1; i < n; i++) {
  for (int j = 0; j < i; j++) {
  if (j + nums[j] >= i) {
  //min function for finding the minimum
dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
}
  return dp[n - 1];

  // Driver Code
  public static void main(String[] args)
{
  int[] arr = { 2,3,0,1,4 };
  int size = arr.length;
System.out.println("Minimum jumps is"+jump(arr, size));
}

}

Output:

The minimum jump is 2.

Complexity Analysis

Time Complexity: The time complexity to solve this approach is O(n^2). Due to the nested traversal of the array.
Space Complexity: The space complexity will be O(n). To store the DP, linear space is needed.

Check out Longest Common Substring

Approach 2: Greedy Algorithm

We will try to find out the total number of minimum jumps in an efficient way.

Given array arr = 1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9

max=arr[0] which means arr[0] = 1 so the maximum index we can reach is 1.
steps=arr[0]-> arr[0] = 1, We can take '1' step.
jump= 1; we are making our first jump.(Here jump is taken as a variable)
Now, starting iteration from index 1:

First, we will check that we have reached the end of the array or not. Otherwise, we will increment the jump variable.

if (i == arr.length - 1)

return jump;

2. Update the max. Which will be equal to max and i+arr[i].

max= Math.max(max, i+arr[i]);

3. To get the current index, we use steps, so steps have to be decreased.

step--;

4. We must have used a jump if there are no more steps (i.e., steps=0). As a result, boost your jump. Because we know that reaching max is attainable somehow, we initialize the steps to the number of steps required to reach max from point i. However, before re-initializing steps, we must first determine whether it is becoming zero or negative. It is not possible to go any further in this case.

Implementation

//To find the minimum jumps

class Solution {
static int jump(int arr[])
{
if (arr.length <= 1)
return 0;

if (arr[0] == 0)
return -1;

//variables for finding out the jumps needed
int max = arr[0];
int steps = arr[0];
int jump = 1;

//traversing of the array
for (int i=1; i <arr.length; i++) {
//to find out whether we have reached the last index or not.
if (i == arr.length - 1)
return jump;

//update max
max = Math.max(max, i+arr[i]);

// To reach the current index we use steps
steps--;

// If no further steps left
if (steps == 0) {
// we must have used a jump
jump++;

if (i >= max)
return -1;

//re-initialize the steps for max to reach from position i
steps = max - i;
}
}

return -1;
}

// main method
public static void main(String[] args)
{
int arr[] = new int[] { 1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9 };

System.out.println(jump(arr));
}
}

Output:

Analysis of Complexity

Time Complexity: The time complexity will be O(n).
Space Complexity: O(1). No space is required in this approach.

FAQ'S

1). What do you mean by Dynamic Programming?

In dynamic programming, we create subproblems out of the main problem and make the computer remember the solutions of the subproblems to use in the result directly.

2). What are the time complexities to solve this problem?

The naive approach will take O(n^2) time complexity, and an efficient approach will take O(n) time.

Key Takeaways

In this blog, we discuss how to find the total number of minimum jumps. We see the implementation of Jump Game II in Java language. For more clarity, you can practice more questions similar to this, like Jump Game, Jump Game III, and many more. To make your concepts more clear related to dynamic programming, you cannot check out here.

Check out this problem - Minimum Coin Change Problem

You can also have a view of the Data Structures and Algorithms-guided path to start your preparation from scratch.

Happy Learning!

Live masterclass