June 2013 Paper-II Part-2

Introduction

UGC NET Exam is a very popular exam in India for people interested in research. Previous Year Questions are an excellent option to learn about the exam pattern. By solving the PYQs, you will get a basic idea about your preparation. You can evaluate your weak areas and work on them to perform better in the examination. In this article, we have given the questions of UGC NET 2013 June Paper-II. We have also explained every problem adequately to help you learn better.

Note: This article contains Q.No. 26 to Q.No. 50 out of the 50 questions asked in NET June 2013 paper II. The solutions to Q.No. 1 to Q.No. 25 can be found in June 2013 Paper-II Part-1 article.

June 2013 paper II

1. Given an open address hash table with load factor a < 1, the expected number of probes in a successful search is
   (A) Atmost  1/α ln (1-α/α)
   (B) Atmost  1/α ln (1/1-α)
   (C) Atleast  1/α ln (1/1-α)
   (D) Atleast  1/α ln (α/1-α)
   Answer: B
   Given an open-address hash table with load factor α = n/m < 1, the expected number of probes in a successful search is at most (1/α) ln (1/(1-α)), assuming uniform hashing and assuming that each key in the table is equally likely to be searched for.
    
2. For a B-tree of height h and degree t, the total CPU time used to insert a node is
   (A) O(h log t)  (B) O(t log h)
   (C) O(t2h)       (D) O(th)
   Answer: D
   The number of disk pages accessed by B-tree search is O(h)
   Time taken by each node is O(t)
   Therefore, total CPU time = O(t h)
    
3. The time complexity to build a heap with a list of n numbers is
   (A) O(log n)    (B) O(n)
   (C) O(n log n)   (D) O(n2)
   Answer: B
   The time complexity of building a heap is asymptotically O(n). So, the correct answer is option B.
    
4. The value of postfix expression:
   8 3 4 + - 3 8 2 / + * 2 $ 3+ is
   (A) 17           (B) 131
   (C) 64           (D) 52
   Answer: D
   The above-given postfix expression is equivalent to
   { [ (8-(3+4))*(3+(8/2))] $ 2 } +3
   = { [ (1)*(7)] $ 2 } + 3
   = { 7 $ 2 } + 3
   = 49 + 3
   = 52
    
5. Consider the following statements for priority queue:
   S1: It is a data structure in which the intrinsic ordering of the elements does determine the result of its basic operations.
   S2: The elements of a priority queue may be complex structures that are ordered on one or several fields.
   Which of the following is correct?
   (A) Both S1 and S2 are incorrect.
   (B) S1 is correct and S2 is incorrect.
   (C) SI is incorrect and S2 is correct.
   (D) Both S1 and S2 are correct.
   Answer: D
   A priority queue is a data structure in which the intrinsic ordering of the elements does determine the result of its basic operations and its elements may be complex structures that are ordered on one or several fields
    
6. Repository of information gathered from multiple sources, storing under unified scheme at a single site is called as
   (A) Data mining                 (B) Meta data
   (C) Data warehousing (D) Database
   Answer: C
   Data mining is finding anomalies, patterns, and correlations within large data sets to predict outcomes.
   Metadata is the data that provides information about other data.
   Data warehousing is the repository of information gathered from multiple sources.
   The database is information, set up for easy access, management, and updating.
   So the correct answer is Data warehousing.
    
7. The task of correcting and pre processing data is called as
   (A) Data streaming   (B) Data cleaning
   (C) Data mining        (D) Data storming
   Answer: B
   Data cleaning is the process of detecting and correcting inaccurate data.
    
8. Using data p=3, q=11, n=pq, d=7  in RSA algorithm find the cipher text of the given plain text SUZANNE
   (A) BUTAEEZ            (B) SUZANNE
   (C) XYZABCD           (D) ABCDXYZ
   Answer: A
   n = p*q = 33
   Φ = (p-1) * (q-1)
   d =7
   e=3 (e*d = 1 mod 20)
   Message M= SUZANNE
   Taking A=1, B=2, C=3,.......,A=27,B=28,.....
   Cipher text= (M^e mod n)
   S=19 => cipher= 19³ mod 33 = 28 = B
   U=21 => cipher= 21³ mod 33 = 21 = U
   After doing this we will get
   BUTAEEZ
    
9. The relation "divides" on a set of positive integers is ..................
   (A) Symmetric and transitive
   (B) Anti symmetric and transitive
   (C) Symmetric only
   (D) Transitive only
   Answer: B
   The relation “divides” on a set of positive integers is anti-symmetric and transitive.
    
10. Give as good a big-O estimate as possible for the following functions:
    (nlogn+n²)(n³+2) and (n!+2n)(n³+log(n²+ 1))
    (A) O(n⁵+2n²) & O(n³*n!)
    (B) O(n⁵) & O(n³*2n)
    (C) O(n⁵) & O(n³*n!)
    (D) O(n⁵+2n²) & O(n³*2n)
    Answer: C
    (n logn + n²) is upper bounded by O(n²)
    (n³ + 2) is upper bounded by O(n³)
    So, (nlogn+n²)(n³+2) will be upper bounded by O(n² x n³) = O(n⁵)
    (n!+2n) is upper bounded by O(n!)
    (n³+log(n²+ 1)) is upper bounded by O(n³)
    So, (n!+2n)(n³+log(n²+ 1)) can be written asymptomatically as O(n³*n!)
     
11. A test contains 100 true/false questions. How many different ways can a student answer the questions on the test, if the answer may be left blank also.
    (A) ¹⁰⁰P₂          (B) ¹⁰⁰C₂    
    (C) 2¹⁰⁰           (D) 3¹⁰⁰
    Answer: D
    There are three possibilities to answer a question. Mark it True, mark it false or leave it blank. And there are 100 such questions. So the total number of possibilities will be
    3 * 3 * ……(100 times)..... * 3 * 3
    = 3¹⁰⁰
     
12. Which of the following connected simple graph has exactly one spanning tree?
    (A) Complete graph  (B) Hamiltonian graph
    (C) Euler graph                     (D) None of the above
    Answer: D
    Complete graph has n^n-2 spanning trees
    Hamiltonian graph and Euler graph will get more than one spanning tree. 
    So the answer will be D
     
13. How many edges must be removed to produce the spanning forest of a graph with N vertices, M edges and C connected components?
    (A) M+N-C      (B) M-N-C
    (C) M-N+C     (D) M+N+C
    Answer: C
    A spanning forest is a set of spanning trees, one for each connected component. The number of edges that need to be removed to make a spanning forest is M-N+C.
     
14. Which of the following shall be a compound proposition involving the propositions p, q and r, that is true when exactly two of the p, q and r are true and is false otherwise?
    (A) (p∨q∧˥r) ∨ (p∨q∧r) ∧ (˥p∧q∨r)
    (B) (p∧q∨r) ∧ (p∧q∧r) ∨ (˥q∨˥p∧˥r)
    (C) (p∧q∧˥r) ∨ (p∨˥q∧r) ∨ (˥p∧q∧r)
    (D) (p∨r∧q) ∨ (p∧q∧r) ∨ (˥p∧q∧r)
    Answer: C
    In the given options C is the only one where two of the p, q, r are true and are false otherwise and the overall proposition is true.
    (p∧q∧˥r) -> p and q are true
    (p∨˥q∧r) -> p and r are true
    (˥p∧q∧r) -> q and r are true
    The overall proposition is true
     
15. The truth value of the statements:
    ∃!xP(x)→∃xP(x) and ∃!x˥P(x)→˥∀xP(x), (where the notation ∃!xP(x) denotes the proposition "There exists a unique x such that P(x) is true'') are:
    (A) True and False   (B) False and True
    (C) False and False (D) True and True
    Answer: D
    ∃ is called the existential quantifier. It represents “there exists” or “for some”.
    The existential quantification of P(x) is “P(x) for some values x in the universe”, or “There exists a value for x such that P(x) is true”, which is written as ∃xP(x).
    So the statement ∃!xP(x)→∃xP(x) is true
    Now, according to DeMorgan’s law for quantifiers,
    ∀xP(x) ≡ ∃x˥P(x)
    ∃xP(x) ≡ ∀x˥P(x)
    So, the statement ∃!x˥P(x)→˥∀xP(x) is also true.
     
16. How many different Boolean functions of degree 4 are there?
    (A) 2⁴   (B) 2⁸
    (C) 2¹² (D) 2¹⁶
    Answer: D
    Number of boolean expressions= 2 ^ 2ⁿ = 2 ^ 2⁴ = 2¹⁶
     
17. A Boolean operator Ө  is defined as follows:
    1Ө1=1, 1Ө0=0, 0Ө1=0 and 0Ө0=1
    What will be the truth value of the expression (xӨy)Өz = xӨ(yӨz)?
    (A) Always false
    (B) Always true
    (C) Sometimes true
    (D) True when x, y, z are all true
    Answer: B
    Below given is a truth table. It consists of all the possible values that we can get from both the expressions i.e. (xӨy)Өz and xӨ(yӨz)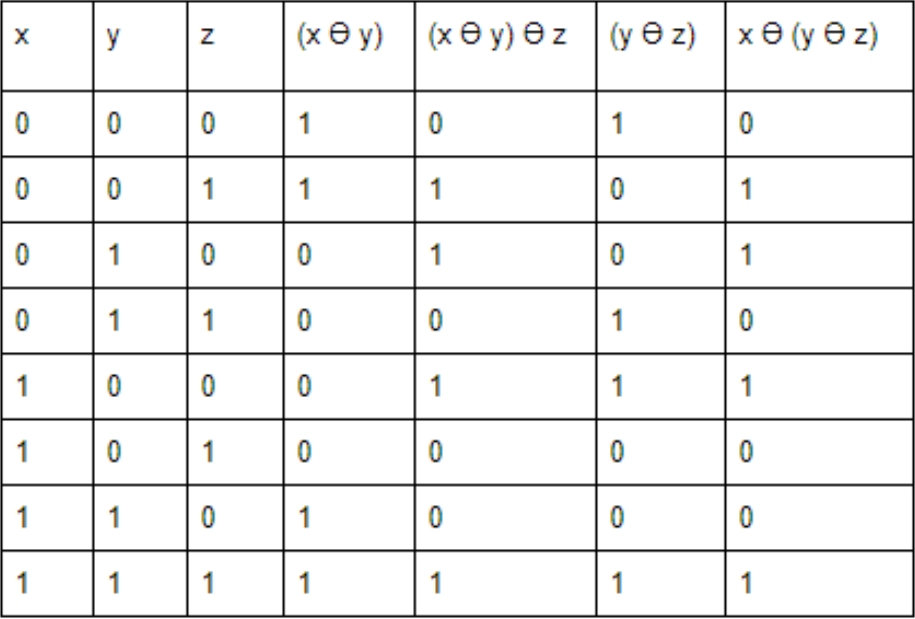
    
    From the above truth table, we can observe that the value of both the expressions is always the same. So the value of (xӨy)Өz = xӨ(yӨz) will be always true.
     
18. Which one of the following is decimal value of a signed binary number 1101010, if it is in 2's complement form?
    (A) -42          (B) - 22
    (C) -21            (D) -106
    Answer: B
    Given binary number: 1101010
    1’s complement of this number will be 1010101 
    Adding 1 to the LSB, we get 1010110= (-22)
    In the above operations, the sign bit remains unchanged.
     
19. A set of processors P1, P2, ......, Pk can execute in parallel if Bernstein's conditions are satisfied on a pair wise basis; that is
    P1 || P2 || P3 || ..... || Pk if and only if:
    (A) Pi || Pj for all i ≠ j
    (B) Pi || Pj for all i = j+1
    (C) Pi || Pj for all i ≤ j
    (D) Pi || Pj for all i ≥ j
    Answer: A
    Bernstein’s Condition:
    1. If process Pi writes to a memory cell Mi, then no process Pj can read the cell Mi.
    2. If process Pi read from a memory cell Mi, then no process Pj can write to the cell Mi.
    3. If process Pi writes to a memory cell Mi, then no process Pj can write to the cell Mi.
     
20. When a mobile telephone physically moves from one to another cell, the base station transfers ownership to the cell getting strongest signal. This process is known as.................
    (A) handoff                (B) mobile switching
    (C) mobile routing    (D) cell switching
    Answer: A
    When a mobile telephone physically moves from one to another cell, the base station transfers ownership to the cell getting the strongest signal, this is called Handoff.
     
21. A virtual memory based memory management algorithm partially swaps out a process. This is an example of
    (A) short term scheduling            (B) long term scheduling
    (C) medium term scheduling          (D) mutual exclusion
    Answer: C
    Short-term scheduler- selects which process should be executed next and allocates CPU
    Medium-term scheduler- it is a part of swapping. It removes the processes from memory and reduces the degree of multiprogramming.
    Long-term scheduler- determines which programs are admitted to the system for processing.
    Mutual exclusion is irrelevant in this question.
    So the answer is medium-term scheduling.
     
22. Assuming that the disk head is located initially at 32, find the number of disk moves required with FCFS if the disk queue of I/O block requests are 98, 37, 14, 124, 65, 67:
    (A) 310            (B) 324
    (C) 320           (D) 321
    Answer: D
    We have to calculate disk moves on each I/O block request.
    (98-32) + (98-37) + (37-14) + (124-14) + (124-65) + (67-65)
    = 321
    So the total number of disk moves is 321.
     
23. Let the page fault service time be 10 millisecond(ms) in a computer with average memory access time being 20 nanosecond(ns). If one page fault is generated for every 106 memory accesses, what is the effective access time for memory?
    (A) 21 ns        (B) 23 ns
    (C) 30 ns        (D) 35 ns
    Answer: C
    EA = (p)*(page fault service time) + (1-p)*(Memory access time)
    Where EA= Effective Access time for memory
    And p=page fault rate
    EA = 10^-6 * 10 * 10⁶ + (1-10^-6)*20
    ≃ 29.9 ns
    ≃ 30ns
     
24. Consider the following UNIX command:
    sort <in> temp; head -30 <temp; rm temp
    Which of the following functions shall be performed by this command?
    (A) Sort, taking the input from "temp", prints 30 lines from temp and delete the file temp
    (B) Sort the file "temp", removes 30 lines from temp and delete the file temp
    (C) Sort, taking the input from "in" and writing the output to "temp" then prints 30 lines from temp on terminal. Finally "temp" is removed.
    (D) Sort, taking the input from 'temp" and then prints 30 lines from "temp" on terminal. Finally "temp" is removed.
    Answer: C
    sort <in> temp -> Sort, taking the input from ‘in’ and writing the output to ‘temp’
    Head -30 <temp -> prints 30 lines from temp on terminal
    rm temp -> temp is removed
     
25. The mv command changes
    (A) the inode
    (B) the inode-number
    (C) the directory entry
    (D) both the directory entry and the inode
    Answer: C
    mv (move) is a UNIX command used to move one or more files or directories from one place to another.