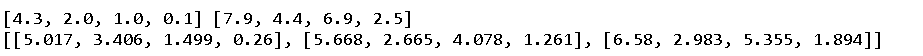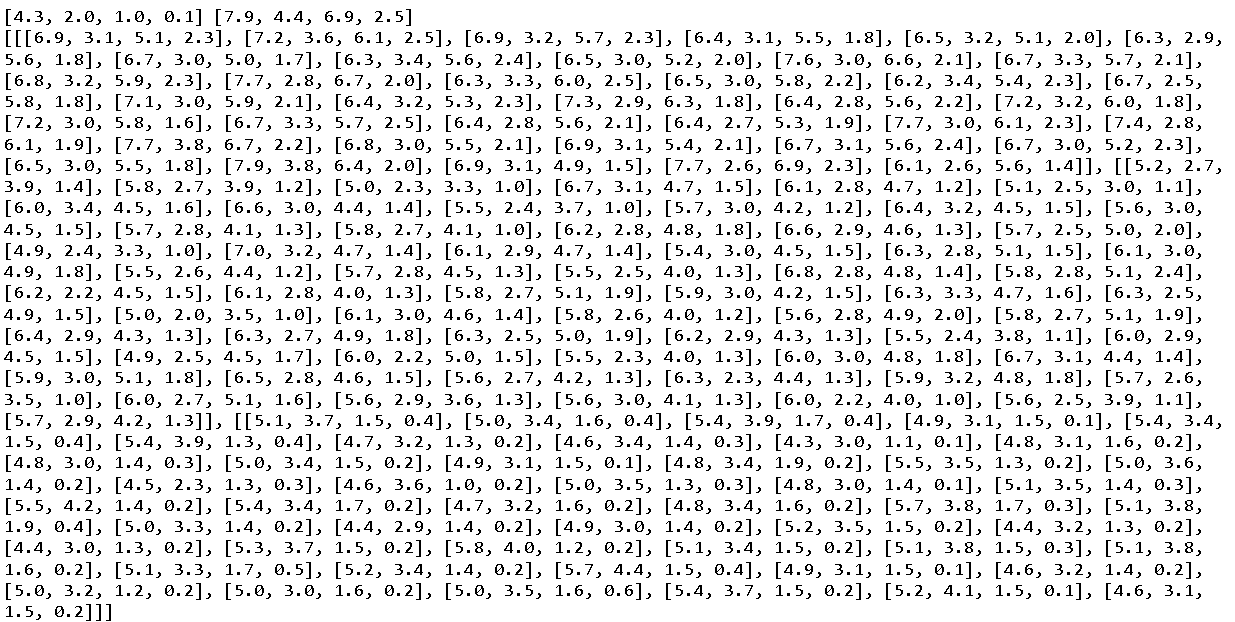K-mean Algorithm

Introduction

K-Means Clustering is an unsupervised learning algorithm used in machine learning and data science to handle clustering problems. We will study what the K-means clustering method is, how it works, and how to implement it in Python in this topic.

K-Means Algorithm

We're provided a data set of items with specific characteristics and values for these characteristics (like a vector). The goal at hand is to sort things into groups. The K-means algorithm, an unsupervised learning algorithm, will be used.

Overview

(Thinking of items as points in an n-dimensional space will assist.) The algorithm divides the objects into k groups based on their similarity. We'll use the euclidean distance as a measurement to calculate that similarity.

The following is how the algorithm works:

To begin, we randomly assign k points, known as means.

We assign each item to the nearest mean and update the mean's coordinates, the averages of the objects set to that mean thus far.

We continue the process for a predetermined amount of iterations till we have clusters.

The " points " stated above are called means because they include the mean values of the things grouped in them, the "points" stated above are called means. We have a variety of possibilities for establishing these mechanisms.

Initializing the means at random elements in the data set is straightforward. Another option is to put the means at random values between the data set's bounds (for a feature x, if the items have values in [0,3], we will initialize the means with values for x at [0,3]).

We'll read the information from the file and save it to a list(refer to data). The item values for the features are contained in each element of the list, which is another list. This is accomplished using the following function:

def ReadData(fileName):

# Read the file, splitting by lines
f = open(fileName, 'r');
lines = f.read().splitlines();
f.close();

items = [];

for i in range(1, len(lines)):
line = lines[i].split(',');
itemFeatures = [];

for j in range(len(line)-1):

# Convert feature value to float
v = float(line[j]);

# Add feature value to dict
itemFeatures.append(v);

items.append(itemFeatures);

shuffle(items);

return items;

You can also try this code with Online Python Compiler

Run Code

Initialize Means

We want to set the values of each means in the range of the item's feature values. We must determine the minimum and maximum values for each feature. This is accomplished using the following function:

def FindColMinMax(itms):
n = len(itms[0]);
mnma = [sys.maxint for i in range(n)];
maxima = [-sys.maxint -1 for i in range(n)];

for item in items:
for f in range(len(item)):
if (item[f] < minima[f]):
minima[f] = item[f];

if (item[f] > maxima[f]):
maxima[f] = item[f];

return minima,maxima;

You can also try this code with Online Python Compiler

Run Code

The variables minima and maxima are lists that hold the items' minimum and maximum values, respectively. We set the feature values of each mean at random between the appropriate minimum and maximum in the two lists above:

def InitializeMeans(tms, K, cMn, cMx):

# To Initialize means randomly in the range
# max and min of each feature/column
ftures = len(tms[0]); #features of each cluster
mns = [[0 for i in range(ftures)] for l in range(K)];

for mn in mns:
for i in range(len(mn)):

# Set value to float randomly
# (adding +-one to prevent a wide variation  of mn)
mn[i] = uniform(cMin[i]+1, cMax[i]-1);

return means;

You can also try this code with Online Python Compiler

Run Code

Euclidean Distance

We'll utilize the euclidean distance as a similarity metric for our data collection.

def EucldeanDistance(X, Y):
S = 0; # The sum of the euclidean distance
for i in range(len(X)):
S += math.pow(x[i]-y[i], 2)

#The square root of the sum
return math.sqrt(S)

You can also try this code with Online Python Compiler

Run Code

Update Means

To update a mean, we must first determine the average value for each feature across all objects in the mean/cluster. We can either add all the values and divide by the number of items, or we can use a more elegant technique. By doing the following, we can calculate the new average without having to re-add all of the values: 

m = (m*(n-1)+x)/n

You can also try this code with Online Python Compiler

Run Code

where m is the feature's mean value, n is the cluster's number of items, and x is the additional item's feature value. To get the new mean, we repeat the process for each feature.

def UpdateMean(n,mean,item):
for i in range(len(mean)):
m = mean[i];
m = (m*(n-1)+item[i])/float(n);
mean[i] = round(m, 3);

return mean;

You can also try this code with Online Python Compiler

Run Code

Classify Items

We must create a function that will classify an item into a group or cluster. We will find the item's similarity to each mean and classify it according to the closest one.

def Classify(mns,itm):

# To classify item to the mean with minimum distance
mnmm = sys.maxint;
ndx = -1;

for i in range(len(means)):

# Find distance from item to mean
dis = EuclideanDistance(item, means[i]);

if (dis < minimum):
minimum = dis;
index = i;

return index;

You can also try this code with Online Python Compiler

Run Code

Find Means

To find the means, we'll loop through all objects, classify them into clusters, and update the cluster's mean. The process will be repeated for a set number of iterations. If no item changes classification between two iterations, we halt the procedure because the algorithm has found the best answer.

The following function takes k (the desired number of clusters), the items, and the maximum number of iterations as inputs and returns the means and clusters. The array belongsTo stores an item's classification, whereas clusterSizes stores the number of elements in a cluster.

def CalculateMeans(k,items,maxIterations=100000):

# Find the minima and maxima for columns
cMin, cMax = FindColMinMax(items);

# Initialize means at random points
mns = InitializeMeans(tms,k,cMin,cMax);

# Initialize clusters
# for the list to hold  the items
cluster_sizes= [0 for i in range(len(mns))];

# A list created for holding clusters
blngsTo = [0 for i in range(len(tms))];

for e in range(mxtrtns):

# If no change of cluster occurs, halt
nChng = True;
for i in range(len(tms)):

tm = tms[i];

# Classify into cluster and update the
# corresponding means. 
ndx = Classify(mns,item);

clusterSizes[index] += 1;
cSize = clusterSizes[index];
means[index] = UpdateMean(cSize,means[index],item);

# Item changed cluster
if(index != belongsTo[i]):
noChange = False;

belongsTo[i] = index;

# Nothing changed, return
if (noChange):
break;

return means;

You can also try this code with Online Python Compiler

Run Code

Find Clusters

Finally, given the means, we wish to find the clusters. We'll go over all of the objects, classifying each one into the cluster it belongs to.

def FindClusters(mns,tms):
clusters = [[] for i in range(len(mns))]; # Init clusters

for item in items:

# Classify item into a cluster
index = Classify(means,item);

# Add item to cluster
clusters[index].append(item);

return clusters;

You can also try this code with Online Python Compiler

Run Code

The following are some more commonly used similarity measures:

1. The cosine distance determines the cos angle between the point vectors of two points in n-dimensional space.

2. Manhattan distance: The total of the absolute differences between the coordinates of the two data points is calculated.

3. The generalized distance metric is also known as the Minkowski distance. Its application is in both ordinal and quantitative variables.