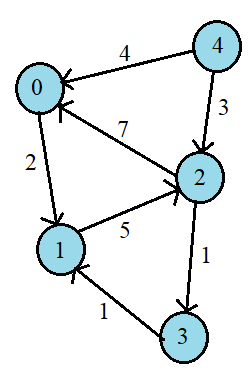
Karp’s Algorithm for Minimum Mean Weight Cycle
Karp’s algorithm gives a straightforward solution to find the cycles with a minimum average. In this algorithm, we will be using a dynamic programming approach. We will maintain a table to store the values, and the minimum of these values gives the required answer. This approach is most efficient because the problem contains several overlapping subproblems and optimal subproblems.

The algorithm of the optimized solution is given below:
-
Choose any vertex v1 as the source vertex.
-
We define a table d where each entry dK(v) is the shortest directed path to v from v1 using exactly k edges. (use infinity if no such path exists)
-
Initialize d0 to infinity for all vertices instead of v1.
-
The value of dK can be calculated recursively using the following relation:
dK(v,w) = min (dK-1(v) + weight(v,w)) for all edges(v,w)
-
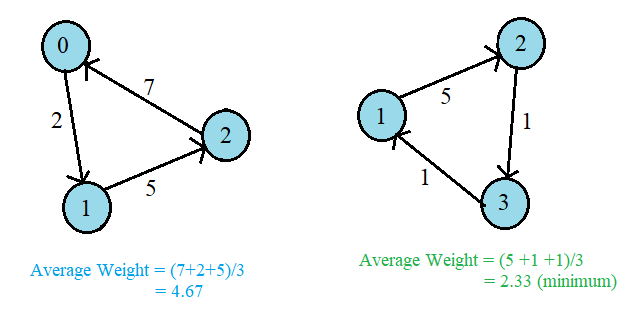
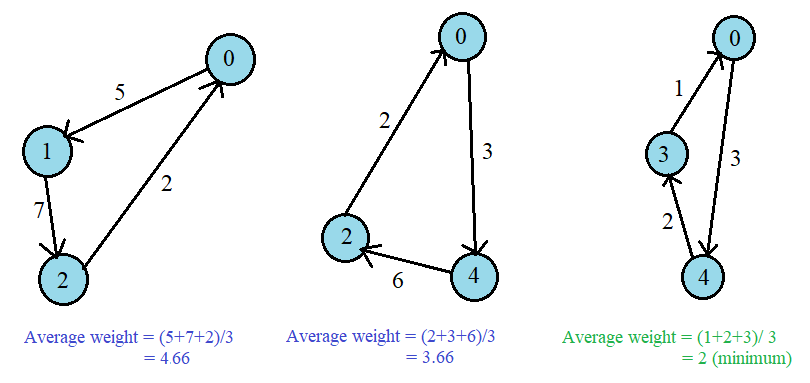
Once the table is computed, we can compute the minimum average cycle using the following relation.
Minimum average weight = max(dn(v) − dk(v)) / (n − k).
-
Finally, the minimum of all the values calculated above is the required answer.
Let us now look at the implementation of Karp’s Minimum mean weight cycle algorithm in C++ and Python.
C++ Implementation 📌
#include<bits/stdc++.h>
#include<vector>
using namespace std;
const int num_of_vertices = 5;
/* Struct variable to represent edge */
typedef struct{
int from, wt;
}edge;
/* a vector of type edge to store the edges of the given graph*/
vector <edge> edges[num_of_vertices];
/*Helper Function to add an edge in the graph */
void AddEdge(int v1 ,int v2 ,int wt)
{
/* Since the graph is directed, we have to add only the forward edge*/
edges[v2].push_back({v1, wt});
}
/* Function for Karp's Minimum average weight cycle algorithm */
double KarpsAlgo(int d[num_of_vertices+1][num_of_vertices])
{
/* An array to store average values */
vector<double> avg(num_of_vertices, -1);
/* Calculate the average of cycles using the d table */
for (int i=0; i<num_of_vertices; i++)
{
if (d[num_of_vertices][i] != -1)
{
/*calculating average using Karps Algorithm */
for (int j=0; j<num_of_vertices; j++)
if (d[j][i] != -1)
avg[i] = max(avg[i],
((double)d[num_of_vertices][i]-d[j][i])/(num_of_vertices-j));
}
}
/* Finding the minimum average value */
double ans = 100000000000;
for (int i=0; i<num_of_vertices; i++){
if (avg[i] > -1 && avg[i] < ans)
ans = avg[i];
}
return ans;
}
/* Driver Function */
int main()
{
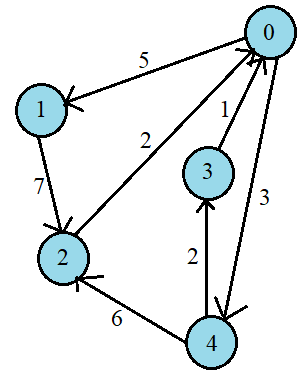
/* Adding Edges to the graph */
AddEdge(0, 1, 2);
AddEdge(1, 2, 5);
AddEdge(3, 1, 1);
AddEdge(2, 3, 1);
AddEdge(2, 0, 7);
AddEdge(4, 0, 4);
AddEdge(4, 2, 3);
/* initializing the d table to store the shortest path distance */
int d[num_of_vertices+1][num_of_vertices];
/* set all values of d as -1 */
for (int i=0; i<=num_of_vertices; i++)
for (int j=0; j<num_of_vertices; j++)
d[i][j] = -1;
d[0][0] = 0;
/* calculating the shortest path and updating the table d */
for (int i=1; i<=num_of_vertices; i++)
{
for (int j=0; j<num_of_vertices; j++)
{
for (int tmp=0; tmp<edges[j].size(); tmp++)
{
if (d[i-1][edges[j][tmp].from] != -1)
{
int curr_wt = d[i-1][edges[j][tmp].from] +
edges[j][tmp].wt;
if (d[i][j] == -1)
d[i][j] = curr_wt;
else
d[i][j] = min(d[i][j], curr_wt);
}
}
}
}
/* Calling the KarpsAlgo function with d table and printing the results*/
double ans = KarpsAlgo(d);
cout <<ans;
return 0;
}

You can also try this code with Online C++ Compiler
Python Implementation 📌
''' Class to represent an edge of the directed weighted graph'''
class edge:
def __init__(self, u, wt):
self.From = u
self.wt = wt
num_of_vertices = 5
''' To store the edges '''
edges = [[] for i in range(num_of_vertices)]
'''Helper Function to add an edge in the graph '''
def AddEdge(v1, v2, wt):
''' Since the graph is directed, we have to add only the forward edge'''
edges[v2].append(edge(v1, wt))
''' Function for Karp's Minimum average weight cycle algorithm '''
def KarpsAlgo(d):
''' An array to store average values'''
avg = [-1 for i in range(num_of_vertices)]
''' Calculate the average of cycles using the d table '''
for i in range(num_of_vertices):
if d[num_of_vertices][i] != -1:
'''calculating average using Karps Algorithm '''
for j in range(num_of_vertices):
if (d[j][i] != -1):
avg[i] = max(avg[i],(d[num_of_vertices][i]-d[j][i])/(num_of_vertices-j))
''' Finding the minimum average value '''
ans = 100000000000;
for i in range(num_of_vertices):
if (avg[i] > -1 and avg[i] < ans):
ans = avg[i]
return ans
'''Driver Function'''
def main():
''' Adding Edges to the graph'''
AddEdge(0, 1, 2)
AddEdge(1, 2, 5)
AddEdge(3, 1, 1)
AddEdge(2, 3, 1)
AddEdge(2, 0, 7)
AddEdge(4, 0, 4)
AddEdge(4, 2, 3)
''' initializing the d table to store the shortest path distance '''
d = [[None] * num_of_vertices for i in range(num_of_vertices + 1)]
for i in range(num_of_vertices + 1):
for j in range(num_of_vertices):
d[i][j] = -1
d[0][0] = 0
''' calculating the shortest path and updating the table d '''
for i in range(1, num_of_vertices+1):
for j in range(num_of_vertices):
for k in range(len(edges[j])):
if d[i-1][edges[j][k].From] != -1:
cwt = d[i-1][edges[j][k].From] + edges[j][k].wt;
if d[i][j] == -1:
d[i][j] = cwt
else:
d[i][j] = min(d[i][j], cwt)
''' Calling the KarpsAlgo function with d table and printing the results'''
ans = KarpsAlgo(d)
print(ans)
'''Executing Main'''
main()

You can also try this code with Online Python Compiler
Input
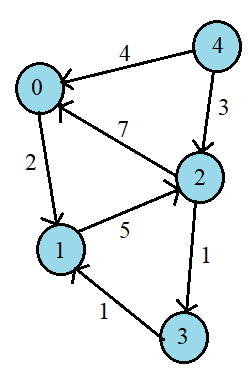
Output
2.33
Complexities 📈
Time Complexity ⏳
O(N * K), where N denotes the count of nodes in the graph and K denotes the number of edges.
Reason: The time of N*K is taken to generate table d, which holds the shortest distances.
Auxiliary Space Complexity 💾
O(N * K + N), where N denotes the count of nodes in the graph and K denotes the number of edges.
Reason: The extra space of N*K is needed for table d to store the shortest paths. Space of N is also required to store the average weights in avg vector.
Check out this problem - Minimum Coin Change Problem
Frequently Asked Questions
What is a graph?
A graph is a data structure used to represent highly correlated data. A graph is made up of vertices and edges. The edges are used to connect the vertices based on some relationship.
What is dynamic programming?
Dynamic programming is a programming methodology that optimizes simple recursions. It is beneficial in problems that contain overlapping subproblems. The idea is to store the results of previous subproblems so that they can be used in later overlapping subproblems.
What is a tree?
A Tree is a non-linear data structure similar to a graph that stores data hierarchically. A tree is an undirected graph with no cycles. Each tree has a root node and edges that connect the root node with its child nodes.
How do you represent a graph in programming?
A graph is made up of vertices and edges. There are two ways to denote the edges: adjacency list and adjacency matrix. An adjacency matrix takes more space than an adjacency list; hence, it is less preferred.
Why do we calculate the complexities of a program?
Complexities of a program are used to compare two or more approaches to solve the same problem. It provides a measure to compare and find a more efficient solution in terms of time and space.
Conclusion
This article discussed the algorithm and implementation of Karp’s Minimum Mean (or Average) Weight Cycle Algorithm. To learn more on this topic, visit Find Minimum Weight Cycle in an Undirected Graph, Design and Analysis of Algorithms.
I hope you would have gained a better understanding of these topics now!
Are you planning to ace the interviews with reputed product-based companies like Amazon, Google, Microsoft, and more?
Attempt our Online Mock Test Series on Coding Ninjas Studio now!
Happy Coding!