Kth ancestor of a node in a binary tree

Introduction

In this blog, we will get to understand a very interesting problem of a Binary Tree data structure in which backtracking has been used. Through that problem, we will learn how to approach any backtracking binary tree problem. Firstly, we will look into the problem statement, get some knowledge about Binary tree data structure, decide what will be the optimum approach, and then we will proceed towards the implementation in any of the programming languages.

What is a Binary Tree?

A Binary Tree is sort of a tree data structure in which elements have the utmost two children nodes. Since, in this data structure, elements have only two children nodes, we name them the left child and the right child.

A Binary Tree is sort of a tree data structure in which elements have the utmost two children nodes. Since, in this data structure, elements have only two children nodes, we name them the left child and the right child.

Any node of Binary contains the following information. These are:

1. Its data
2. Pointer to its left child.
3. Pointer to its right child.

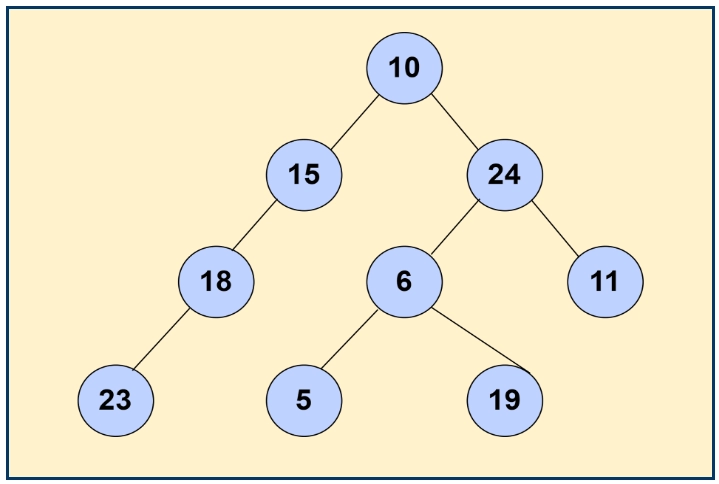
For Example, if we consider the tree above, 10 is the root node, and the rest of the nodes are its children nodes. We pick any node, say 6, so, 5 will be its left child and 19 will be its right child. That is, 6 is the parent node to children nodes 5 and 19.

Problem Statement

We are given a binary tree that has n nodes. We have to find the kth ancestor of a given node of that binary tree. When we say kth ancestor, it means the kth parent node.

Here, we are assuming that all the values inside the nodes are positive.

Sample Examples

Now, let us understand the problem with the help of an example.

Suppose that we have a binary tree as you can see in the image below. We have to search for the kth ancestor of the given node in that binary tree. We will use the same binary tree for different examples to see what will be the output in different possible cases.

Explanation

In the above example, we will search for the input ‘val’ in the binary tree, which is 8. As soon as we get the node, we will traverse above to its ‘k-th’ parent, which is the 2nd parent in this case. We observe that the 2nd parent is present and the value of the 2nd parent of 8 is 3. So, our output will be 3.

Explanation

In the above example, we will search for the input ‘val’ in the binary tree, which is 10. As soon as we get the node, we will traverse above to its ‘k-th’ parent, which is the 4th parent in this case. We observe that the 4th parent is not present. In such cases when the parent is absent, the output will be null.

Explanation

In the above example, we will search for the input ‘val’ in the binary tree, which is 6. As soon as we get the node, we will traverse above to its ‘k-th’ parent, which is the 0th parent in this case. Since the value of k is 0, no traversal will be done and the value of output will be the same as the value of input ‘val’

Approach

To solve this problem, we will use Depth First Search (DFS). Here, we are taking advantage of Backtracking to present the optimal approach to this. Once, we find the position of the given node, we will track it back to its kth ancestor to get our output using recursive functions. We will check for the conditions such as that if the kth ancestor is the node present in the tree or not if it is then, its value will be displayed. If the kth ancestor is not present in the tree, then we will output null.

PseudoCode

static treenode kthParent(int val, treenode parent)
{
   if (parent == null)
   return null;
   if ((parent.value == val) || ((obj = kthParent(val, parent.l)) != null) || ((obj = kthParent(val, parent.r)) != null)){
      if(k > 0) k--;
      else if (k == 0)
      {
        System.out.print(parent.value);
        return null;
      }
      return parent;
   }
   return null;
}

Implementation in Java

import java.util.*;
class treenode{
  int value;
  treenode l, r;
}
class Main{
  static treenode begin(int value)
  {
    treenode obj = new treenode();
    obj.value = value;
    obj.l = obj.r = null;
    return obj;
  }
  static int k;
  static treenode obj = null;
  //main function to call functions and input values
  public static void main(String[] args)
  {
    treenode parent = begin(5);
    parent.l = begin(7);
    parent.r = begin(3);
    parent.l.l = begin(9);
    parent.l.r = begin(6);
    parent.r.l = begin(1);
    parent.r.r = begin(4);
    parent.l.l.l = begin(2);
    parent.l.l.r = begin(8);
    k = 3;
    kthParent(8, parent);
  }
  //Functio to find kth ancestor 
  static treenode kthParent(int val, treenode parent)
  {
    if (parent == null)
      return null;
    //checking the required conditions
    if ((parent.value == val) || ((obj = kthParent(val, parent.l)) != null) || ((obj = kthParent(val, parent.r)) != null)){
      if(k > 0) k--;
      else if (k == 0){
        System.out.print(parent.value);
        return null;
      }
      return parent;
    }
    return null;
  }
}

Input: 

Node= 8, k=2

Output: 

7

Complexity Analysis:

Time Complexity: In the implementation above, the pointer may have to traverse all the nodes before finding the required node. Therefore, the time complexity, in this case, will be O(n).

Space Complexity: Since we are not using any extra space, the space complexity will be O(1).

Also check out - Inorder Predecessor