Absolute Difference - Naukri Code 360

Introduction

In this blog, we will try to grab hold of a single-dimensional Array data structure problem in which dynamic programming has been used. Through that problem, we will try to understand how to approach any dynamic programming array data structure problem. The examples presented will help you clear your concepts, Pseudocode will provide you with an immediate solution, and the implementation part will give you a detailed understanding of every step.

What is an Array Data Structure?

A collection of elements stored at contiguous memory locations is an Array. The elements stored in the array are of the same type. The contiguous memory locations of the array make it easier to calculate the position of each element in the array.

The first element is at index 0. As we transverse the array, the index increases by 1 till n-1 if there are n elements in the array.

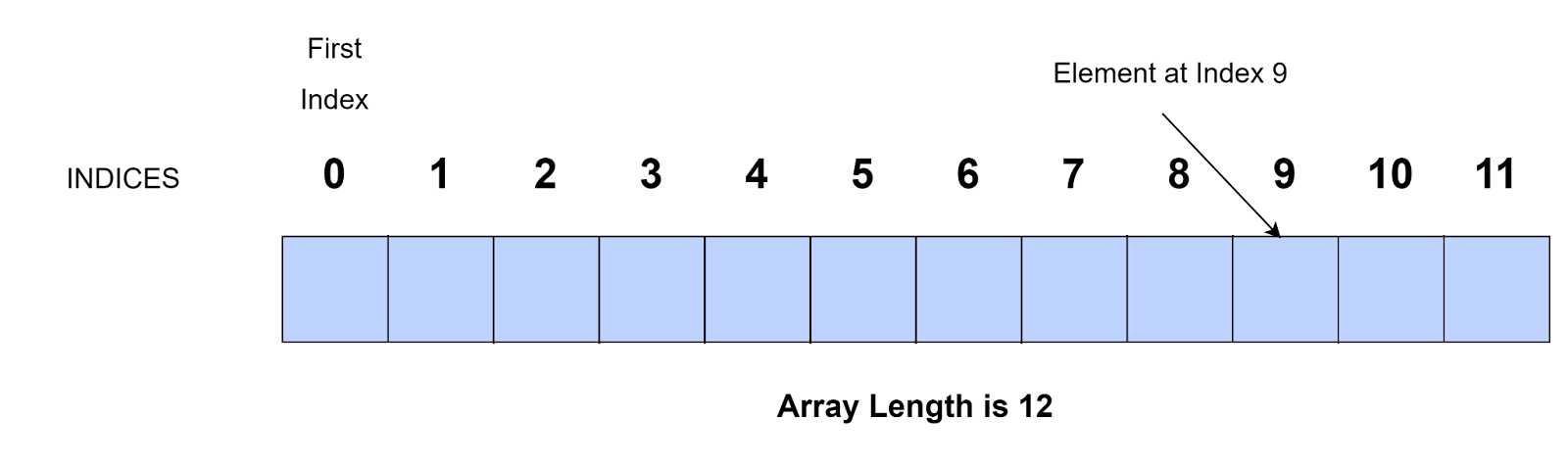
Example Array

Problem Statement

Firstly, we will have a look at what exactly the problem says.

Given an array of ‘n’ elements. We have to find the ‘kth’ smallest absolute difference of the two elements present in that array.

The absolute value of the difference between the two numbers of any pair (x, y) is defined as the absolute difference between x and y.

Here, we are assuming that all the elements in an array are positive.

Example 1:

Explanation: First, we will look into all the possible pairs that can be created from the nums[] and the absolute difference between them in the following table.

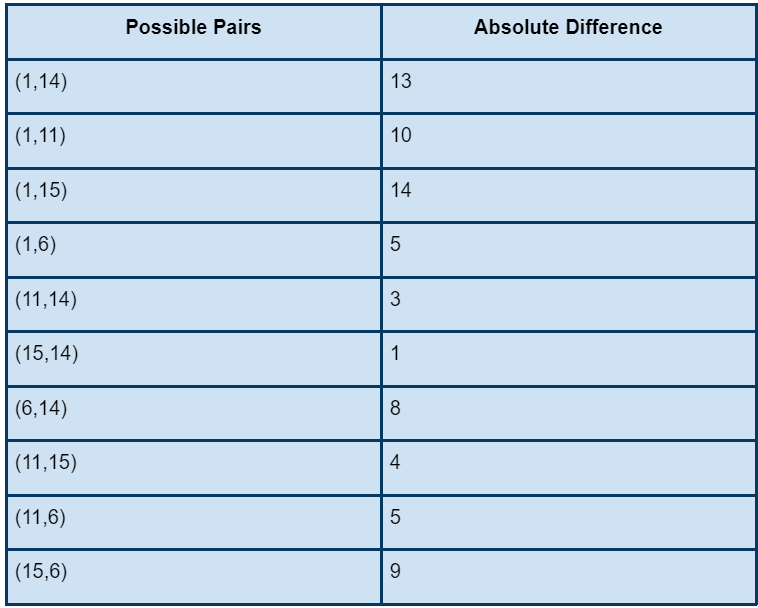
Given k for this example is 6. Now, we will determine the 6th smallest absolute difference, which is 8. So, 8 will be displayed as the output.

Example 2: For a better understanding, we will consider one more example.

First, we will look into all the possible pairs that can be created from the nums[] and the absolute difference between them in the following table.

This time we will repeat some values to see if it brings any change in the answer.

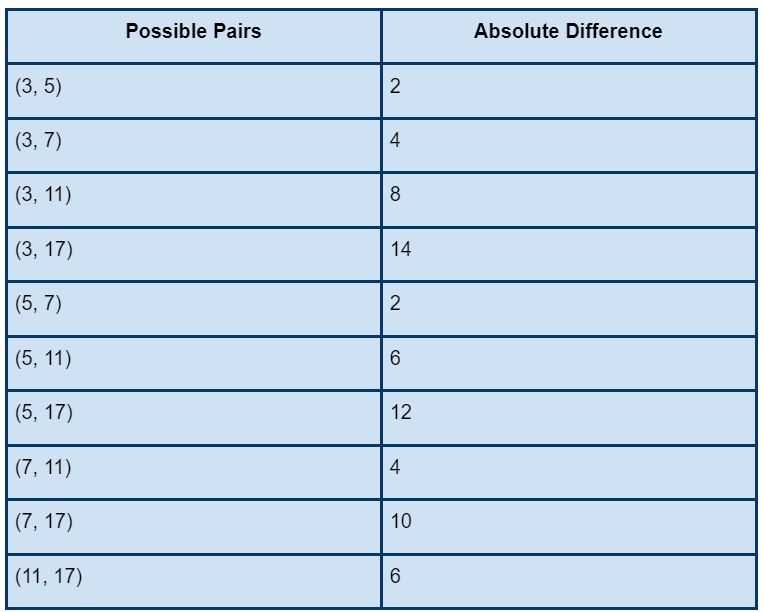
From the above table, it is clear that repeating value doesn’t bring much change. It just reduces the number of possible pairs that could have been created if there were different values.

Given k for this example is 3. Now, we will determine the 3rd smallest absolute difference, which is 4. So, 4 will be displayed as the output.

Approach

Why we don’t go for the Naive Approach?

What happens in the Naive Approach is that we will find absolute differences for all possible pairs as we saw in the example. Put them all in an array and sort the array. Then, according to the given ‘k’, we will traverse through that array and find the kth smallest absolute difference.

If we follow the Naive Approach, in that case, the time complexity will be equal to O(N^2(log(N)), which is not optimal at all. In such a situation, it is better if we go with the approach given below.

What will be the optimal approach then?

We will use Binary Search Approach. The smallest absolute difference which could ever be present will be obviously zero, in case any of the values in the array is repeated. Now, we will find the maximum absolute difference, which will be the difference between the smallest and the largest elements of the array. Clearly, we know the maximum possible difference in all possible pairs will be this. We know that our output will be between these two values, so we will go for Binary Search in this problem to solve it.

Step-1:

We will take an example array of ‘n’ elements and k=3 as input. We will sort the array.

Step-2:

Now that we have sorted the array, we will find the absolute difference of all the possible pairs. Considering the example above, the lower bound is 1 and the upper bound is 8. So, the mid-value will be 4 because the decimal is ignored. We will use the Sliding Window technique with two pointers to determine the number of pairs whose differences are less than or equal to the mid-value we calculated.

Step-4:

Based on the results of that condition, we are going to fix our search base from lower bound to mid-value or from mid-value to upper bound and continue searching.

We will have 6 such pairs and 6 is greater than 3(k). This means our 3rd smallest absolute difference obviously lies between lower bound and mid-value.

Step-5:

Now, the lower bound remains 0 but the upper bound changes to 4. So, the mid-value also changes to 2. Again, we will check for the number of pairs whose absolute difference is less than or equal to 2. We will have 3 such pairs. This means our 3rd smallest absolute difference obviously lies between lower bound and mid-value.

Step-6:

Again, the lower bound remains 0 but the upper bound changes to 2. We will come to a situation when left meets right, that is we will be left with only one value. That’s where our search will end. And, we will get 2 as the output.

Must Read Lower Bound in C++

PseudoCode

static boolean issmalldiff(int[] nums, int k, int mid)
    {
        int count = 0, left = 0;
        for(int right = 1; right< nums.length; right++)
        {
            while(nums[right] - nums[left]> mid)
            {
                left++;
            }
            count += right-left;
        }
        return(count >= k);
    }

Implementation in Java

import java.util.*;
import java.lang.*;
import java.io.*;
public class Main
{
    //function to possible absolute differences
    static boolean issmalldiff(int[] nums, int k, int mid)
    {
        int count = 0, left = 0;
        for(int right = 1; right< nums.length; right++)
        {
            while(nums[right] - nums[left]> mid)
            {
                left++;
            }
            count += right-left;
        }
        return(count >= k);
    }
    //function to get k-th smallest difference
    public static void main(String[] args)
    {
        int nums[] = {10,13,7,5,11};
        int k= 4;
        Arrays.sort(nums);
        int left = 0;
        int right = nums[nums.length-1] - nums[0];
        while(left<right)
        {
            int mid= (left+right)/2;
            if(issmalldiff(nums,k,mid))
                right = mid;
            else
                left = mid+1;
        }
        System.out.println(left);
    }
}

Input

nums = {10, 13, 7, 5, 11}, k= 4

Output

Complexity Analysis

Time Complexity

Here, we can that there is a nested loop, that is one loop inside another the outer loop is going from 1 to n and in the worst case the inner loop will also traverse from 1 to n therefore the time complexity would be O(n*n) i.e., O(n^2)

Space Complexity

Since we have not used any extra space. Thus, the space complexity for the above-given code will be O(1).

Frequently Asked Questions

How do you declare an array in Java whose size is to be input by the user?

The syntax to declare an array in Java is:

int arr = new int[n];

Here, n is the input entered by the user. The above will not only declare an array but also allocate memory to it.

What is that one characteristic of an array that comes under its advantage and disadvantage both?

One characteristic of the array is its Static nature.

The static nature of the array is very useful in the case of simple programs but when we talk about dynamic programs or certain high-level programs, then this static nature creates an issue because it leads to memory wastage.

Mention some prominent terms to describe how Array is different from ArrayList in Java.

The array is static, while ArrayList is dynamic.
The array is not resizeable, but ArrayList is.
The size of an array should be declared at the time of initialization, while in the case of ArrayList, it is not compulsory.
The array can be single or multi-dimensional, but an ArrayList is always single-dimensional.

Conclusion

In the article, we have discussed a famous problem on the array which is to find the kth smallest absolute difference of two elements in the array. We have discussed the problem statement with the help of sample examples and we have also seen the optimal solution to this problem, and in the end, we have discussed the complexities of that optimal solution

We hope the above discussion helped you understand and solve the problem better.

If you want to practice problems on array then you can refer to these links:

kth smallest absolute difference of two elements in an array