Lagrange’s Mean Value Theorem

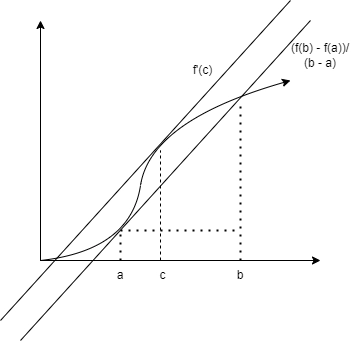
Understanding Lagrange’s Mean Value Theorem with examples

We’ll verify this theorem for an example function, f(x) = x2.- 4x + 3, here a = 1, b = 3.

=> (f(b)-f(a))/(b-a)) will be equal to (0-0)/(3-1)

=> 0

=> By Lagrange’s theorem we claim that there exists a c in the closed interval [a, b]

=> f’(c) = 0 -(1)

=> f’(x) = 2x - 4 -(2)

=> f’(c) = 2c - 4 substituting x with c

=> 2c - 4 = 0

=> c = 2

In the above solution, c = 2 lies within the closed interval [1, 3], and hence we have verified Lagrange's mean value theorem (only for this specific case), which is, however, no proof for the theorem but to give you perspective on how it can be used.

We start with a real application type problem to give you some understanding. 

Let's say that you are a software developer designing a system where you have the entry time and exit time of vehicles onto an expressway.

The information is stored as a tuple of the License plate number, Entry time and Exit time. You know that the speed limit for the vehicles is 50 Km/hr on the expressway and the length is about 100 Km.

Using the information given above, determine if you need to penalize the vehicle for exceeding the speed limits.

To understand the above question, we'll explore an example and formulate a solution by understanding it.

TripInfo = (‘XY32 FM1729‘, ‘2020-12-19 12:00:00’, ‘2020-12-19 13:30:00’)

The total time taken for the journey = 1 hour 30 minutes = 1.5 hours

The total distance travelled = 100 Km

The average speed of the vehicle during the journey = (Total distance travelled) / (Total time taken)

The average time taken = 100 / 1.5 ≈ 66.67 Km/hr

In this scenario, the rule violations are visible as we can conclude by Lagrange's Mean Value Theorem that the vehicle's speed must have been approximately 66.67 Km/hr during some point in the journey in the closed time interval mentioned above.

The vehicle's distance-time graph will be continuous and derivable for all real-world vehicles.

LMVT (Lagrange's Mean Value Theorem) is one of the theorems with multiple applications, such as finding roots of a function within an interval and helping prove equations as well as inequalities.

FAQs

1. What is Rolle’s Theorem?
Rolle’s Theorem is a special case of the LMVT (Lagrange’s Mean Value Theorem) It states that if there are two unique points where the function attains equal value, i.e., f(x) = f(y) (x != y), then there exists a point between those two points where the derivative of the function is 0 (the function must be continuous in [x, y] and derivable in (x, y)).

2. What is meant by “continuous over a closed interval” in reference to a function?
A function is said to be continuous over a closed interval [a, b] if it’s continuous 
at every point in the open interval (a, b) and continuous from right at point a and continuous from the left of b.

3. What is meant by “derivable over an open interval” in reference to a function?
A function is said to be derivable over an open interval (a, b) if it’s derivable 
at every point in the open interval (a, b). It’s handy to remember that if the function is discontinuous at some point x, then it’s also not differentiable at x.

4. How can this topic help me?
This topic is a stepping stone for proving and understanding many complicated ideas in calculus. It’s also essential as one can always expect there to be a question from this topic, as has been the case in competitive examinations like GATE, etc.

5. How to find the derivative of a function?
To find the derivative of a function, following the traditional method and finding the limit, lim_h->0 (f(x + h) - f(x)) / h = f’(x) is not always practical from a time perspective. Here, keeping some standard derivatives at hand and using the chain rule can help us find the derivative of virtually every function. Chain rule can be described as follows, (f(g(x)))’ = f’(g(x)) * g’(x).

Key Takeaways

In this article, we have extensively discussed Lagrange’s Mean Value Theorem, the conditions required for it to hold along its applications. Refer here to learn more about concepts and theorems related to mathematics.

We hope that this blog has helped you enhance your knowledge regarding Lagrange’s Mean Value Theorem and if you would like to learn more, check out some of our articles on engineering mathematics such as mathematical induction, Initial Value Theorem, set theory, inverse Laplace transforms and many more.

Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. 

Enrol in our courses and refer to the mock test and problems available.

Take a look at the interview experiences and interview bundle for placement preparations.

Do upvote our blog to help other ninjas grow. 

Happy Coding!