Introduction
You are given a Binary Tree, and you need to return the size of the largest subtree of the given Binary Tree, which is a BST(Binary Search Tree). If, in any case, your entire Binary Tree is the BST, return the size of the whole Binary Tree.
Let us see a few examples:
INPUT:
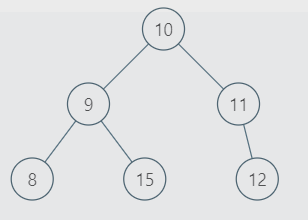
OUTPUT: 3
EXPLANATION:
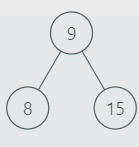
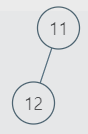



These are the only SubTrees that are BSTs. So, the largest BST subtree among them has size 3. Hence, the output is 3.
INPUT:
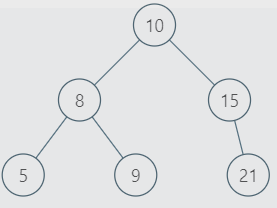
OUTPUT: 6
EXPLANATION: Since the entire Binary Tree is the BST. Hence, the largest BST Subtree is of size 6.
Approach 1
You can run any(inorder, preorder, postorder) traversal on the tree and check if the subtree rooted at your current node is BST or not. In this way, you can find the largest BST subtree size.
Please refer to the below code for the approach mentioned above.
int largestBST(Node root)
{
if (root == null){
return 0;
}
/*
calling isBST function to check if subtree
rooted at the current node is a BST or not
*/
if (isBST(root, Integer.MIN_VALUE, Integer.MAX_VALUE)){
/*
calling size function to find the size
of the subtree rooted at the current node
*/
return size(root);
}
// return the largest BST subtree size.
return Math.max(largestBST(root.left), largestBST(root.right));
}
boolean isBST(Node root, int min, int max){
if(root == null) {
return true;
}
boolean left = isBST(root.left, min, Math.min(max, root.data));
boolean right = isBST(root.right, Math.max(min, root.data), max);
/*
If left part or right part
is not BST return false
*/
if(left == false || right == false) {
return false;
}
/*
If the current node doesn't follow the BST
Property returns false.
*/
if(root.data <= min || root.data >= max) {
return false;
}
return true;
}
static int size(Node root){
if(root == null) {
return 0;
}
return 1 + size(root.left) + size(root.right);
}
Time Complexity: The time complexity for the above code is O(N ^ 2) (where ‘N’ denotes the number of nodes in the given binary tree) because, for each node, we check if the subtree rooted at the current node is BST. We call this function for each node, and ‘isBST()’ runs in O(N) time. Hence, the time complexity is O(N * N). Also time complexity of size() function is O(N).
Space Complexity: We are not using any auxiliary space, but we are using the recursive call stack space of O(N).





