Leaders in an Array

Brute Force Approach

The brute force solution to this leader in an array problem is to use nested loops to check all the elements one by one. The outer loop will help to traverse from 0 to N - 1, and the inner loop will help to check all the rightmost elements of that respective element. If the condition for being a leader is satisfied, then we’ll print that element.

Algorithm

Step 1. Create the function ‘getResult’, it will accept 2 parameters, first one will be the input array, and the second one will be the size of the array ‘N’.

Step 2. Make an iteration using the ‘for’ loop with variable ‘i’ from 0 to the size of the array, in which the inner ‘for’ loop will iterate from i + 1 to the size of the array.

Step 3. Break the loop if we find any element greater than the element on the ith position of the array, on the right side of that respective element.

Step 4. Now, if the value of ‘j’ is equal to the size of the array, this depicts that the element on the ith position is the leader element, and hence we’ll print that leader element.

Java Implementation

public class solution
{
       public static void getResult(int arr[], int N)
       {
              for (int i = 0; i < N; i++)
              {
                     int j;
                     for (j = i + 1; j < N; j++)
                     {
                            if (arr[i] <=arr[j])
                          {
                                   break;
                          }
                     }
                    
                    // The loop didn't break
                     if (j == N)
                   {
                            System.out.print(arr[i] + " ");
                   }
              }
       }

       public static void main(String[] args)
       {
              solution res = new solution();
              int arr[] = new int[]{15, 37, 1, 32, 135, 2};
              int n = arr.length;
             System.out.print(“Input :-”);
             for(int i = 0 ; i < n ; i++)
             {
                   System.out.print(arr[i] + “, “);
             }
             System.out.print(“Output :-”);

              res.getResult(arr, n);
       }
}

 

Output :
Input :- 15, 37, 1, 32, 135, 2
Output :- 2, 135

C++ Implementation

#include <stdio.h>
void leader(int a[], int n)
{
   for (int i = 0; i < n; i++)
   {
       for (int j = i; j < n; j++)
       {
           if (a[i] < a[j])
           {
               break;
           }
           if (j == n - 1)
               printf("%d ", a[i]);
       }
   }
}
int main()
{
   int a[] = { 8,3,9,1,5,0,1 };
   int n = sizeof(a) / sizeof(a[0]);
   
   leader(a, n);
}

Output:

1 5 9

Algorithm Complexity of Leaders in array problem

Time Complexity: O(N ^ 2 )

As we are using the nested loop to check for all the rightmost elements for that particular element of the array, therefore,

the overall time complexity will be O(N ^ 2)

Space Complexity: O(1)

As we are using constant space. Therefore the overall space complexity will be O(1).

Check out this problem - First And Last Occurrences Of X

Efficient Approach

If we look closely at the above approach, we will notice that we are checking all the rightmost elements for one particular element of that array, but we can optimize it by starting the iteration from the right side and keeping the track of the maximum array till that particular element of the array. We need to print the element when maximum changes its value.

Algorithm 

Step 1. Create a function ‘getResult()’ that will accept the 2 parameters, the first one is the input array, and the second one is the size of that array.

Step 2. Initialize a variable ‘max_till’ with the rightmost element of the array.

Step 3. Make an iteration using the ‘for’ loop with variable ‘i’ from the second last element of the array to the first element of the array.

Step 4. Change the value of ‘max_till’ if the value of the ith element of the array is greater than ‘max_till’. 

Step 5. Print the value of ‘max_till’

Java Implementation

public class LeadersInArray
{
       pubic static void getResult(int arr[], int N)
       {
              int max_till = arr[N - 1];

              /* Rightmost element is always leader
              System.out.print(max_till + " ");

              for (int i = N - 2; i >= 0; i--)
              {
                     if (max_till < arr[I])
                     { 
                           max_till = arr[I];
                           System.out.print(", " + max_till + " ,");
                     }
              }
       }

       public static void main(String[] args)
       {
              solution res = new solution();
              int arr[] = new int[]{15, 37, 1, 32, 135, 2};
              int n = arr.length;
              res.printLeaders(arr, n);
       }
}

Output :

Input :- 15, 37, 1, 32, 135, 2
Output :- 2, 135

C++ Implementation

#include <stdio.h>
void leader(int a[], int q)
{
   int p = a[q - 1];
   printf("%d ", p);
   for (int i = q - 2; i >= 0; i--)
   {
       if (a[i] > p)
       {
           p = a[i];
           printf("%d ", p);
       }
   }
}
int main()
{
   int a[] = { 8,3,9,1,5,0,1 };
   int q = sizeof(a) / sizeof(a[0]);
   leader(a, q);
}

Output:

1 5 9

Python Implementation

def leader(a, q):
   p = a[q-1];
   print(p, " ")
   for i in range(q-2, -1, -1):
       if (a[i] > p):
           p = a[i];
           print(p, " ")
           
a = [ 8,3,9,1,5,0,1 ]
q = len(a)
leader(a, q)

Output:

1 5 9

Algorithm Complexity of Leaders in array problem

Time Complexity: O(N)

As we are traversing the complete array once from the right side, therefore, the overall time complexity will be O(N).

Space Complexity: O(1)

As we are using constant space, therefore, the overall space complexity is O(1).

To learn about Fibonacci Series in Python check this out.

Frequently asked questions

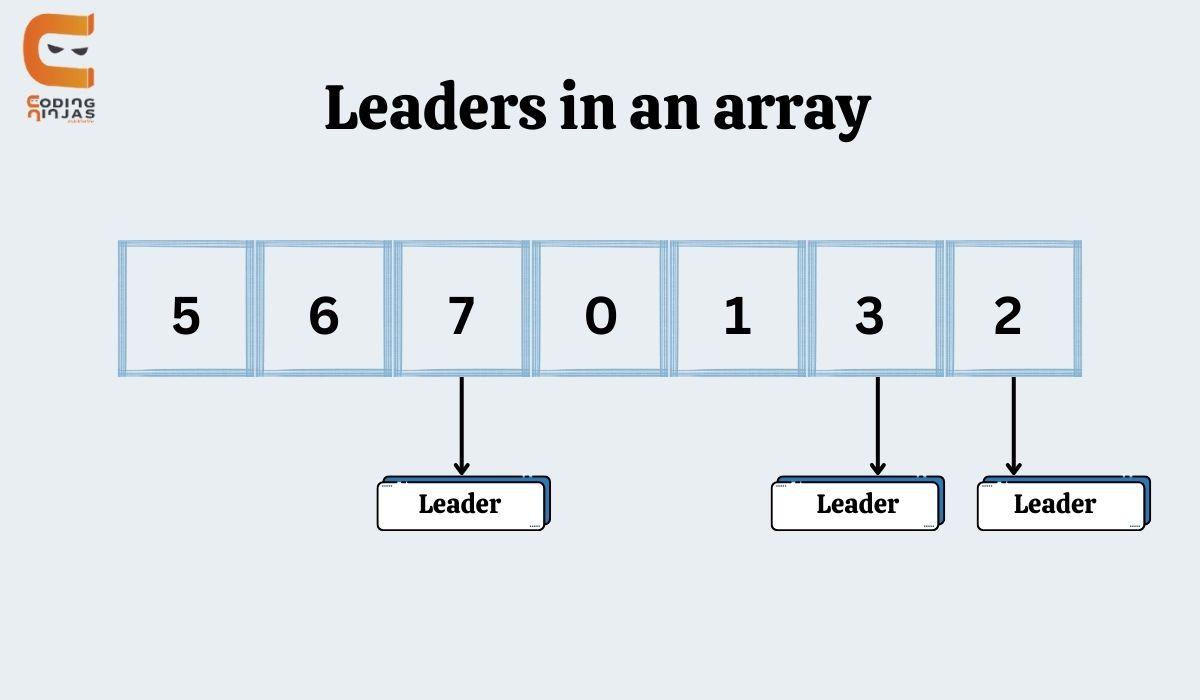
What is a leader in an array?

If an element is bigger than every other element to its right, it is considered a leader. And the last element is always the leader element. It can be obtained with the help of two loops.

What are examples of leaders in array?

Input: a[] = {15, 16, 4, 3, 2}, Output: 16, 2
Input: a[] = {1, 2, 3, 4, 5, 2}, Output: 5, 2.

What is the greatest leader in an array?

A leader in an array is the element of the array that is greatest compared to all the elements residing on the right side of that element. According to this, the rightmost element will always be the leader.

How do you find the leader element in an array?

Using two loops, we can get the leader element. The outermost loop goes from 0 to size–1 and selects each element one at a time from left to right. The selected element is compared to every element on its right side by the inner loop. The chosen element is the leader if it is larger than all of the elements to its right. 

Conclusion

In this article, we discussed What is Leaders in the array, discussed the various approaches to solve this problem programmatically, and discussed the time and space complexities. Later, we find out different ways to reduce time complexity. If you want to practice more problems, then you can visit Coding Ninjas Studio.

Also read, Array in Javascript

Read more: Array in Java

If you think that this blog helped you, then share it with your friends!. Refer to the DSA C++ course for more information.

Until then, All the best for your future endeavors, and Keep Coding.