Leading and Trailing in Compiler Design

What is Leading and Trailing in Compiler Design?

LEADING

LEADING is defined for each non-terminal. Every non-terminal is defined such that terminals can be the first terminal in a chain derived from this non-terminal.

The function LEADING is defined as follows:

LEADING(A) = { a| A ⇒+ γaδ, where γ is ∊ or one non-terminal., 

• where => denotes derivation,
   
• . + indicates one or more steps.
   
•  And A is non-terminal.
   

 Thus, LEADING(A) can be interpreted as finding the first terminal from the left in the RHS of production using all possible derivations for production.

Algorithm for Leading

LEADING(A)

{

1. ‘a’ is in Leading(A) if A →γaδ where γ is ε or any Non-Terminal.
    
2. If’ ‘a’ is in Leading(B) and A →B, then ‘a’ in Leading(A).

}

Step 1: This algorithm shows us how to add the first terminal occurring in the RHS of each production directly.”

Step 2: This algorithm suggests adding the first terminal over the next.

Non-terminal B will be included indirectly in the LEADING() of each non-terminal.

TRAILING

TRAILING for each non-terminal are those terminals that may be the last terminals in the chain or string derived from that NT.

The function TRAILING is defined as follows:

TRAILING(A) = { a| A ⇒ + γaδ, where δ is ∊ or one non-terminal., 

• Where => denotes a derivation.
   
• + denotes in one or more steps.
   
• A is non-terminal. 
   

Thus, TRAILING(A) can be interpreted as finding the first terminal from the right in the RHS of the production using all possible derivations for the production.

Algorithm for TRAILING

TRAILING (A)

{

1. ‘a’ is in Trailing(A) if A→γaδ, where δ is ε or any non-terminal
 

2. If ‘a’ is in Trailing(B) and A→B, then ‘a’ is in Trailing(A)

}

This algorithm is much like the LEADING algorithm. The only distinction is that the symbol is looked at from right to left in preference.

Step 1: The first step of this algorithm refers to finding the first terminal occurring in the RHS of the production from the right side and thus adding the direct first symbol.

Step 2: The second step looks to add the indirect first symbol to the right from the RHS of the production.

Example: Consider the unambiguous version of the expression grammar

1. E ->E + T

2. E ->T

3. T ->T * F

4. T ->F

5. F  ->(E)

6. F ->id

Solution:

Consider productions F from productions 5 and 6. There is only one symbol from production 6 on the RHS, and that is a terminal. So "id" will be in LEADING(F). From production 5, the first symbol itself is a terminal "(" and, therefore, will also be added to LEADING(F). Further additions to LEADING(F) are not possible as the first symbol on the right-hand side of the production involving F is terminal. So,

LEADING (F) = {( , id}

Consider the production T defined by productions 3 and 4. From production 3, the first symbol on the RHS is a non-terminal symbol, and the first terminal is '*', so '*' will be in LEADING(T). Then by production 4, there is only one symbol on the RHS, and that is a non-terminal symbol. Therefore, LEADING of RHS non-terminals also exists for LHS non-terminals. Therefore, LEADING(T) includes LEADING(F) in addition to "*".

LEADING (T) = { *, (, id }

A similar analogy, as explained for non-terminal T, is used to define LEADING(E). So LEADING(E) will include LEADING(T) from production 2 and "+" from production 1. So,

LEADING (E) = { + , * , ( , id}

Consider the calculation of TRAILING (), which is similar to LEADING (), but productions are scanned from right to left. Let's start again from F. From production 6, "id"  will be in TRAILING(F) because it is the only symbol in the RHS. Additionally, from production 5, ")" will be in TRAILING(F) and will have no other symbols because the first symbol from the right is terminal in both productions.

TRAILING (F) = {), id}

Similarly, from productions 3, and 4, TRAILING(T) would contain "*" and TRAILING(F) from both productions. Thus,TRAILING (T) = { *, ), id}

TRAILING (T) = { *, ), id}

Similarly, from production 1,2, TRAILING(E) would contain "+" and TRAILING(T) from these two productions. Thus,

TRAILING (E) = { +, *, ), id}

Also check out - Phases of Compiler

Importance of Leading and Trailing in Parsing

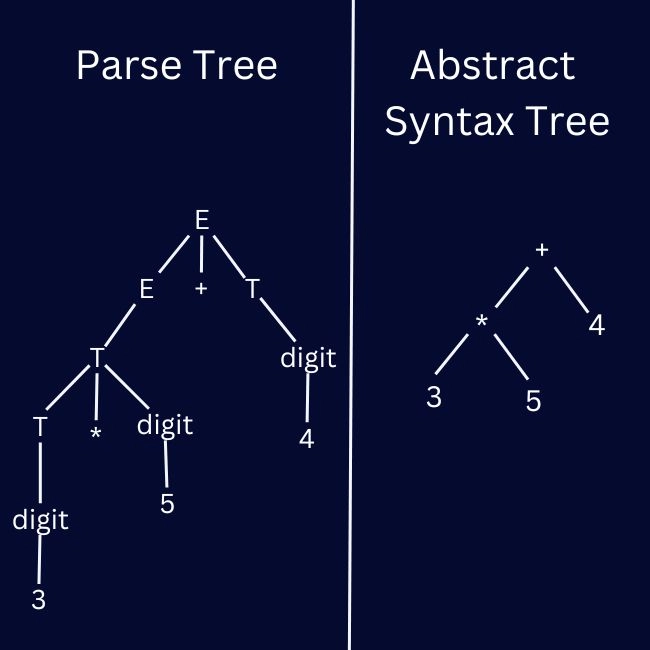
In programming, there are certain terms that shouldn't be forgotten. One example is Leading and Trailing in Compiler Design. This pair holds weight because together, they shape how parse trees come into being: detailed maps showcasing syntax structures where nodes portray non-terminals while leaves depict terminals. With this in hand, much can then be accomplished, such as fine-tuning details and forming clear code.

The construction of a parse tree involves applying the production rules of the grammar to the input tokens. For each non-terminal in the production rule, the parser must determine the set of terminals that can appear immediately before and after the non-terminal. This is where leading and trailing come into play. The parser uses the leading and trailing sets to decide which production rule to apply and how to construct the parse tree.

Must Read Recursive Descent Parser.

Frequently Asked Questions

Can leading and trailing sets be empty?

Yes, it is feasible for Leading and Trailing sets to be empty. This can occur when a non-terminal has no production rule that starts off or ends with a terminal symbol.

Are leading and trailing sets unique for every non-terminal symbol?

Yes, leading and trailing units are unique for each non-terminal symbol. Each non-terminal symbol has its own set of leading and trailing terminals, which are determined by the production rules for that symbol.

What are some commonplace uses of Leading and Trailing in Compiler Design?

Leading and trailing sets are used in many factors of compiler layout, along with lexical analysis, syntax evaluation, and semantic evaluation. They are used to construct predictive parsing tables, discover conflicts inside the parsing process,  generate intermediate code, and optimize code.

How are leading and trailing units computed in practice?

They are regularly computed with the use of algorithms that traverse the production rules for every non-terminal symbol in a grammar, including the recursive descent parser.

Conclusion

Leading and Trailing are really important in Compiler Design. These two play an important role in creating a parse tree. They help in finding the first and last terminals and non-terminals. Parser easily determines which production rules to apply by using these defining features prepared by their leadings/trailings. Later on, we can generate a parse tree from this.

To learn about operator precedence, you can visit our blog. To learn about compiler design, you can visit our blog. To learn about the Introduction to compilers, you can visit our blog.
For more information, refer to our Guided Path on Coding Ninjas Studio to upskill yourself in Python, Data Structures and Algorithms, Competitive Programming, System Design, and many more! Head over to our practice platform, Coding Ninjas Studio, to practice top problems, attempt mock tests, read interview experiences and interview bundles, follow guided paths for placement preparations, and much more! Nevertheless, consider our paid courses to give your career an edge over others!

Do upvote our blogs if you find them helpful and engaging!

Happy Learning!