Length of a Linked List(Iterative and Recursive method)

Introduction

Data elements are stored dynamically in a linked list as a linear data structure.

A node represents those data elements, and a link or pointer connects them.

There are two fields in each node:

The data is contained in a linked list.
An address for the node after it.

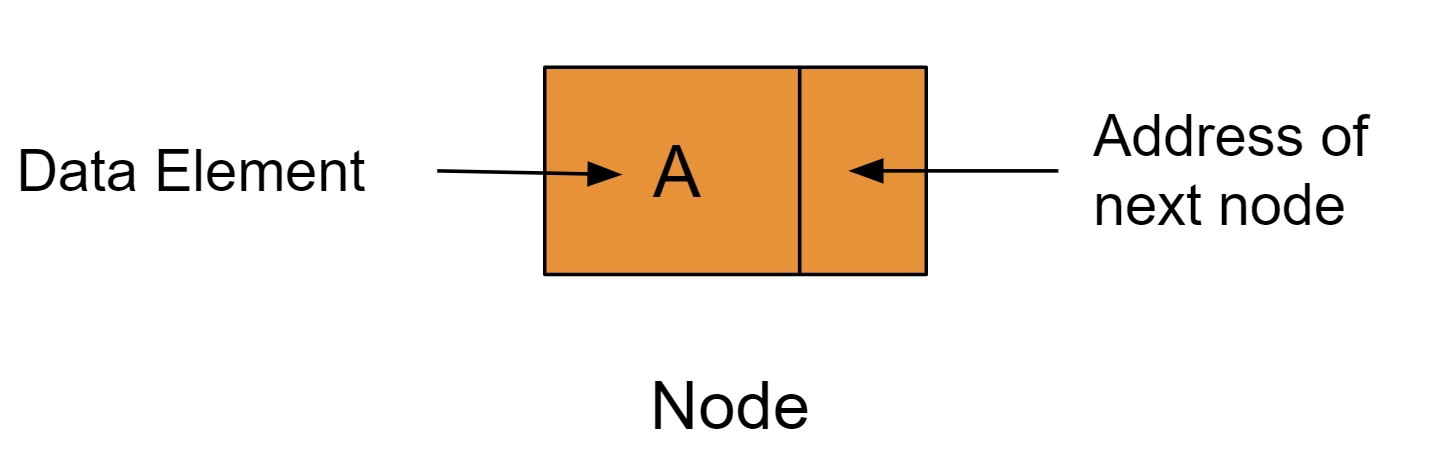
Fig: 1.1

The size of a linked list can be modified according to the requirements. There is a null in the second field of the last node since it does not point to anything.

Fig: 1.2

Problem Statement

Let's move on to the main problem we need to solve in this blog: we're given a linked list comprised of n nodes. What we need to do now is determine the length of the linked list.

Sample Example

Input:

In Fig 1.2, we have a LinkedList Stack,

Linked List: A => B => C => D

Output:

The LinkedList in Fig. 1.2 has a length of 4 because it has four linked nodes.

Approach 1: Iterative approach

Iterating continuously until a certain condition is met typically involves repeating a certain number of steps. Depending on the issue, the iterations can be large or small. All of this depends on the program we are using to iterate.

The data elements in the linked list below are in the order A => B => C => D.

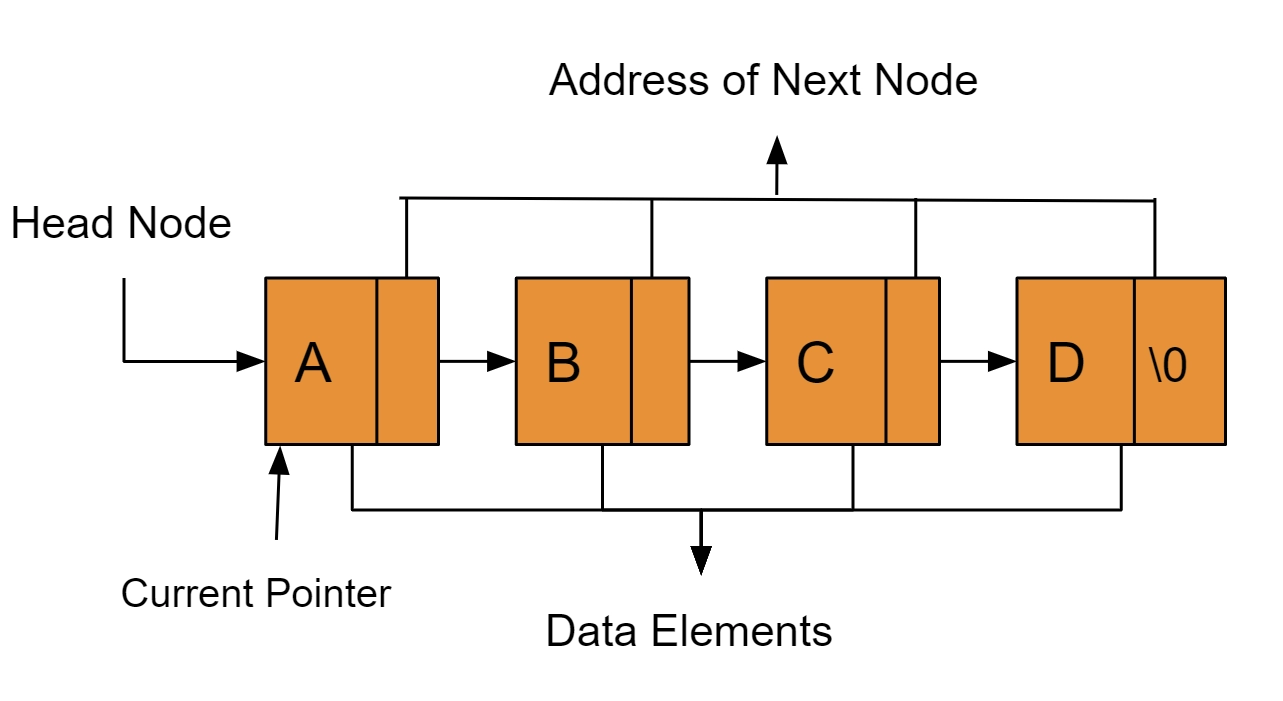
Fig 1.3

As you can see, the currentPointer is at Node A, so when it enters the while loop, it will check if the current node is null. If not, the length gets increased by one, while the currentPoniter.next points to B. If the current node is not null, the loop will continue to work, and the length will increase by one until the current node is null.

Steps of algorithm

Step-1: Initialize the pointer's current position as "currentPointer = head".

Step-2: Initialize the length of nodes as "length=0".

Step-3: Enter the while loop and perform the following operations if the current node is not empty:

length = length+1

currentPointer= currentPointer.next

Step-4: Return the length.

Implementation

Java program to calculate the length of the given Linked List.

Code in Java

// Node for LinkedList
class Node
{
    String data;
    Node next;
    Node(String d){ 
        data = d;  
        next = null; 
    }
}
// class for creating a LinkedList
class LinkedList
{
    Node head;  // head of LinkedList
    // Function to add data at the end of the LinkedList
    public void add(String val)
    {
        // adding the data to new_node
        Node new_node = new Node(val);
        // initializing the next node as head node  
        new_node.next = head;
        // Now head node is equal to the new_node  
        head = new_node;
    }
    public static void main(String[] args)
    {
        LinkedList element = new LinkedList();
        // adding elements in the LinkedList
        element.add("A");
        element.add("B");
        element.add("C");
        element.add("D");
        System.out.println("Length of the LinkedList: " +  element.getLength());
    } 
    // returns the length of the Linked List
    public int getLength()
    {
        Node currentPointer = head;
        int length = 0;
        while (currentPointer != null)
        {
            length++;
            currentPointer = currentPointer.next;
        }
        return length;
    }
}

You can also try this code with Online Java Compiler

Run Code

C++ program to calculate the length of the given Linked List.

Code in C++

#include <bits/stdc++.h> 
using namespace std; 
// Node for Linked List
class Node  
{  
    public:
    const char* data;  
    Node* next;  
};    
// class for creating a LinkedList
void add(Node** head_ref, const char* val)  
{  
    // allocating new_node
    Node* new_node =new Node(); 
    new_node->data = val;  
    new_node->next = (*head_ref);  
    (*head_ref) = new_node;  
}  
// returns the length of the Linked List
int getLength(Node* head)  
{  
    Node* currentPointer = head;
    int length = 0; 
    while (currentPointer != NULL)  
    {  
        length++;  
        currentPointer = currentPointer->next;  
    }  
    return length;  
}  
// Main function
int main()  
{
    Node* head = NULL;  
    // adding elements in the LinkedList
    add(&head, "A");  
    add(&head, "B");  
    add(&head, "C");  
    add(&head, "D");   
    // Printing the length of the LinkedList by calling the getLength()
    cout<<"Length of LinkedList: "<< getLength(head);  
    return 0;  
}

You can also try this code with Online C++ Compiler

Run Code

Output:

Length of the LinkedList: 4

Complexity Analysis

Time Complexity: The linked list is traversed once, so the time complexity is O(n).

Space Complexity: We're not using any extra space, so space complexity is O(1).

Approach 2: Recursive approach

A recursive algorithm calls itself bypassing its return value as a parameter to the next algorithm. The parameter is input, while the return value is output.

The data elements in the linked list below are in the order A => B => C => D.

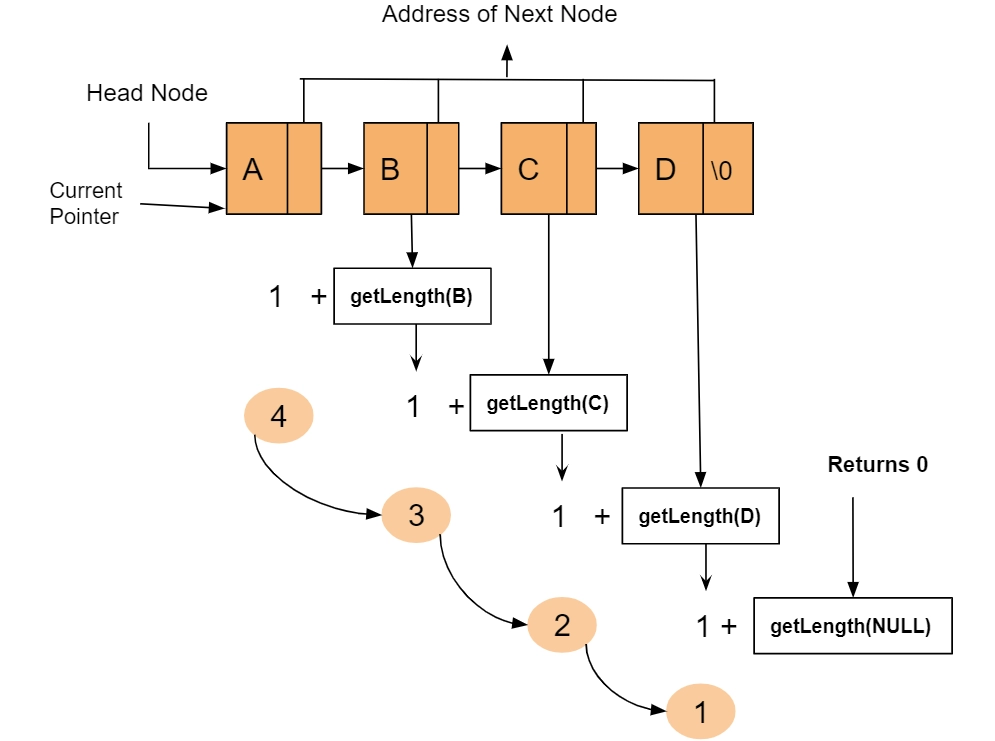
Fig 1.4

As you can see, the currentPointer is at the head of Node A, so as it enters the while loop, it will check to see if the current node is null. If not, one will be added to the block containing the getLength() element, so the loop will continue until the next node is null. As a result, if the next node is null, it will go backward, adding 1 to every value.

Algorithm

Step-1: For the base case, In getLength(head), if the head == NULL, return 0.

Step-2: Else recursively call the same Function for CurrentPointer. Next, add 1 to its result.

Step-3: Return the length.

Implementation

Java program to calculate the length of the given Linked List.

Code in Java

// Node for LinkedList
class Node
{
    String data;
    Node next;
    Node(String d){ 
        data = d;  
        next = null; 
    }
}
// class for LinkedList
class LinkedList
{
    Node head;  // head of Linkedlist
    // Function to add data at the end of the LinkedList
    public void add(String val)
    {
        // adding the data to new_node
        Node new_node = new Node(val);
        // initializing the next node as head node  
        new_node.next = head;
        // Now head node is equal to the new_node  
        head = new_node;
    }
    public static void main(String[] args)
    {
        LinkedList element = new LinkedList();
        // adding elements in the LinkedList
        element.add("A");
        element.add("B");
        element.add("C");
        element.add("D");
        //  Printing the length of LinkedList by calling the getLength()
        System.out.println("Length of the LinkedList: " +  element.getLength());
    } 
    // function to call the getCount()  
    public int getLength (){
        return getCount(this.head);
    }
    // function to call the getCount()  
    private int getCount(Node currentPointer) {
        if (currentPointer == null) {
            return 0;
        }
        return 1 + getCount(currentPointer.next);
    }
}

You can also try this code with Online Java Compiler

Run Code

C++ program to calculate the length of the given Linked List.

Code in C++

#include <bits/stdc++.h> 
using namespace std; 
// Node for Linked List
class Node  
{  
    public:
    const char* data;  
    Node* next;  
};  
// class for creating a LinkedList
void add(Node** head_ref, const char* val)  
{  
    // allocating new_node
    Node* new_node =new Node(); 
    new_node->data = val;  
    new_node->next = (*head_ref);  
    (*head_ref) = new_node;  
}  
// Recursive function to calculate the length
int getLength(struct Node* head) 
{ 
    // Base case 
    if (head == NULL) 
        return 0; 
    else
        return 1 + getLength(head->next); 
} 
// Main function
int main()  
{
    Node* head = NULL;  
    // adding elements in the LinkedList
    add(&head, "A");  
    add(&head, "B");  
    add(&head, "C");  
    add(&head, "D");   
    // Printing the length of the LinkedList by calling the getLength()
    cout<<"Length of LinkedList: "<< getLength(head);  
    return 0;  
}

You can also try this code with Online C++ Compiler

Run Code

Output:

Length of the LinkedList: 4

Complexity Analysis

Time Complexity: The traversal of the linked list is O(n) since the list is traversed only once.

Space Complexity: Due to the recursive nature of the function call stack, the space complexity is O(n).

Frequently Asked Questions

How big is a LinkedList in Java by default?

LinkedList only constructs an empty list without any initial capacity while generating a list with ten capacities by default.

Does LinkedList contain contiguous links?

A LinkedList is a linear data structure that contains objects at each node. LinkedList is not a contiguous memory structure, unlike Arrays. LinkedList elements are linked with pointers.

Describe singly-linked lists.

There is a type of linked list called a singly linked list, and this type of list is unidirectional; that is, it can only be traversed from head to tail.

Would it be better to use iteration or recursion?

It can sometimes be more challenging to determine the time complexity of recursive code than iterative code. In comparison to iteration, recursion has a lot of overhead. Due to the fact that all function calls must be stored on a stack, it is typically much slower. There is no such overhead with iteration.

Conclusion

In this blog, we have seen how to find the length of a LinkedList using iterative and Recursive methods.

We hope that this blog has helped you enhance your knowledge about LinkedList and if you would like to learn more about Doubly Linked List, Linked List advantages, limitations, etc. check out our articles on the link.

You can use the Coding Ninjas Studio Guided Path to learn data structures and algorithms, programming languages, etc. Test your coding skills by participating in the Coding Ninjas Studio contests and tests! But if you have just started your learning process and looking for questions asked by tech giants like Amazon, Microsoft, Uber, etc; you must have a look at the problems, interview experiences, and interview bundle for placement preparations.

Nevertheless, you may consider our paid courses to give your career an edge over others!

Do upvote our blogs if you find them helpful and engaging!

Happy Coding!