Length of the Loop in the Linked List

Introduction

The linked list data structure is one of the most important topics in technical interviews. It forms a variety of tricky yet straightforward questions. This article explains one such question in detail.

Finding whether a linked list contains a loop is one of the classic problems of a linked list. A slight variation of this question is to find the length of the loop in the linked list.
 

So, let’s get started!

Problem Statement

Given a singly linked list, we've to find the length of the loop in the linked list if a loop is present. If there is no loop, return 0.

For example, a loop can be found in the linked list below, and its length is 6. 

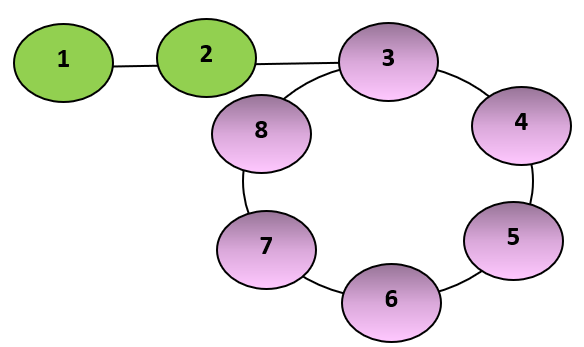
Solution Approach

This solution to this problem can be broken down into two parts to reduce its complexity.

Part-1: Detect if linked list has a loop

Part-2: Finding the length of the loop.

Part-1:

Floyd’s cycle detection algorithm is used to check whether the linked list contains a cycle or not. It uses a two-runner approach to do so. Let’s first understand this algorithm in brief.
 

The fast runner and slow runner approach is an easy way to detect if a linked list has a loop. A fast runner moves two steps at a time, while a slow runner moves one step. If there is a loop, they must collide at some point. This is how Floyd's cycle detection algorithm works.

To learn about this algorithm in detail, we suggest you read this fantastic blog, Floyd’s cycle detection algorithm.

We’ll be using this algorithm to solve the first part of this problem. 

Part-2:

The point at which the fast runner and the slow runner will meet, let's call it the point of collision. In a pointer variable, we'll store the collision point's address. Then, starting from the collision point, increment the counter as we visit each node until we reach the collision point again.

At this time, the counter's value will be equal to the length of the loop in the linked list. Now, simply return the counter value.

Let’s see the implementation of this approach.

Implementation

The implementation of the above approach to find the length of the loop in the linked list is given below:

//Program to find the length of the loop in the linked list

#include<bits/stdc++.h>

using namespace std;



struct Node

{

	int data;

	struct Node* next;

};



// Function to find the length of the loop in the linked list.

int lengthOfLoop(struct Node *n)

{

	int ans =  1;

	struct Node *temp =  n;

	while (temp->next != n)

	{

		ans++;

		temp = temp->next;

	}

	return ans;

}



//Function to detect loop

int isLoopPresent(struct Node *list)

{

	int temp = 0;

	struct Node *S_runner =  list; // slow runner

	    struct Node *F_runner =  list; // fast runner



	while (S_runner !=  NULL && F_runner !=  NULL && F_runner->next !=  NULL)

	{

		S_runner = S_runner->next;

		F_runner = F_runner->next->next;



// Point of collision

		if (S_runner == F_runner)

			return lengthOfLoop(S_runner);

	}



	   // if no loop is present

	return temp;

}



struct Node *newNode(int key)

{

	struct Node *ptr = (struct Node*)malloc(sizeof(struct Node));

	ptr->data = key;

	ptr->next =  NULL;

	return ptr;

}

// Driver Code

int main()

{

	struct Node *head =  newNode(17);

	head->next = newNode(21);

	head->next->next = newNode(33);

	head->next->next->next = newNode(49);

	head->next->next->next->next = newNode(18);

	head->next->next->next->next->next = newNode(57);

	head->next->next->next->next->next->next = newNode(28);



// loop part

	head->next->next->next->next->next->next->next = head->next;



	int length = isLoopPresent(head);

	if (length >  0)

		       cout << "The length of loop in the linked list is: " << length << endl;

	   else

		       cout << "Loop is not present in the linked list" << endl;



	return 0;

}

You can also try this code with Online C++ Compiler

Run Code

Output:

The length of the loop in the linked list is: 6

Now, let’s move towards frequently asked questions on this topic.