Level Order Traversal of a Binary Tree

Introduction

Binary trees are the specialized version of generic tree data structure where every node can have at most only two children named the left child and right child of a binary tree. We can travel trees in many ways, like pre-order traversal and post-order traversal, but we will learn about level order traversal of Binary trees in this blog.

What is Level order traversal?

In level order traversal, we first visit all the nodes of a previous level before moving on to the next level. Level order traversal is also referred to as Breadth-First search because, in level order traversal, we cover the breadth of a tree first. Let’s understand it better with the below image:

Let’s suppose we have the above binary tree with the root node as 1. Then we have to write its level order traversal. To write level order traversal, we have to go level by level. First, write all the nodes present at level 0, then write all nodes present at level 1, and so on ……

Hence the level order traversal of this binary tree will be:

1, 2, 3, 4, 5, 6, 7

Let’s learn how to code for printing a level order traversal of a binary tree.

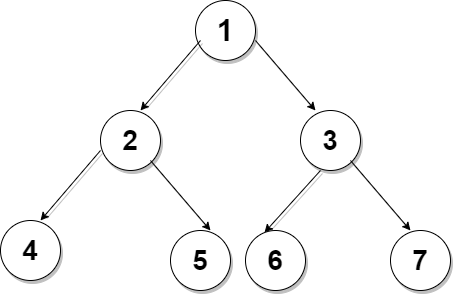
Brute-force Approach

This approach is not the optimized one but in an interview, you are expected to start from a brute-force approach. So before moving on to an optimized approach we should understand this first:

Step 1. Calculate the height of the binary tree, let us denote this by h. The number of different levels in the binary tree will be equal to this height.

Step 2. For every level ‘lvl’ from 1 to h print the nodes present at lvl. For printing the nodes at the current level lvl we make a recursive call starting from the root of the binary tree with lvl as a parameter and recursively call the function on the left and right child respectively by decreasing the lvl parameter each time we move one step in depth and print the nodes when the current level lvl becomes 1.

Since the call to function is made in order of left and right child respectively, the nodes at each level are printed from left to right.

After this step, you will have your correct output.

Below is the implementation of the above approach:

C

#include <stdio.h>
#include <stdlib.h>

// Binary tree structure
struct Node {
    int data;
    struct Node* left;
    struct Node* right;
};

// Function to create a new node
struct Node* newNode(int data) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// Function to print nodes at the current level
void printCurrLevel(struct Node* root, int level) {
    if (root == NULL)
        return;
    if (level == 1)
        printf("%d ", root->data);
    else if (level > 1) {
        printCurrLevel(root->left, level - 1);
        printCurrLevel(root->right, level - 1);
    }
}

// Function to find the height of the tree
int height(struct Node* node) {
    if (node == NULL)
        return 0;
    else {
        int lheight = height(node->left);
        int rheight = height(node->right);
        return (lheight > rheight) ? (lheight + 1) : (rheight + 1);
    }
}

// Function to print level order traversal of the tree
void printLevelOrder(struct Node* root) {
    int h = height(root);
    for (int i = 1; i <= h; i++)
        printCurrLevel(root, i);
}

// Main function
int main() {
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);

    printf("Printing level order traversal\n");
    printLevelOrder(root);

    return 0;
}

You can also try this code with Online C Compiler

Run Code

C++

#include <bits/stdc++.h>
using namespace std;


//Binary tree class
class node {
   public:
      //data members
      int data;
       node * left;
       node* right;
};


/* Function prototypes */
void printCurrLevel(node * root, int level);
int height(node * node);
node * newNode(int data);


/* Function to print level
order traversal a tree*/
void printLevelOrder(node * root) {
   int h = height(root);
   for (int i = 1; i <= h; i++)
      printCurrLevel(root, i);
}


/* Print nodes at a current level */
void printCurrLevel(node * root, int level) {
   if (root == NULL)
      return;
   if (level == 1)
      cout << root -> data << " ";
   else if (level > 1) {
      //call on left child
      printCurrLevel(root -> left, level - 1);
      //call on right child
      printCurrLevel(root -> right, level - 1);
   }
}


//function to get the height of tree
int height(node * node) {
   if (node == NULL)
      return 0;
   else {
      /* compute the height of each subtree */
      int lheight = height(node -> left);
      int rheight = height(node -> right);


      /* use the larger one */
      if (lheight > rheight) {
         return (lheight + 1);
      } else {
         return (rheight + 1);
      }
   }
}


//This function will help in creating a new node
node * newNode(int data) {
   node * Node = new node();
   Node -> data = data;
   Node -> left = NULL;
   Node -> right = NULL;


   return (Node);
}


int main() {
   node * root = newNode(1);
   root -> left = newNode(2);
   root -> right = newNode(3);
   root -> left -> left = newNode(4);
   root -> left -> right = newNode(5);


   cout << "Printing level order traversal";
   printLevelOrder(root);


   return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Java

class Node {
    int data;
    Node left, right;

    Node(int item) {
        data = item;
        left = right = null;
    }
}

class BinaryTree {
    Node root;

    // Function to print level order traversal of tree
    void printLevelOrder() {
        int h = height(root);
        for (int i = 1; i <= h; i++)
            printCurrLevel(root, i);
    }

    // Function to find height of tree
    int height(Node root) {
        if (root == null)
            return 0;
        else {
            int lheight = height(root.left);
            int rheight = height(root.right);
            return (lheight > rheight) ? (lheight + 1) : (rheight + 1);
        }
    }

    // Function to print nodes at a given level
    void printCurrLevel(Node root, int level) {
        if (root == null)
            return;
        if (level == 1)
            System.out.print(root.data + " ");
        else if (level > 1) {
            printCurrLevel(root.left, level - 1);
            printCurrLevel(root.right, level - 1);
        }
    }

    public static void main(String args[]) {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);

        System.out.println("Printing level order traversal");
        tree.printLevelOrder();
    }
}

You can also try this code with Online Java Compiler

Run Code

Python

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

def height(node):
    if node is None:
        return 0
    else:
        lheight = height(node.left)
        rheight = height(node.right)
        return max(lheight, rheight) + 1

def print_curr_level(node, level):
    if node is None:
        return
    if level == 1:
        print(node.data, end=" ")
    elif level > 1:
        print_curr_level(node.left, level - 1)
        print_curr_level(node.right, level - 1)

def print_level_order(root):
    h = height(root)
    for i in range(1, h + 1):
        print_curr_level(root, i)

root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)

print("Printing level order traversal")
print_level_order(root)

You can also try this code with Online Python Compiler

Run Code

Javascript

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

function height(node) {
    if (node === null)
        return 0;
    else {
        let lheight = height(node.left);
        let rheight = height(node.right);
        return Math.max(lheight, rheight) + 1;
    }
}

function printCurrLevel(node, level) {
    if (node === null)
        return;
    if (level === 1)
        process.stdout.write(node.data + " ");
    else if (level > 1) {
        printCurrLevel(node.left, level - 1);
        printCurrLevel(node.right, level - 1);
    }
}

function printLevelOrder(root) {
    let h = height(root);
    for (let i = 1; i <= h; i++)
        printCurrLevel(root, i);
}

let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);

console.log("Printing level order traversal");
printLevelOrder(root);

You can also try this code with Online Javascript Compiler

Run Code

C#

using System;

public class Node {
    public int data;
    public Node left, right;

    public Node(int item) {
        data = item;
        left = right = null;
    }
}

public class BinaryTree {
    public Node root;

    public void printLevelOrder() {
        int h = height(root);
        for (int i = 1; i <= h; i++)
            printCurrLevel(root, i);
    }

    int height(Node node) {
        if (node == null)
            return 0;
        else {
            int lheight = height(node.left);
            int rheight = height(node.right);
            return (lheight > rheight) ? (lheight + 1) : (rheight + 1);
        }
    }

    void printCurrLevel(Node root, int level) {
        if (root == null)
            return;
        if (level == 1)
            Console.Write(root.data + " ");
        else if (level > 1) {
            printCurrLevel(root.left, level - 1);
            printCurrLevel(root.right, level - 1);
        }
    }

    public static void Main(string[] args) {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);

        Console.WriteLine("Printing level order traversal");
        tree.printLevelOrder();
    }
}

Output:

Printing level order traversal
1 2 3 4 5

Complexity Analysis

Time Complexity

The time complexity is O(N^2) where N refers to the number of nodes in a binary tree. Suppose you got a skewed tree as input then the complexity of printLevelOrder will be O(N)+O(N-1)+....... Which will lead to O(N^2).

Space Complexity

The Space Complexity is O(N) where N refers to the number of nodes in a binary tree. As we are using recursion here, we will be using O(N) space for the call stack.

Level Order Traversal Using Queue

This is the optimized approach for the level order traversal of a binary tree.

Here we will make use of a queue data structure i.e First In First Out. We first push a node and then its left and right child into the queue in this approach.

Let’s discuss this approach in steps but before that promise me that you will try to code it on your own after going through these steps. Okay, so let’s see the steps:-

Step 1. Take an empty queue and push the root node into the queue.

Step 2. While the queue is non-empty perform the following steps:

Pop the front element from the queue and print it.
Push the left child and right child of the popped node if they exist in the queue.

On the termination of this while loop, you will have the level order traversal as your output.

As promised, have you tried coding it?

Below is the Implementation of the above approach:

C

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int data;
    struct Node* left, * right;
};

struct Node* newNode(int data) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->data = data;
    node->left = node->right = NULL;
    return node;
}

void printLevelOrder(struct Node* root) {
    if (root == NULL)
        return;
    struct Node* queue[1000];
    int front = 0, rear = 0;
    queue[rear++] = root;
    while (front < rear) {
        struct Node* temp = queue[front++];
        printf("%d ", temp->data);
        if (temp->left != NULL)
            queue[rear++] = temp->left;
        if (temp->right != NULL)
            queue[rear++] = temp->right;
    }
}

int main() {
    struct Node* root = newNode(11);
    root->left = newNode(12);
    root->right = newNode(13);
    root->left->left = newNode(14);
    root->left->right = newNode(15);

    printf("Printing the level order traversal\n");
    printLevelOrder(root);

    return 0;
}

You can also try this code with Online C Compiler

Run Code

C++

#include <iostream>
#include <queue>
using namespace std;

class Node {
public:
    int data;
    Node* left, * right;

    Node(int item) {
        data = item;
        left = right = NULL;
    }
};

class BinaryTree {
public:
    Node* root;

    void printLevelOrder() {
        if (root == NULL)
            return;
        queue<Node*> q;
        q.push(root);
        while (!q.empty()) {
            Node* temp = q.front();
            q.pop();
            cout << temp->data << " ";
            if (temp->left != NULL)
                q.push(temp->left);
            if (temp->right != NULL)
                q.push(temp->right);
        }
    }
};

int main() {
    BinaryTree tree_level;
    tree_level.root = new Node(11);
    tree_level.root->left = new Node(12);
    tree_level.root->right = new Node(13);
    tree_level.root->left->left = new Node(14);
    tree_level.root->left->right = new Node(15);

    cout << "Printing the level order traversal\n";
    tree_level.printLevelOrder();

    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Java

import java.util.Queue;
import java.util.LinkedList;

 
/* Class to represent Tree node */
class Node {
    //data members
    int data;
    Node left, right;

 
    public Node(int item) {
        data = item;
        left = null;
        right = null;
    }
}

 
class BinaryTree {
    Node root;

 
    //printing the node in level order
    void printLevelOrder() {
        Queue < Node > queue = new LinkedList < Node > ();
        queue.add(root);
        while (!queue.isEmpty()) {

 
            //poll will remove the current head
            Node front = queue.poll();
            System.out.print(front.data + " ");

 
            /*This will be adding the left child into the queue */
            if (front.left != null) {
                queue.add(front.left);
            }

 
            /*This will adding the right child in the queue */
            if (front.right != null) {
                queue.add(front.right);
            }
        }
    }

 
    public static void main(String args[]) {
        /* creating a binary tree and entering
         the nodes */
        BinaryTree tree_level = new BinaryTree();
        tree_level.root = new Node(11);
        tree_level.root.left = new Node(12);
        tree_level.root.right = new Node(13);
        tree_level.root.left.left = new Node(14);
        tree_level.root.left.right = new Node(15);

 
        System.out.println("Printing the level order traversal ");
        tree_level.printLevelOrder();
    }
}

You can also try this code with Online Java Compiler

Run Code

Python

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

def printLevelOrder(root):
    if root is None:
        return
    queue = []
    queue.append(root)
    while len(queue) > 0:
        temp = queue.pop(0)
        print(temp.data, end=" ")
        if temp.left is not None:
            queue.append(temp.left)
        if temp.right is not None:
            queue.append(temp.right)

root = Node(11)
root.left = Node(12)
root.right = Node(13)
root.left.left = Node(14)
root.left.right = Node(15)

print("Printing the level order traversal")
printLevelOrder(root)

You can also try this code with Online Python Compiler

Run Code

Javascript

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

function printLevelOrder(root) {
    if (root === null)
        return;
    const queue = [];
    queue.push(root);
    while (queue.length > 0) {
        let temp = queue.shift();
        process.stdout.write(temp.data + " ");
        if (temp.left !== null)
            queue.push(temp.left);
        if (temp.right !== null)
            queue.push(temp.right);
    }
}

let root = new Node(11);
root.left = new Node(12);
root.right = new Node(13);
root.left.left = new Node(14);
root.left.right = new Node(15);

console.log("Printing the level order traversal");
printLevelOrder(root);

You can also try this code with Online Javascript Compiler

Run Code

C#

using System;
using System.Collections.Generic;

public class Node {
    public int data;
    public Node left, right;

    public Node(int item) {
        data = item;
        left = right = null;
    }
}

public class BinaryTree {
    public Node root;

    public void printLevelOrder() {
        if (root == null)
            return;
        Queue<Node> queue = new Queue<Node>();
        queue.Enqueue(root);
        while (queue.Count > 0) {
            Node temp = queue.Dequeue();
            Console.Write(temp.data + " ");
            if (temp.left != null)
                queue.Enqueue(temp.left);
            if (temp.right != null)
                queue.Enqueue(temp.right);
        }
    }
}

class Program {
    public static void Main(string[] args) {
        BinaryTree tree_level = new BinaryTree();
        tree_level.root = new Node(11);
        tree_level.root.left = new Node(12);
        tree_level.root.right = new Node(13);
        tree_level.root.left.left = new Node(14);
        tree_level.root.left.right = new Node(15);

        Console.WriteLine("Printing the level order traversal");
        tree_level.printLevelOrder();
    }
}

Output:

Printing the level order traversal
11 12 13 14 15

Complexity Analysis

Time Complexity

Time complexity will be O(N), where N is the number of nodes in a binary tree. Since we are visiting each node of the binary tree and putting each node in the queue, the time complexity will be linear.

Space Complexity

The space complexity of this approach will be O(N) where N is the number of nodes in a binary tree.

We are using a queue to store each one of the binary trees.

Frequently Asked Questions

Is level order traversal same as inorder traversal?

No, level order traversal and inorder traversal are different. Level order traversal traverses the tree level by level, starting from the root, while inorder traversal visits nodes in non-decreasing order recursively, typically used for binary search trees.

What is the other name of Level order traversal?

Level order traversal is also known as Breadth-first search as we cover the breadth of the tree first rather than height.

Can I achieve the level order of traversal of a tree without using a queue?

Yes, you can as we have discussed in method 1 of this blog. But this will cost you more in terms of time complexity as without a queue your time complexity will be O(N^2).

What is the benefit of using Level order traversal?

Level order traversal or Breadth-first search helps you in finding the shortest distance between two nodes.

Can I use stack instead of the queue to get the level order traversal of a binary tree?

No! You have to use queue only because we want to get nodes we have entered first as the first output and it can only be achieved using the First In First Out property of the queue data structure.

Conclusion

In this blog, we have discussed all the two approaches for the level order traversal of a binary tree. But remember, the approach discussed using a queue is the most optimized one, and you are expected to come up with this approach in your interviews. One more thing to remember here is that level order traversal is also referred to as Breadth-first search.

Recommended Reading: