Introduction
Lexicographic order is the generic order in which alphabets and symbols are sequenced. Starting from A to Z, Z is the largest alphabet, while A is the smallest. Considering we have a string ‘str’ and a positive integer ‘k’, our task will be to find the lexicographically largest string possible in str using k swaps at the same parity indices. At the same parity, indices signify that the elements to be swapped must be at the even or odd indices.
Let us now have a look at some examples for better understanding:
Sample Examples
First, the trick is to assess all the elements at odd and even indices, respectively, decide which ones are the largest lexicographically, and then plan swaps accordingly.
Example 1:
Input:
str=hello, k=2
Output:
olleh
Considering 1-indexing,
Largest to smallest elements at odd indices: o, l, h
Largest to smallest elements at even indices: l, e
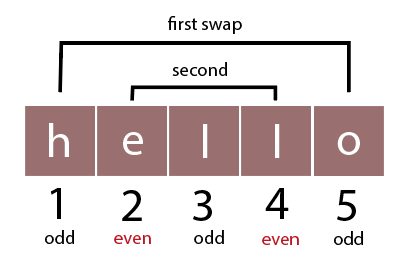
In the first swap, we will interchange ‘e’, and ‘l’ at even indices, and the string will become ‘hlleo’.
In the second swap, we will interchange ‘o’ and ‘h’ at odd indices. The string will now be ‘olleh’
Example 2:
Input:
kszix, k=2
Output:
zsxik
Largest to smallest elements at odd indices: z, x, k
Largest to smallest elements at even indices: s, i
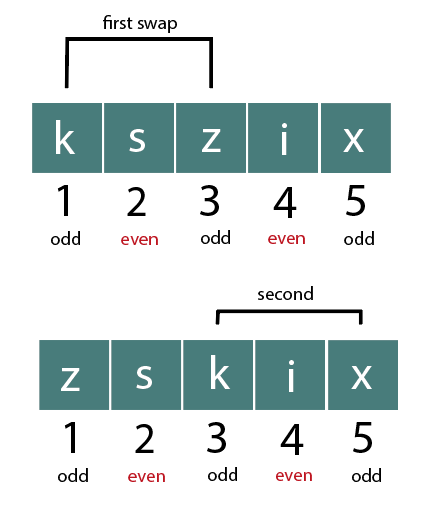
In the first swap, we will interchange ‘k’, and ‘z’ at odd indices, and the string will become ‘zskix’.
In the second swap, we will interchange ‘k’ and ‘x’ at even indices. The string will now be ‘zsxik’
(Also see Data Structures)
Brute force approach
The most straightforward approach is to make the leftmost elements the maximum possible. The largest element on odd indices can first be brought to index 1 first. The largest element on even indices can be brought to index 2. The second largest element on odd indices can be brought to index 3 and so on. Then, we will repeat the procedure K times.
Implementation in C++
#include<bits/stdc++.h>
using namespace std;
void findMax(string s , int k)
{
int n = s.length();
int count = 0;
int max, index = 0;
for (int i = 0; i < n; i++)
{
max = s[i];
for (int j = i + 2; j < n; j += 2)
{
if (s[j] > max)
{
index = j;
max = s[j];
}
}
if (index != 0)
{
swap(s[i], s[index]);
index = 0;
count++;
}
if (count == k)
break;
}
cout << s << endl;
}
int main()
{
string s = "salty";
int k = 2;
findMax(s, k);
}
Output
ytlasImplementation in Java
import java.util.*;
public class Main {
static String swap(String str, int i, int j)
{
StringBuilder sb = new StringBuilder(str);
sb.setCharAt(i, str.charAt(j));
sb.setCharAt(j, str.charAt(i));
return sb.toString();
}
public static void findMax(String s , int k)
{
int n = s.length();
int count = 0;
int max, index = 0;
for (int i = 0; i < n; i++)
{
max = s.charAt(i);
for (int j = i + 2; j < n; j += 2)
{
if (s.charAt(j) > max)
{
index = j;
max = s.charAt(j);
}
}
if (index != 0)
{
s=swap(s,i, index);
index = 0;
count++;
}
if (count == k)
break;
}
System.out.println(s);
}
public static void main(String args[]) {
String s = "salty";
int k = 2;
findMax(s, k);
}
}Output
ytlasImplementation in Python
def swap(str,i,j):
str=list(str)
temp1=str[i]
str[i]=str[j]
str[j]=temp1
string1=""
return string1.join(str)
def findMax(s , k):
n = len(s)
count = 0
maxi=0
index = 0
for i in range(0,n):
maxi = s[i]
j=i+2
while(j<n):
if (s[j] > maxi):
index = j
maxi = s[j]
j+=2
if (index != 0):
s=swap(s,i, index)
index = 0
count+=1
if (count == k):
break
print(s)
s = "salty";
k = 2;
findMax(s, k);Output
YtlasComplexity Analysis
Time Complexity: O(N^2)
Since the brute force approach uses nested for loops to compare elements at the same parity indices, the time complexity of such an approach will be O(N^2).
Note that lexicographically largest string problems are all different and have different conditions, such as having a limited number of swaps, only allowing some particular swaps(in this case only even or only odd indices), etc. However, the basic approach toward such problems will remain the same. We could use techniques like bubble sort for lesser constraints and simpler problems, just swapping according to the condition for the brute force, or using priority queues for the least time complexity.
Space complexity: O(1)
The space complexity will be O(1) as we are not using any extra space and have just used variables for maintaining the answer.




