Data Pre-Processing
i. Boston data frame shape
print("Shape: ",boston.shape) #examining the number of rows and columns in the data

You can also try this code with Online Python Compiler
Output
Shape : (506, 14)
ii. Checking null values
It's a good idea to check the data after it's been loaded to see any missing values. isnull() function is used to count the number of missing values for each characteristic.
# checking if there is any null value
boston.isnull().values.any()

You can also try this code with Online Python Compiler
However, as shown below, there are no missing values in this dataset.
Output
False
iii. Print Statistical Description
boston.describe()

You can also try this code with Online Python Compiler
Output

Exploratory Data Analysis & Visualization
Exploratory Data Analysis is a critical phase in the model training process. We'll utilize visualizations in this part to better comprehend the relationship between the target variable and other characteristics.
Let's start with a visualization of the target variable Price’s distribution. We will use the distplot() function from the seaborn library.
# fix the figure size
sns.set(rc={'figure.figsize':(12,9)})
# Create a histogram that depicts the target values' distribution.
sns.distplot(boston['Price'], bins=30)
plt.show()

You can also try this code with Online Python Compiler
Output

We can see that Price values are normally distributed with few outliers.
After that, we create a correlation matrix to determine the linear relationships between the variables. We can use the corr() function from the pandas data frame library to generate the correlation matrix. The correlation matrix will be shown using the heatmap() function from the seaborn library.
# for all columns, compute the pairwise correlation
correlationMatrix = boston.corr().round(2)
# To plot the correlation matrix, we use the heatmap function from seaborn.
# annot = True (for printing the values inside the square)
sns.heatmap(data=correlationMatrix, annot=True)

You can also try this code with Online Python Compiler
Output

The correlation coefficient might be anything between -1 and 1. If the value is near 1, it suggests that the two variables have a high positive association. The variables have a high negative association when it is close to -1.
Remarks
-
We choose features that have a high correlation with our target variable, Price, to fit a linear regression model. The correlation matrix shows that RM has a high positive correlation (0.7) with Price, whereas LSTAT has a strong negative correlation with Price (-0.74).
-
Checking for multi-co-linearity is a crucial consideration when choosing features for a linear regression model. The features RAD and TAX have a 0.91 correlation. These feature pairs have a high degree of correlation. When training the model, we should not use both of these features together. The same may be said for the features DIS and AGE, which exhibit a -0.75 correlation.
We will use RM and LSTAT as our features based on the preceding observations. Let's look at how these characteristics change with Price using a scatter plot.
plt.figure(figsize=(20, 5))
features = ['LSTAT', 'RM']
target = boston['Price']
for j, column in enumerate(features):
plt.subplot(1, len(features) , j+1)
x = boston[column]
y = target
plt.scatter(x, y, marker='o')
plt.title(column)
plt.xlabel(column)
plt.ylabel('Price')

You can also try this code with Online Python Compiler
Output
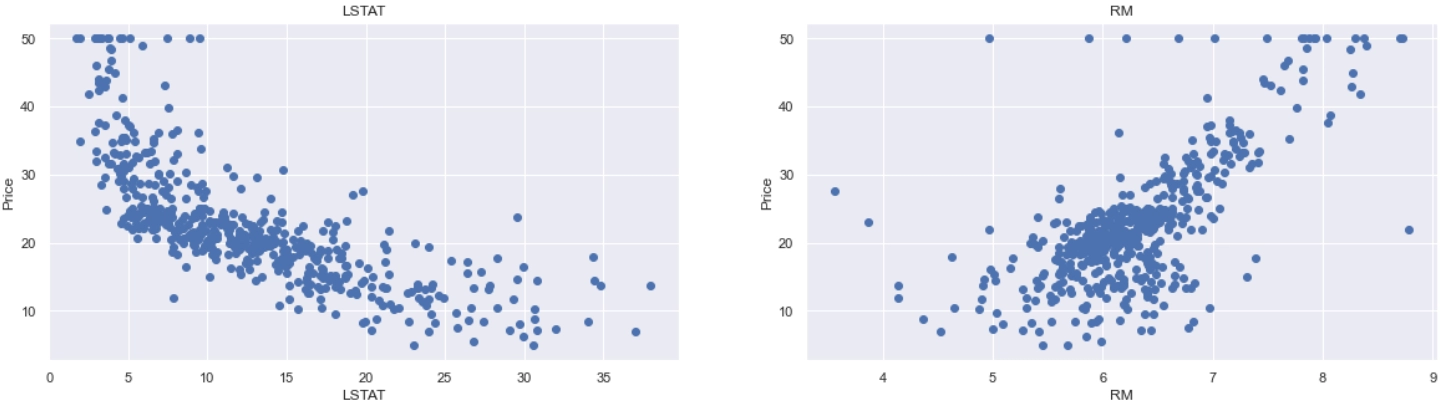
Remarks
-
The price increases linearly with the value of the RM. There aren't many outliers, and the data appears to be limited to 50.
-
With a rise in LSTAT, prices tend to fall. However, it doesn't appear to be following a straight line.
Getting the data ready to train the model
Using the NumPy library's np.c_() function, we concatenate the LSTAT and RM columns.
X = pd.DataFrame(np.c_[boston['LSTAT'], boston['RM']], columns = ['LSTAT','RM'])
Y = boston['Price']

You can also try this code with Online Python Compiler
Modeling and Prediction
Splitting the data into training and testing sets
The data is then divided into training and testing sets. We use 80% of the samples to train the model and 20% to evaluate it. This is done to assess the model's performance with data that hasn't been seen before. To separate the data, we utilize the scikit-learn library's train_test_split() function. Finally, we printed the sizes of our training and test sets to ensure that the splitting went smoothly.
from sklearn.model_selection import train_test_split
# splits the training and test data set in 80% : 20%
# to ensure consistency assign any value to random_state
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state=5)
print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)

You can also try this code with Online Python Compiler
Output
(404, 2)
(102, 2)
(404,)
(102,)
Training and testing the model
We use scikit-learn's LinearRegression() to train our model on both the training and test sets.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
regressor = LinearRegression()
regressor.fit(X_train, Y_train)

You can also try this code with Online Python Compiler
Model Evaluation
Model Evaluation calculates generalized accuracy for data that hasn't been seen before. It also determines whether or not our model is overfitting. Overfitted models perform well on test datasets but do not predict well on real-world datasets. Therefore, if there is no significant difference in the accuracy of the train and test sets, we can say that our model is ready for deployment.
The Root Mean Square Error (RMSE) and R2-score will be used to assess our model.
# model evaluation for the training set
predicted_y_train = regressor.predict(X_train)
rmse = (np.sqrt(mean_squared_error(Y_train, predicted_y_train)))
r2 = r2_score(Y_train, predicted_y_train)
print("The model's training set performance :-")
print('RMSE is : {}'.format(rmse))
print('R2 score is : {}'.format(r2))
print("--------------------------------------")
# model evaluation for Test set
predicted_y_test = regressor.predict(X_test)
# root mean square error of the model
rmse = (np.sqrt(mean_squared_error(Y_test, predicted_y_test)))
# r-squared score of the model
r2 = r2_score(Y_test, predicted_y_test)
print("The model's testing set performance")
print('RMSE is : {}'.format(rmse))
print('R2 score is : {}'.format(r2))
print("--------------------------------------")

You can also try this code with Online Python Compiler
Output
The model's training set performance :-
RMSE is : 5.6371293350711955
R2 score is : 0.6300745149331701
--------------------------------------
The model's testing set performance
RMSE is: 5.137400784702911
R2 score is: 0.6628996975186952
--------------------------------------
As there isn’t much difference between the R2 score of the Training and Test set. The R2 score is close to 1. Therefore we can conclude that the model isn’t overfitted
Check out this problem - First Missing Positive
Frequently Asked Questions
What is Linear Regression?
Linear Regression is used to predict the value of a variable based on another variable.
What are dependent and independent variables in Linear Regression?
The variable which is used to predict another variable is called the independent variable whereas the variable that is being predicted is called the dependent variable.
What is Overfitting?
Overfitting occurs when a model fits exactly against its training data. These are suboptimal in nature when dealing with unseen data. Linear Models rarely overfit.
Conclusion
Cheers if you reached here!! In this blog, we used linear regression to predict prices on the Boston Housing Dataset.
Recommended Readings:
Check out some of the amazing Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Basics of C, etc. along with some Contests and Interview Experiences only on Coding Ninjas Studio.
Yet learning never stops, and there is a lot more to learn. Happy Learning!!
Cheers;)










