Rehashing in Data Structure

Introduction

HashMap is a popular Data structure for storing key-value pairs that can be used to solve a variety of problems. Both search() and insert() operations on HashMap have a constant O(1) time complexity. One of the most frequently asked questions on HashMap is about rehashing. To understand rehashing in Data Structure, we must first understand the load factor and why it is used.

Briefly, the load factor measures how full the hash table is allowed to get before its capacity is automatically increased. It is very important as it is used to measure the performance of our hashmap.

Before coming to rehashing and in-depth analysis of load factor, let’s brush up on our concepts on the basic hashing principle used by HashMap.

(Recommended, Try Implementation of Hashmap)

Also Read About - hash function in data structure

What is Rehashing?

Rehashing is the process of recalculating the hashcode of previously-stored entries (Key-Value pairs) in order to shift them to a larger size hashmap when the threshold is reached/crossed,

When the number of elements in a hash map reaches the maximum threshold value, it is rehashed.

According to the Java specification, the good load factor value is 75, while HashMap's default beginning capacity is 16. When the number of elements hits or exceeds 0.75 times the capacity, the complexity rises. To combat this, the array's size is doubled, and all the values are hashed again and saved in the new double-sized array. This is done in order to simplify things and keep the focus on the important things and keep the load factor low.

So, when the number of items reaches 12, rehashing begins. (as 12 = 0.75 * 16).

After Rehashing items can fall into same bucket or different bucket into new array.

But what is the need for rehashing?

Why Rehashing in Data Structure?

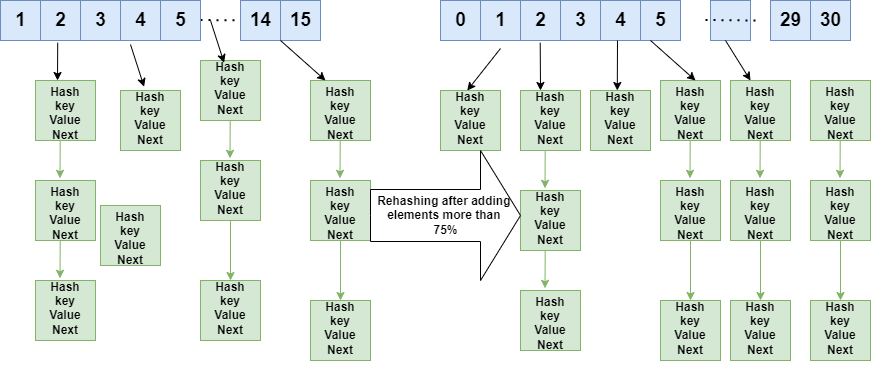
The reason for rehashing is that anytime a new key-value pair is placed into the map, the load factor rises, and as a result, the complexity rises as well. And as the complexity of our HashMap grows, it will no longer have a constant O(1) time complexity. As a result, rehashing is used to disperse the items across the hashmap, lowering both the load factor and the complexity, resulting in search() and insert() having a constant time complexity of O(1). One should note that the existing objects may fall into the same or a different category after rehashing.

(Also see, Space Complexity)

Now that we know what rehashing is and why it is important, it is equally important to know how rehashing is done.

How Rehashing is done?

Rehashing can be done in the following way:

Check the load factor after adding a new entry to the map.
Rehash if it is more than the pre-defined value (or the default value of 0.75 if none is specified).
Make a new bucket array that is double the size of the previous one for Rehash.
Then go through each element in the old bucket array, calling insert() on each to add it to the new larger bucket array.

Try some Practise Problems

What is Load Factor?

Load factor is a measure that helps to decide when to increase the HashTable or HashMap capacity to maintain the operations(search and insert) complexity of O(1). The default value of the load factor is 0.75, i.e. 75% of the HashMap size.

Load factor can be decided using the formula as follows:

The initial capacity of the HashMap * Load factor of the HashMap

Let's understand Load Factor with the help of an example.

For example if the initial capacity of Hashtable is 20 and the load factor of hastable is 0.75(default value), then according to the formula 20*0.75 = 15.

It means the 15th key-value pair of the hashtable will keep its size as 20. Now when we insert the 16th key-value pair into the hashtable, it will increases its size from 20 to 20*2 = 40 buckets.

Load Factor and Complexity

The time it takes to complete the first step is determined by the key, 'K', and the hash function.

If the key is a string like "abcd," let's say our hash function depends on the length of the string. For example, it could be adding the ASCII values of all characters and taking the modulo of that by 100.

However, for very large values of 'N', the number of entries in the map, and the length of the keys is virtually small compared to ‘N’. Hence hash computation can be assumed to run in constant time, i.e., O(1).

The second step consists of traversing the list of K-V pairs that exist at that index. The worst-case scenario is that all ‘N’ entries are at the same index. As a result, the time complexity would be O(N). However, enough study has been done to ensure that hash functions are evenly distributed. As a result, this nearly never happens.

So, on average, if there are ‘N’ entries and ‘B’ is the array size, each index will have N/B entries. This N/B figure is known as the load factor, and it represents the load on our map.

This load factor should be kept low such that the number of entries in each index is reduced and the complexity remains relatively constant, i.e., O(1).

Rehashing Steps in Data Structure

The rehashing process contain the following steps:

First of all check the load factor of the insertion of each new element to the HashMap.
If the load factor is greater than its default value i.e. 0.75, then implement rehashing technique.
Create a new array of the size double than the size of the previous array.
Iterate over the previous array elements and on each element make a call to the insert() method. The insert() method inserts all the elements in the newly created array(larger in size).

Implementation of Rehashing in Java

import java.util.ArrayList;  
class Map<k, v>   
{  
	class Node<k, v>   
	{  
		k key;  
		v value;  
		Node<k, v> next;  

		public Node(k key, v value)  
		{  
			this.key = key;  
			this.value = value;  
			next = null;  
		}  
	}  
	ArrayList<Node<k, v> > List;  

	int size;  
	int num_Buckets;  
	final double Default_LF = 0.75;  
	public Map()  
	{  
  
		num_Buckets = 5;  
		List = new ArrayList<>(num_Buckets);  
		for (int i = 0; i < num_Buckets; i++)   
		{  

			List.add(null);  
		}  
 
		System.out.println("Map is created..");  
		System.out.println("Total number of pairs in the Map: " + size);  
		System.out.println("Size of HashMap: " + num_Buckets);  
		System.out.println("Default Load Factor is : " + Default_LF + "\n");  
	}  
	private int getBucketInd(k key)  
	{  
		int hashCode = key.hashCode();  
		return (hashCode % num_Buckets);  
	}  
	public void insert(k key, v value)  
	{  
 
		int bucketInd = getBucketInd(key);  
		Node<k, v> head = List.get(bucketInd);  
	 
		while (head != null)   
		{  
 
			if (head.key.equals(key))   
			{  
				head.value = value;  
				return;  
			}  
			head = head.next;  
		}  
		Node<k, v> newElement = new Node<k, v>(key, value);  
	
		head = List.get(bucketInd);  
 
		newElement.next = head;  
		List.set(bucketInd, newElement);  
		System.out.println("Pair(" + key + ", " + value + ") inserted successfully.\n");  

		size++;  
 
		double lf = (1.0 * size) / num_Buckets;  
		System.out.println("Current Load factor is: " + lf);  
		if (lf > Default_LF)   
		{  
			System.out.println(lf + " is greater than " + Default_LF);  
			System.out.println("As lf is greater than default lf, Rehashing is done\n");  
			rehashing();  
			System.out.println("New Size of Map: " + num_Buckets + "\n");  
		}  
		System.out.println("Number of pairs in the Map: " + size);  
		System.out.println("Size of the Map: " + num_Buckets + "\n");  
	}  
 
	private void rehashing()  
	{  
		System.out.println("Rehashing is Started...");  
 
		ArrayList<Node<k, v> > temp = List;  
		List = new ArrayList<Node<k, v> >(2 * num_Buckets);  
		for (int j = 0; j < 2 * num_Buckets; j++)   
		{  

			List.add(null);  
		}  
		size = 0;  
		num_Buckets = num_Buckets * 2;  
		for (int j = 0; j < temp.size(); j++)   
		{  

			Node<k, v> head = temp.get(j);  
			while (head != null)   
			{  
				k key = head.key;  
				v val = head.value;  
				insert(key, val);  
				head = head.next;  
			}  
		}  
		System.out.println("After Rehashing...\n");  
	}  
	public void print()  
	{  
		ArrayList<Node<k, v> > temp = List;  
		System.out.println("Current HashMap: ");  
		for (int j = 0; j < temp.size(); j++)   
		{  
			Node<k, v> head = temp.get(j);  
			while (head != null)   
			{  
				System.out.println("key = " + head.key + ", value = " + head.value);  
				head = head.next;  
			}  
		}  
		System.out.println();  
	}  
}  
// Main class  
public class Example  
{  
	public static void main(String args[])  
	{  

		Map<Integer, String> mp = new Map<Integer, String>();  
		// insert() method to add the elements and printMap() to print that element.
		mp.insert(1, "Practice");  
		mp.print();  
		mp.insert(2, "At");  
		mp.print();  
		mp.insert(3, "Coding");  
		mp.print();  
		mp.insert(4, "Ninjas");  
		mp.print();  
		mp.insert(5, "Platform");  
		mp.print();  
		mp.insert(6, "For");  
		mp.print();  
		mp.insert(7, "Excellence");  
		mp.print();  
 
	}  
}

Output

Map is created..
Total number of pairs in the Map: 0
Size of HashMap: 5
Default Load Factor is : 0.75
Pair(1, Practice) inserted successfully.
Current Load factor is: 0.2
Number of pairs in the Map: 1
Size of the Map: 5
Current HashMap:
key = 1, value = Practice
Pair(2, At) inserted successfully.
Current Load factor is: 0.4Number of pairs in the Map: 2
Size of the Map: 5
Current HashMap:
key = 1, value = Practicekey = 2, value = At
Pair(3, Coding) inserted successfully.
Current Load factor is: 0.6
Number of pairs in the Map: 3Size of the Map: 5
Current HashMap: key = 1, value = Practice
key = 2, value = At
key = 3, value = Coding
Pair(4, Ninjas) inserted successfully.
Current Load factor is: 0.8
0.8 is greater than 0.75
As lf is greater than default lf, Rehashing is done
Rehashing is Started...
Pair(1, Practice) inserted successfully.
Current Load factor is: 0.1
Number of pairs in the Map: 1
Size of the Map: 10
Pair(2, At) inserted successfully.
Current Load factor is: 0.2Number of pairs in the Map: 2
Size of the Map: 10
Pair(3, Coding) inserted successfully.
Current Load factor is: 0.3
Number of pairs in the Map: 3
Size of the Map: 10
Pair(4, Ninjas) inserted successfully.
Current Load factor is: 0.4
Number of pairs in the Map: 4
Size of the Map: 10
After Rehashing...
New Size of Map: 10
Number of pairs in the Map: 4Size of the Map: 10
Current HashMap:
key = 1, value = Practicekey = 2, value = At
key = 3, value = Coding
key = 4, value = Ninjas
Pair(5, Platform) inserted successfully.
Current Load factor is: 0.5
Number of pairs in the Map: 5
Size of the Map: 10
Current HashMap:key = 1, value = Practicekey = 2, value = Atkey = 3, value = Coding
key = 4, value = Ninjas
key = 5, value = Platform
Pair(6, For) inserted successfully.
Current Load factor is: 0.6
Number of pairs in the Map: 6
Size of the Map: 10
Current HashMap:
key = 1, value = Practice
key = 2, value = At
key = 3, value = Codingkey = 4, value = Ninjas
key = 5, value = Platform
key = 6, value = ForPair(7, Excellence) inserted successfully.
Current Load factor is: 0.7Number of pairs in the Map: 7
Size of the Map: 10
Current HashMap: key = 1, value = Practice
key = 2, value = At
key = 3, value = Codingkey = 4, value = Ninjas
key = 5, value = Platform
key = 6, value = For
key = 7, value = Excellence

Implementation of Rehashing in Python

class Map:
class Node:
 def __init__(self,key,value):
  self.key=key
  self.value=value
  self.next=None
List=list()

size=0
num_Buckets=0
Default_lf = 0.75
def __init__(self):
 Map.num_Buckets = 5
 Map.List = [None]*Map.num_Buckets
 print("HashMap created....")
 print("Total number of pairs in the Map: " + str(Map.size))
 print("Size of HashMap is: " + str(Map.num_Buckets))
 print("Default Load Factor is : " + str(Map.Default_lf) + "\n")
def getIndex(self,key):

 hashCode = hash(key)
 
 return (hashCode % Map.num_Buckets)
def insert(self,key,value):
 
 bucketIndex = self.getIndex(key)
 
 head = Map.List[bucketIndex]
 
 while (head != None):
  
  if (head.key==key):
   head.value = value
   return
  head = head.next
 
 newElement = Map.Node(key, value)
 
 head = Map.List[bucketIndex]
 
 newElement.next = head
 Map.List[bucketIndex]= newElement
 print("Pair(\" {} \", \" {} \") is inserted successfully....".format(key,value))
 
 Map.size+=1
 
 lf = (1* Map.size) / Map.num_Buckets
 print("Current Load factor = " + str(lf))
 
 if (lf > Map.Default_lf):
  print(str(lf) + " is greater than " + str(Map.Default_lf))
  print("Rehashing will be done...")
  
  self.rehashing()
  print("New Size of HashMap is: " + str(Map.num_Buckets))
 print("Total Number of pairs in the Map: " + str(Map.size))
 print("Size of Map: " + str(Map.num_Buckets))
def rehashing(self):
 print("\nRehashing is Started.....\n")
 
 temp = Map.List
 
 List =(2 * Map.num_Buckets)
 for j in range(2 * Map.num_Buckets):
  Map.List.append(None)
 Map.size = 0
 Map.num_Buckets *= 2
 for j in range(len(temp)):
  head = temp[j]
  while (head != None):
   key = head.key
   val = head.value
   self.insert(key, val)
   head = head.next
 print("\nRehashing is Ended...")
def printMap(self):
 temp = Map.List
 print("Current HashMap: ")
 for j in range(len(temp)):
  head = temp[j]
  while (head != None):
   print("key = \" {} \", val = {}" .format(head.key,head.value))
   head = head.next
 print()

if __name__ == '__main__':

hp = Map()

hp.insert(1, "Practice")
hp.printMap()
hp.insert(2, "At")
hp.printMap()
hp.insert(3, "Coding")
hp.printMap()
hp.insert(4, "Ninjas")
hp.printMap()
hp.insert(5, "Platform")
hp.printMap()

hp.insert(6, "For")
hp.printMap()

hp.insert(7, "Excellence")
hp.printMap()

Output

HashMap created....
Total number of pairs in the Map: 0
Size of HashMap is: 5
Default Load Factor is : 0.75
Pair(" 1 ", " Practice ") is inserted successfully....
Current Load factor = 0.2
Total Number of pairs in the Map: 1
Size of Map: 5
Current HashMap: 
key = " 1 ", val = Practice
Pair(" 2 ", " At ") is inserted successfully....
Current Load factor = 0.4
Total Number of pairs in the Map: 2
Size of Map: 5
Current HashMap: 
key = " 1 ", val = Practice
key = " 2 ", val = At
Pair(" 3 ", " Coding ") is inserted successfully....
Current Load factor = 0.6
Total Number of pairs in the Map: 3
Size of Map: 5
Current HashMap: 
key = " 1 ", val = Practice
key = " 2 ", val = At
key = " 3 ", val = Coding
Pair(" 4 ", " Ninjas ") is inserted successfully....
Current Load factor = 0.8
0.8 is greater than 0.75
Rehashing will be done...
Rehashing is Started.....

Rehashing is Ended...
New Size of HashMap is: 10
Total Number of pairs in the Map: 0
Size of Map: 10
Current HashMap: 
key = " 1 ", val = Practice
key = " 2 ", val = At
key = " 3 ", val = Coding
key = " 4 ", val = Ninjas
Pair(" 5 ", " Platform ") is inserted successfully....
Current Load factor = 0.1
Total Number of pairs in the Map: 1
Size of Map: 10
Current HashMap: 
key = " 1 ", val = Practice
key = " 2 ", val = At
key = " 3 ", val = Coding
key = " 4 ", val = Ninjas
key = " 5 ", val = Platform
Pair(" 6 ", " For ") is inserted successfully....
Current Load factor = 0.2
Total Number of pairs in the Map: 2
Size of Map: 10
Current HashMap: 
key = " 1 ", val = Practice
key = " 2 ", val = At
key = " 3 ", val = Coding
key = " 4 ", val = Ninjas
key = " 5 ", val = Platform
key = " 6 ", val = For
Pair(" 7 ", " Excellence ") is inserted successfully....
Current Load factor = 0.3
Total Number of pairs in the Map: 3
Size of Map: 10
Current HashMap: 
key = " 1 ", val = Practice
key = " 2 ", val = At
key = " 3 ", val = Coding
key = " 4 ", val = Ninjas
key = " 5 ", val = Platform
key = " 6 ", val = For
key = " 7 ", val = Excellence

Applications of Rehashing

Applications of Rehashing are as follows:

Password Verification
Data Structures
File System
Compilers
Message Digest

Must Recommended Topic, Hash Function in Data Structure.

Frequently Asked Questions

Why is Rehashing done?

Rehashing is done to maintain the constant insertion and extraction time complexity in a hashmap, because whenever pairs are inserted into the hashmap the Load Factor(lf) increases, which means the time complexity also increases.

What is rehashing in data structure with example?

Rehashing is a process through which the size of the HashTable, and Array is expanded dynamically to prevent the collisions and improve the performance also. We can say that rehashing is reverse process of hashing.

What is rehashing in collision?

Rehashing is a collision resolution technique which tries to find another empty spot for the value that causes collision. It is a process through which of the table is doubled and the value that causes collision can find the spot in that new table.

What is the difference between double hashing and rehashing?

In double hashing, two different hash functions are applied at the same time and in rehashing same function is applied again and again to generate a unique mapping value.

Conclusion

I hope you have got a hold of these new topics, and you must be thrilled about learning something new. But learning never stops, and a good coder should keep practicing no matter what. So head over to our practice platform Coding Ninjas Studio to practice top problems, mock tests, and many more. To learn more about Data Structures and Algorithms, you can enroll in our course on DSA in Java.