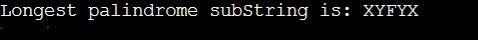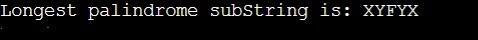APPROACH 2:
We can use the Dynamic Programming approach to solve the longest palindromic substring problem.
We will make a 2D D.P. table and we will store the answer for all (i, j) pairs so that we don’t need to compute the answer for the already computed (i, j) pairs. Dp[i][j] will be 0 if the substring(i, j) is not palindrome, else it will contain its length. We will first consider all the 1 sized substrings then using the result of the 1 sized substrings we will compute the answer for the 2 sized substrings and similarly till the n sized substring.
import java.util.*;
class Main {
public static String longestPalSubstr(String S) {
char s[] = S.toCharArray();
int n = s.length;
//Creating a D.P. table
int dp[][] = new int[n][n];
int max = 0, x = 0, y = 0;
for(int g = 0; g < n; g++){
for(int i = 0, j = i + g; j < n; j++, i++){
if(g == 0) {
dp[i][j] = 1;
}
else if(g == 1){
/*
If s[i] == s[j] then only
the substring s(i, j) is palindrome.
*/
if(s[i] == s[j]) dp[i][j] = 2;
}
else{
/*
Current substring S(i, j) is
palindrome only if s[i] == s[j] and
the substring s(i+1, j-1) is palindrome.
*/
if(s[i] == s[j] && dp[i + 1][j - 1] != 0){
dp[i][j] = 2 + dp[i + 1][j - 1];
}
}
/*
If the Substring s(i, j) is the
longest palindromic substring
update the value of max
*/
if(dp[i][j] > max){
max = dp[i][j];
x = i;
y = j;
}
}
}
//Forming the longest palindromic substring
StringBuilder ret = new StringBuilder();
for(int i = x; i <= y; i++) {
ret.append(s[i] + "");
}
return ret.toString();
}
public static void main (String[] args) {
String str = "ZXYFYXAC";
System.out.print("Longest palindromic substring is: "+longestPalSubstr(str));
}
}
Output:
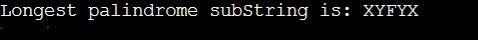
Time Complexity: The time complexity for the above code is O(N * N) because we are running 2 nested for loops of O(N).
Space Complexity: The space complexity for the above code is O(N * N) because we are maintaining a 2D D.P. table.
Also check out - Substr C++
APPROACH 3:
We can optimize Approach 2 for space complexity as follows:-
- The idea is to generate all the even length and the odd length palindromes and keep the track of the longest palindromic substring seen so far.
- To generate the odd length palindrome, Fix a center and expand in both directions for longer palindromes, i.e. fix the i (index) pointer as the center and two indices, i1 = i + 1 and i2 = i - 1
- Compare i1 and i2. If they are equal then decrease the i2 pointer and increase the i1 pointer and find the maximum length.
- Use a similar technique to find the even-length palindromic substring.
- Take the two indices i1 = i and i2 = i - 1 and compare the characters at the i1 and i2 index and find the maximum length till all pairs of compared characters are equal and store the maximum length.
- Return the maximum length.
public class Solution {
private int lo, maxLen;
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2){
return s;
}
for (int i = 0; i < len-1; i++) {
//assume odd length, try to extend Palindrome as possible
extendPalindrome(s, i, i);
//assume even length.
extendPalindrome(s, i, i+1);
}
return s.substring(lo, lo + maxLen);
}
private void extendPalindrome(String s, int j, int k) {
while (j >= 0 && k < s.length() && s.charAt(j) == s.charAt(k))
{
j--;
k++;
}
if (maxLen < k - j - 1) {
lo = j + 1;
maxLen = k - j - 1;
}
}
}
Output:
Time Complexity: The time complexity for the above code is O(N * N) because we are fixing the middle position ‘i’ and then calling extendPalindrome() function which runs in o(N) time.
Space Complexity: The space complexity for the above code is O(1) because we are using constant auxiliary space
Approach 4:
You can even solve this question in Linear Time Complexity(O(N)). There is one pre-designed algorithm, Manacher's Algorithm which can solve this problem in O(N) time. You can learn more about this algorithm here.
However, it is a non-trivial algorithm, and it’s very difficult to come up with that algorithm in a coding interview.
You can also read about Palindrome Number in Python here.
FAQs:
1. What optimization did we do on the recursive approach for the Longest Palindromic Substring problem?
- Since we were computing the answer for the same state at different times, we made a DP table to store the answer for the states we already computed, so that if in the future we need the answer for the same state we can directly return the answer from the DP table. Further, we saw how we can optimize it more so that our space complexity gets reduced to O(1).
2. What is the time complexity for the optimized approach?
- The time complexity for the optimized approach-2 is O(N * N) because we are storing the answer for all possible ‘i’ and ‘j’ pairs, and if we have already calculated the answer for any recursion call we return its answer stores in the DP table. And in approach-3 again we are taking O(N * N) time only.
Key Takeaways:
In this blog we have covered the following things:
- We first discussed the Recursive approach to solve this problem.
- Then we saw how we optimized the approach by memoizing using the DP table.
- In the end, we saw how we can optimize it more so that our space complexity gets reduced to O(1).
Check out this problem - Longest Subarray With Sum K
If you want to learn more about Dynamic Programming and want to practice some questions which require you to take your basic knowledge on Dynamic Programming a notch higher, then you can visit our Guided Path for Dynamic Programming. To practice this problem you can visit Practice Problem.
Until then, All the best for your future endeavors, and Keep Coding.