Lowest Common Ancestor in a Binary Search Tree

Introduction

In this blog, we will discuss a binary search tree problem that has been asked frequently in Interviews and also is one of the most important sets of binary search tree algorithms.

The problem is to find the Lowest Common Ancestor in a Binary Search Tree.

A common prerequisite before any BST problem is the knowledge of recursion because, without understanding recursion, things can become very difficult for you to understand. Before we proceed, we must know what a Binary Search Tree is.

A Binary Search Tree is a binary tree that follows a special property that any node in the left subtree in the BST is smaller than the root node and any node in the right subtree in the BST is greater than the root node. Every subtree of the BST must follow this property,

Also see, Data Structures

Let’s look at the problem first.

We are given a reference or a pointer to the root of a binary search tree. Now our task is to find the Lowest Common Ancestor in a Binary Search Tree.

Let’s understand the Lowest Common Ancestor’s definition.

Let a and b be two nodes present in a binary search tree. Then, LCA is defined as the lowest node in the binary search tree, whose descendants are a and b, respectively.

Also see, Difference Between Binary Tree and Binary Search Tree

Note: A node is a descendant of itself.

Given a binary Search tree,

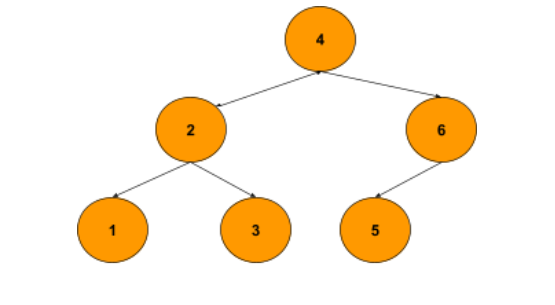
Input: reference/pointer to nodes 3 and 1.

Output: reference/pointer to node 2.

What are the common ancestors of nodes 3 and 1? They are nodes 4 and 2.

Now, by definition, out of nodes 4 and 2, which one is the lowest node?

The answer is Node 2. Hence the LCA of nodes 3 and 1 is node 2.

Let’s look at the approach to this question.

Must Read Recursive Binary Search.

Approach

Try recalling how to find the Lowest Common Ancestor of a Binary Tree. Then, you will get a sense of approaching this problem, and you will notice that special property followed by any BST makes the problem much more trivial than finding the LCA in a binary tree of 2 given nodes.

Let’s discuss some ideas.

Notice how we traverse down the tree to reach both the nodes; if both of them are smaller than the root node, we move to the left, and if they both are greater than the root node, we will go on the right.
But how do we traverse when we have one of the values smaller than the root node and the other greater than the root node?

If one tends to observe in case b), when we reach the LCA, it will segregate the 2 nodes in the left and the right subtree. Hence, we encounter this case, we can declare the root node of the subtree as the Lowest Common Ancestor of a Binary Search Tree.

See the below example to visualize the above case where we want to find the LCA of 1 and 3.

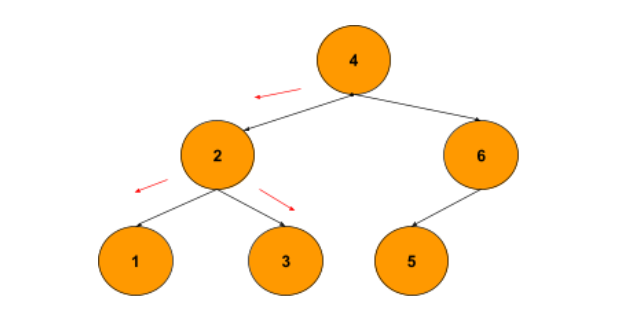
When we start traversing from root node 4 we see that nodes 1 and 3 lie in the same subtree but when we reach node 2, we see that nodes 1 and 3 now lie in different subtrees. Hence we declare node 2 as the LCA.

Another case we might encounter is if one of the given 2 nodes occurs before the other and the other node lies in its left or right subtree, then the node which occurs first is our LCA.

(NOTE: this is a case that has been discussed separately so that we don’t miss out on any case, but it will be handled by the case (b) discussed before this case (Why?) since out of the 2 nodes, the node that occurred first will split both nodes into different subtrees. Hence the node occurring first will be our LCA).

So approach can be formulated as:

If both given nodes are smaller than the root node, traverse the left subtree.
If both given nodes are greater than the root node, traverse the right subtree.
If cases (1) and (2) don’t satisfy, return the current subtree root node.

PseudoCode

Algorithm

___________________________________________________________________

procedure findLCAinBST( rootNode, nodeA, nodeB ):

___________________________________________________________________

1. If rootNode is NIL do # base case

2. return rootNode

3. end if

4. if nodeA.data < rootNode.data and nodeB.data < rootNode.data do

5. return findLCAinBST(rootNode.left, nodeA, nodeB)

6. end if

7. if nodeA.data > rootNode.data and nodeB.data > rootNode.data do

8. return findLCAinBST(rootNode.right, nodeA, nodeB)

9. end if

10. else do

11. return rootNode

12. end procedure

___________________________________________________________________

CODE IN C++

Now, let’s have a look at the Lowest Common Ancestor in a Binary Search Tree:

//C++ program to find the Lowest Common Ancestor of 2 nodes in a BST

#include <bits/stdc++.h>

using namespace std;



// struct Node to create Nodes in the Binary search tree

struct Node{

    int data;    // value of the node

    Node *left;  // left child

    Node *right; // right child

    Node(int d)

    {

        this->data = d;

        this->left = nullptr;

        this->right = nullptr;

    }

};

// function that finds the LCA of given 2 nodes present in the binary search tree

Node* findLCAinBST(Node* root, Node *nodeA, Node *nodeB){

    if(root==nullptr)   // base case

        return root;

    // if both nodes a and b are smaller than root node

    if(nodeA->data < root->data and nodeB->data < root->data)

        return findLCAinBST(root->left, nodeA, nodeB);   // go to the left subtree

    

    // if both nodes a and b are greater than root node

    if(nodeA->data > root->data and nodeB->data > root->data)

        return findLCAinBST(root->right, nodeA, nodeB);  // go to the right subtree

    

    // return the root since this is the LCA

    return root;

}

int main(){

    // size of the binary search tree

    int size = 6;

    // creating a sample binary search tree

    Node *root = new Node(4);

    root->left = new Node(2);

    root->right = new Node(6);

    root->right->left = new Node(5);

    root->left->left = new Node(1);

    root->left->right = new Node(3);

    // find the pointer to the LCA node for the nodes with value 1 and 3.

    Node *LCA = findLCAinBST(root, root->left->left, root->left->right);

    cout<<"The lowest common ancestor of the given node A and node B is: "<<LCA->data;

    return 0;

}

You can also try this code with Online C++ Compiler

Run Code

Output

The lowest common ancestor of the given node A and node B is: 2

Time Complexity: O(h)

The above algorithm takes O(h) time complexity, where h is the height of the binary search tree. We traverse the binary search tree along with its height, and the maximum we can go up is till we reach its height.

Space complexity: O(h) at the worst case, as we are recursively traversing the BST.

Frequently Asked Questions

How to find a sum in a Binary Search tree?

We can write a recursive solution that returns the sum of the root, the sum of the nodes of the left subtree, and the sum of the nodes of the right subtree.

Why does Inorder traversal on a BST return the sorted value of the nodes?

It’s because, in an inorder traversal, we visit the left subtree first, then the root, and finally the right subtree. So if we try to write inOrder traversal in a recursive manner then we can say that, inOrder traversal = {(left subtree values), root, (right subtree values)}. Now all values to the left of the root in the order are smaller and all values to the right of the root are greater than it. This is the property that a sorted order also follows.

What is the searching time complexity in a BST?

On average, the worst-case time complexity is O(Logn), and in the worst case, it’s O(n), i.e., the case of a skewed BST where ‘n’ is the number of nodes in the BST.

Conclusion

This article taught us how to find the Lowest Common Ancestor in a Binary Search Tree by approaching the problem using a recursive approach. We discussed its implementation using a recursive method using illustrations, pseudocode, and then proper code.

We hope you could take away critical techniques like analyzing problems by walking over the execution of the examples and finding out the recursive pattern followed in most binary search tree problems.