Introduction
In this blog, we will try to understand a very interesting problem of a Binary Tree data structure in which we will find the Lowest Common Ancestor of any two given nodes of that binary tree using RMQ. Through that problem, we will learn how to approach any such problem. Firstly, we will look into the problem statement, get some knowledge about Binary tree data structure, decide what will be the optimal approach, and then we will proceed towards the implementation in any of the programming languages.
What is a Binary Tree?
A Binary Tree is a type of tree data structure in which elements have the utmost two children nodes. Since, in this data structure, elements have only two children nodes, we name them the left child and the right child.
Any node of Binary contains the following information. These are:
- Its data
- Pointer to its left child.
- Pointer to its right child.
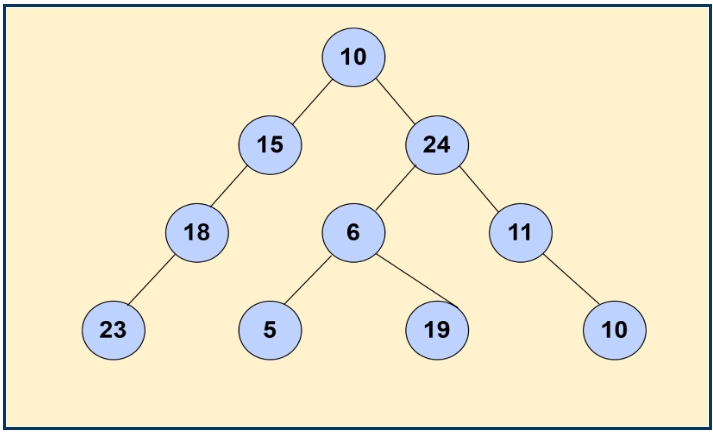
For Example, if we consider the tree above, 10 is the root node, and the rest of the nodes are its children nodes. We pick any node, say 6, so, 5 will be its left child and 19 will be its right child. That is, 6 is the parent node to children nodes 5 and 19.
Problem Statement
Firstly, we will have a look at what exactly the problem says.
We are given a binary tree that has n nodes. We have to find the lowest common ancestor of any two given nodes of that binary tree using RMQ. By lowest common ancestor, we mean that parent node which is the lowest and is common to both of the given nodes.
RMQ stands for Range Minimum Query. RMQ is used to find out the position of the element whose value is minimum between the two mentioned indices. There are three approaches for solving RMQ, namely, Brute force, Square Root Decomposition, and Segment Tree Approach with different time and space complexities. Since we find that the Segment Tree Approach is the most optimal one, we will use that approach here.
Here, we are assuming that all the values inside the nodes are positive.
Sample Examples
Let us understand the above-mentioned concepts, which are, Lowest Common Ancestor and Range Minimum Query with the help of examples.
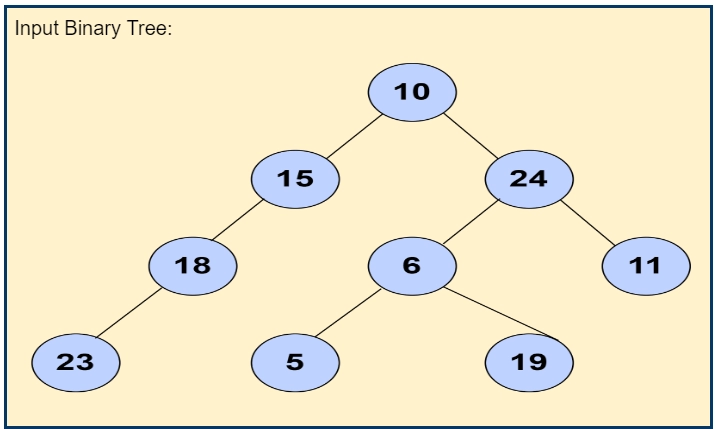
Suppose that we have a binary tree as you can see in the image below. We have to search for the lowest common ancestor of the two given nodes of that binary tree. We will use the same binary tree for different examples to have a better grab of all the possible cases.
Example 1:

Explanation:
In the above example, we can see a binary tree. Firstly, we will search for both the input nodes, which are, 5 and 9. As soon as we get the nodes, we will traverse up to find all the ancestors of both the nodes and then determine which one is common to both and the lowest. Now, that be can see that 5 and 19 are children of the same node with value 6, and also, both the input nodes are at the same level. In this case, the output will be 6.
Example 2:

Explanation:
In the above example, we can see a binary tree. Firstly, we will search for both the input nodes, which are 5 and 24. As soon as we get the nodes, we will traverse up to find all the ancestors of both the nodes and then determine which one is common to both and the lowest. Now, that be can see that 5 and 24 appear on the right side of the root node but are at different levels. The lowest common ancestor we observe in this case is 24.
Example 3:

Explanation:
In the above example, we can see a binary tree. Firstly, we will search for both the input nodes, which are 18 and 24. As soon as we get the nodes, we will traverse up to find all the ancestors of both the nodes and then determine which one is common to both and the lowest. Now, that be can see that 18 and 24 appear at the different sides of the root node and also are at different levels. The lowest common ancestor we observe in this case is the root node itself, that is, 10.
Approach
For this problem, firstly, our approach is to traverse the tree using Euler’s tour method.
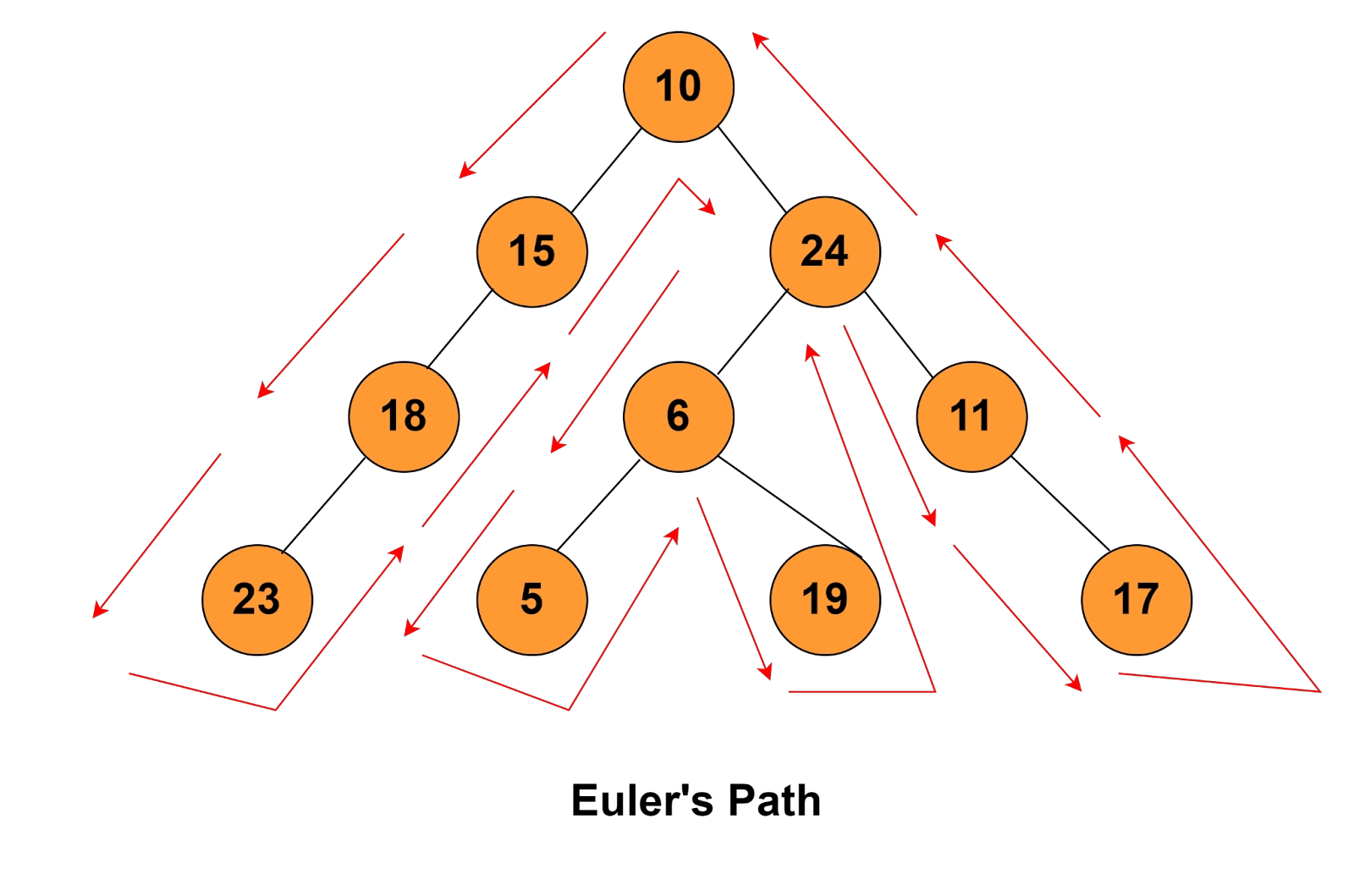
We will use two arrays also. The first array will be used to store the nodes coming in the path while traversing and the second node will be used to store their corresponding levels.
Euler’s Path:

Corresponding levels:

As soon as we get the input two nodes for which we need to find the lowest common ancestor, we will search them in the first array and mark their first occurrence. Let's say we took 15 and 6 as the input nodes.

Now we will mark the same indices in the second array.

We observe that there are three elements between the two marked boxes, that is, 2, 3, and 0. The smallest of all three is 0. Now, that we know 0 is the smallest corresponding level. We will refer to the first array and find what value exists corresponding to 0, that is 10. So, the output will be 10.
PseudoCode
//Function to find Lowest Common Ancestor
int searchLCA(TreeNode node, int n1, int n2)
{
Arrays.fill(first, -1);
entry = 0;
Tour(parent, 0);
obj.segment_tree = constructST(cl, 2 * n2 - 1);
if (first[n1] > first[n2])
n1 = swapping(n1, n1 = n2);
int a = first[n1];
int b = first[n2];
int index = RMQ(obj, 2 * n2 - 1, a, b);
return euler_path[index];
}Implementation in Java
import java.util.*;
class Segment
{
int segment_tree;
int segment_array[] = new int[1000];
}
class TreeNode
{
TreeNode l, r;
int value;
TreeNode(int number)
{
value= number;
l = r = null;
}
}
class Main
{
TreeNode parent;
int n2 = 9; // v is the highest value of node in our tree
int euler_path[] = new int[2 * n2 - 1];
int cl[] = new int[2 * n2 - 1];
int first[] = new int[2 * n2 - 1];
int entry;
Segment obj = new Segment();
// Driver program
public static void main(String args[])
{
Main tree = new Main();
tree.parent = new TreeNode(8);
tree.parent.l = new TreeNode(2);
tree.parent.r = new TreeNode(5);
tree.parent.l.l = new TreeNode(4);
tree.parent.l.r = new TreeNode(6);
tree.parent.r.l = new TreeNode(9);
tree.parent.r.r = new TreeNode(7);
tree.parent.l.r.l = new TreeNode(1);
tree.parent.l.r.r = new TreeNode(3);
int n1 = 4, n2 = 9;
System.out.println(tree.searchLCA(tree.parent, n1, n2));
}
int swapping(int val1, int val2)
{
return val1;
}
int Log2(int num1)
{
int result = 0;
int num2 = num1 >>= 1;
while (num2-- != 0)
result++;
return result;
}
// Euler Path of Tree
void Tour(TreeNode node, int l)
{
if (node != null)
{
euler_path[entry] = node.value;
cl[entry] = l;
entry++;
if (first[node.value] == -1)
first[node.value] = entry - 1;
if (node.l != null)
{
Tour(node.l, l + 1);
euler_path[entry] = node.value;
cl[entry] = l;
entry++;
}
if (node.r != null)
{
Tour(node.r, l + 1);
euler_path[entry] = node.value;
cl[entry] = l;
entry++;
}
}
}
//To construct segment tree
int constructST(int array[], int n)
{
int x = Log2(n) + 1;
int max_size = 2 * (1 << x) - 1;
obj.segment_array = new int[max_size];
make_segment(0, 0, n - 1, array, obj);
return obj.segment_tree;
}
//Function to implement RMQ
int RMQ(int position, int s1, int s2, int a, int b, Segment segment_tree)
{
//conditions for RMQ
if (a <= s1 && b >= s2)
return segment_tree.segment_array[position];
else if (s2 < a || s1 > b)
return -1;
int middle = (s1 + s2) / 2;
int c = RMQ(2 * position + 1, s1, middle, a, b, segment_tree);
int d = RMQ(2 * position + 2, middle + 1, s2, a, b, segment_tree);
if (c == -1)
return d;
else if (d == -1)
return c;
return (cl[c] < cl[d]) ? c : d;
}
// Uses RMQ function to return minimum of elements between indices a and b
int RMQ(Segment segment_tree, int n, int a, int b)
{
if (a < 0 || b > n - 1 || a > b)
{
System.out.println("Invalid input");
return -1;
}
return RMQ(0, 0, n - 1, a, b, segment_tree);
}
//Recursive function to construct Segment Tree
void make_segment(int si, int s1, int s2, int arr[], Segment segment_tree)
{
if (s1 == s2)
segment_tree.segment_array[si] = s1;
else
{
int middle = (s1 + s2) / 2;
make_segment(si * 2 + 1, s1, middle, arr, segment_tree);
make_segment(si * 2 + 2, middle + 1, s2, arr, segment_tree);
if (arr[segment_tree.segment_array[2 * si + 1]] < arr[segment_tree.segment_array[2 * si + 2]])
segment_tree.segment_array[si] = segment_tree.segment_array[2 * si + 1];
else
segment_tree.segment_array[si] = segment_tree.segment_array[2 * si + 2];
}
}
//Function to find Lowest Common Ancestor
int searchLCA(TreeNode node, int n1, int n2)
{
Arrays.fill(first, -1);
entry = 0;
Tour(parent, 0);
obj.segment_tree = constructST(cl, 2 * n2 - 1);
if (first[n1] > first[n2])
n1 = swapping(n1, n1 = n2);
int a = first[n1];
int b = first[n2];
int index = RMQ(obj, 2 * n2 - 1, a, b);
return euler_path[index];
}
}
Input:
n1=4, n2=9
Output:
8
Complexity Analysis
Time Complexity
- For Euler’s path, if the number of nodes is ‘n’. Then, the resultant complexity will be O(n).
- For the construction of the Segment Tree, the complexity will be O(n).
- For RMQ, the complexity will be O(log n).
So, we conclude that the overall complexity for the implementation above is O(log n).
Space Complexity
We observe that extra auxiliary space is required in various instances. Hence, the resultant space complexity will be O(n).





