Introduction
Reinforcement learning is an area of Machine Learning. It enables machines and software agents to automatically select the best behavior in a given situation to improve their efficiency. For the agent to learn its behavior, simple reward feedback is required, known as the reinforcement signal.
Many different algorithms address this problem. A specific type of problem characterizes reinforcement Learning, and all solutions to that problem are classified as Reinforcement Learning algorithms. An agent is meant to choose the best action based on his present state in the situation. The problem becomes a Markov Decision Process when this phase is repeated.
Markov Decision Process (MDP)
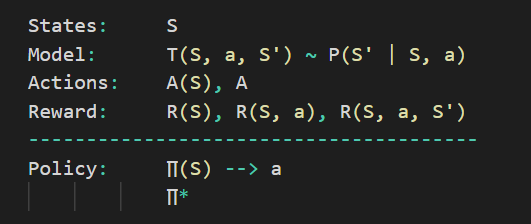
A Markov decision process includes:
- A collection of potential world states S.
- A collection of Models.
- A list of possible actions A.
- Reward function R(s, a).
-
A policy.
State
A state is a collection of tokens that represent every possible state for the agent.
Model
A Model (also known as a Transition Model) describes how an action affects a state. T(S, a, S') specifies a transition T that occurs when we are in state S and do action 'a', resulting in state S' (S and S' may be the same). We also construct a probability P(S'|S, a) for stochastic actions (noisy, non-deterministic), which is the chance of reaching a state S' if action 'a' is conducted in state S.
The Markov property asserts that the results of an action made in a state are solely determined by that state and not by the previous history.
Actions
A course of action A is a collection of all actions that can be taken. The set of actions that can be taken while in state S is defined by A(s).
Reward
A Reward is a reward function with a real value. The reward for simply being in the state S is R(s). The reward for being in state S and doing action 'a' is R(S, a). The reward for being in state S, taking action 'a', and ending in state S' is R(S, a, S').
Policy
A policy is a Markov Decision Process solution. A mapping from S to 'a' is referred to as a policy. It specifies the 'a' action to be performed while in state S.
3 |
🎁 |
|||
2 |
☠☠☠ |
🔥🔥 |
||
1 |
Start |
👷♂️ |
||
1 |
2 |
3 |
4 |
Consider the above grid example.
Agent lives in the cell(1, 3). A 3*4 grid is used in this example. A START state exists in the grid (cell 1,1). The agent's mission is to make his way around the grid until he finds the Gift (cell 4,3). The agent should stay away from the Fire grid at all times (orange color, cell 4,2). In addition, grid no. 2,2 is a blocked grid that works as a barrier, preventing the agent from entering.
Any of the following actions are available to the agent: L(left), R(right), U(up), D(down)
Walls obstruct the agent's path; if a wall is in the way of the agent's path, the agent remains in the same spot. If the agent, for example, says L in the START grid, he will remain in the START grid.
Objective: To discover the shortest path from START to the Gift.
There are two such paths : (R, R, U, U, R) and (U, U, R, R, R). Let’s consider the first one. This move is now noisy. The targeted action is successful 80 percent of the time. The action agent will move at right angles 20% of the time. If the agent says UP, the chance of traveling U is 0.8, 0.1 for going L, and 0.1 for traveling R (since L and R are right angles to U).
Each time the agent takes a step, it is rewarded with a little reward (can be negative when it can also be termed as punishment, in the above example, entering the Fire can have a bonus of -1). In the end, the agent is given big rewards (good or bad). The goal is to maximize the total sum of rewards.
Constrained Markov Decision Processes
CMDPs (Constrained Markov Decision Processes) are extensions to Markov Decision Process extensions (MDPs). There are three key distinctions between MDPs and CMDPs.
- Instead of a single cost, several expenses are incurred when an action is taken.
- Only linear programs are used to solve CMDPs, and dynamic programming is not an option.
- The final policy is determined by the initial state.




