Maximal Matching
If adding an edge in G but not in M makes M not a matching, the matching M of graph G is said to be maximal.
Put another way, a maximal matching M is not a proper subset of any other G matching. The graphs below, for example, represent maximal matchings -
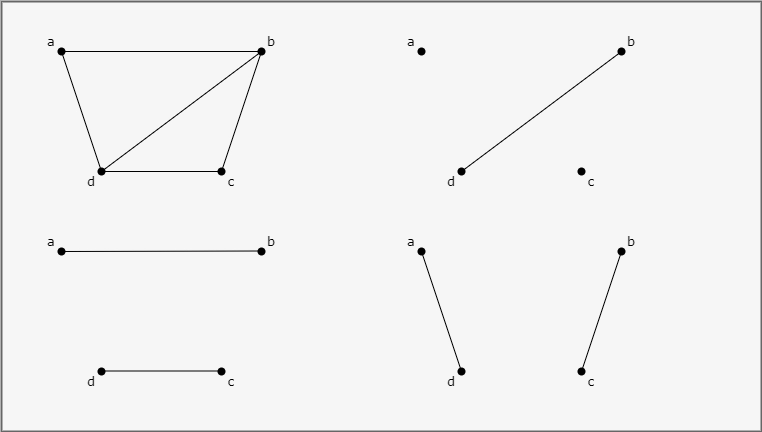
If any edge is added to any of the above graphs, they will no longer be a match.
Maximum Matching
If a matching M of graph G is maximal and has the most edges, it is said to be maximum.
A graph may have a large number of maximum matchings. Largest maximal matching is another name for it.
Although every maximum match is also a maximal match, not every maximal match is also a maximum match.
The matching number of 'G' is the number of edges in the maximum matching.
The image below shows an example of maximum matching.
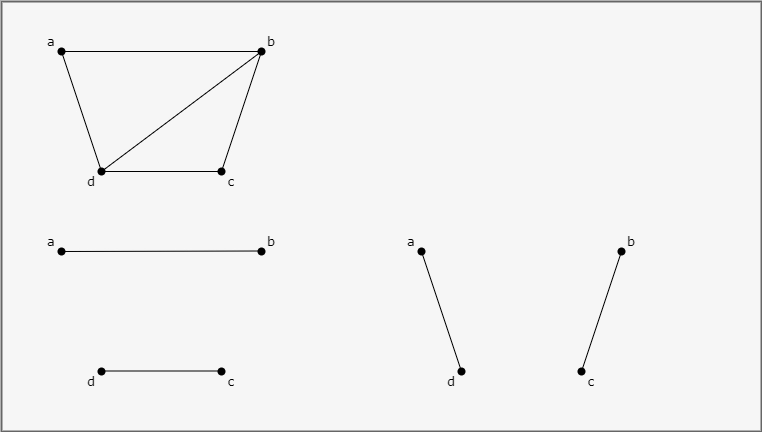
Perfect Matching
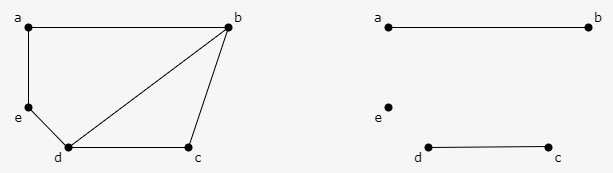
If every vertex is connected to precisely one edge, a matching M of graph G is said to be perfect. Although every perfect match is also a maximum match, not every maximum match is also a perfect match.
Each vertex in the subgraph should have a degree of 1. In other words,
deg(V) = 1 ∀ V
Every perfect graph matching is also a maximum graph matching because there is no way to add another edge to a perfect matching graph.

Because a perfect matching must contain every vertex, the number of edges in the matching must be |V|/2, where V is the number of vertices. As a result, a perfect match only exists when the number of vertices is even. Though, having an even number of vertices does not confirm that perfect matching exists for that graph.
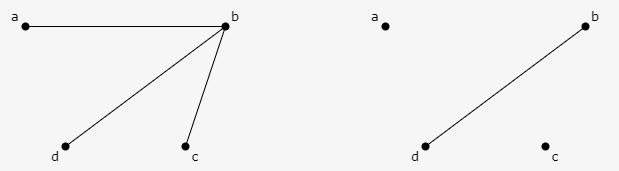
Near Perfect Matching
If the number of vertices in the original graph is odd, the last vertex couples with the other vertex, leaving just one vertex that cannot be coupled with any other vertex with a degree of zero. It violates the notion of perfect matching. It is considered to be near perfect.
Perfect Matching in a Complete Graph
The count of perfect matchings in a complete graph, Kn is calculated as follows.
The number of perfect matchings is 0 if the number of vertices in the graph is odd, i.e. n is odd.
However, if n is even, we may calculate the number of perfect matches using a general method.
We can denote n as 2m, where m is any positive integer because n is even.
In a perfect network, every vertex is connected to every other vertex; hence each vertex's degree is 2m-1. We must choose one of these 2m-1 edges to include two vertices.
We can select an edge in 2m-1 ways. Because the edges connecting to the already picked vertices cannot be chosen because it is a matching, 2m-2 vertices and (2m-2)-1 = 2m-3 edges remain.
So there are 2m-3 methods to choose an edge from 2m-3 edges. We can continue to select edges in the same manner, then apply the product rule-
Number of perfect matchings = (2m-1) * (2m-3) *...*3*1
It's also possible to write it like this:
= {(2m-1) * (2m-3) *.....*3*1} * {(2m) * (2m-2) * (2m-4) * ..... * 4 * 2} / {(2m) * (2m-2) * (2m-4) * ..... * 4 * 2}
= (2m)! / { 2m * (m) * (m-1) * ..... * 2 * 1 }
= (2m)! / 2m * m!
The number of perfect matchings for a perfect graph with 2m vertices is (2m)! / 2m * m!.
Bipartite Matching
In a Bipartite Graph, a matching is a group of edges chosen so that no two edges share an endpoint. A maximum match is a match that is the largest possible (maximum number of edges). If any edge is added to a maximum matching, it is no longer a matching. For a given Bipartite Graph, there can be several maximum matchings.
Flow networks, scheduling, and planning, graph colouring, and neural networks are just a few of the uses of matching. The scheduling problem, in which there are m jobs that can be accomplished by n workers, is the most common. Tasks and workers are the two sets of vertices in a bipartite graph, with a task being connected to a worker if that worker can accomplish it.
Thus, the problem is to find a maximum matching.
To learn more about Bipartite graph and matching, follow the link Bipartite Graph - Coding Ninjas Coding Ninjas Studio and Bipartite Graph.
FAQs
-
What is a graph?
A graph is a structure consisting of a collection of elements, some of which are "connected" in some way. The graph's objects are called vertices, and the connections between them are called edges. A graph is shown as a series of dots representing vertices connected by lines or curves representing edges.
Formally, "A graph G = (V, E) is made up of V, which is a non-empty set of vertices (or nodes), and E, which is a collection of edges. Each edge has one or two endpoints, which are the vertices associated with it."
-
Briefly describe the Graph Theory.
Graph theory is a branch of mathematics and computer science that studies the relationship between edges and vertices in graphs. It is a widely studied subject with applications in computer science, information technology, biosciences, mathematics, and linguistics, to name a few.
-
What is the primary difference between directed and undirected graphs?
A directed graph is one in which the edge direction is defined in relation to a specific node.
A graph in which the edge direction is not specified is known as an undirected graph. If node 'u' and 'v' are the vertices of an edge, then there is a path from node 'u' to 'v' and vice versa.
-
Define a complete graph.
A complete graph is a simple graph with n vertices and exactly one edge between each pair of vertices. Kn denotes a complete graph with n vertices. The total number of edges in the complete graph with n vertices is n*(n-1)/2.
Key Takeaways
In this article, we learnt about matching in Graph theory. We also learnt about Maximum matching, Maximal matching, Perfect matching and Bipartite matching.
We hope this blog has helped you enhance your knowledge. If you want to learn more, check out our articles on Graph | Learn & Practice from Coding Ninjas Studio, Graph Types and Applications - Coding Ninjas Coding Ninjas Studio and Graph Theory - Coding Ninjas Coding Ninjas Studio. Do upvote our blog to help other ninjas grow.
Head over to our practice platform Coding Ninjas Studio to practice top problems, attempt mock tests, read interview experiences, and much more!
Happy Reading!









