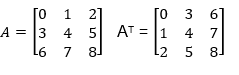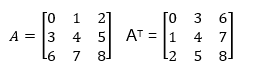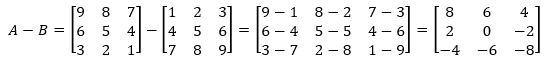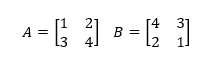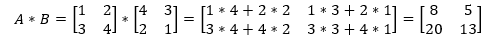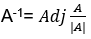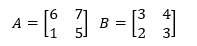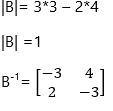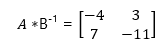Introduction
You have the arrays feature to store data in any row or column. Arrays can store data very efficiently, but imagine a case where you want to keep more than one array of the same size and access them together. Still, it is very difficult to manage so many arrays, so how can we solve this problem?
We can solve this problem using matrices as they are a collection of arrays of the same size. We will discuss the matrix in detail while moving further in the blog, so let's go on with our topic without wasting any time.
Matrix and Types
You can understand matrix as the set or collection of numbers arranged in vertical and horizontal lines. The vertical lines are called columns, and the horizontal lines are known as rows.
The values or numbers entered in the matrix are entries or elements.
It is represented inside a pair of square brackets [].
It can be referred to as the set of arrays. The matrix with n number of rows and m number of columns is called the n x m matrix. We use capital alphabets to represent the matrix with its element denoted in its subscript by small numbers.
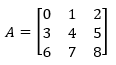
In the above image, we represented a 3 x 3 matrix. The total number of elements in the matrix is the number of elements in each row multiplied by the number of rows or the number of rows multiplied by the number of columns.
Types of Matrix
There are many types of matrices available we will discuss them here briefly.
- Empty Matrix: As the name suggests, it is an empty matrix. i.e., the matrix with no rows and no columns.
- Column Matrix: The matrix which contains only one column and more than one number of rows is called the column matrix.
- Row Matrix: The matrix which contains only one row and more than one number of columns is called the row matrix.
- Square Matrix: The matrix which contains the same number of rows and columns is called a square matrix.
- Diagonal Matrix: The matrix that contains only elements in its principal diagonal and all the other elements other than zero is called a diagonal matrix.
- Scalar Matrix: The matrix with all the principal diagonal elements equal is called the scalar matrix.
- Identity Matrix: The matrix with all principal diagonal elements as one and all the remaining elements as zero is called identity matrix or unit matrix.
- Triangular Matrix: The matrix that only has elements in triangular formation either above or below the principal diagonal is the triangular matrix.
- Submatrix: Although it is not a matrix type, we should know it. After removing a particular row or column from the matrix, it is part of the primary matrix that we get.